Du står overfor utfordringen med å effektivt identifisere trender i tidsserier? Da kan eksponentiell glatting være en metode som kan hjelpe deg med å lage mer nøyaktige prognoser. I denne veiledningen vil du lære trinn for trinn hvordan du utfører eksponentiell glatting i Excel for å analysere og visualisere trender i dataene. Vi vil sammen oppleve hvordan du oppnår meningsfulle resultater med minimal innsats.
Viktigste innsikter
- Eksponentiell glatting muliggjør en finjustering mot trendene i tidsserier.
- Bruk av en glattingsparameter (Alfa) på 0,15 for trendberegning.
- Beregning av svingningskomponenter og sesongmessige verdier for bedre analyse.
Trinnvis veiledning
Trinn 1: Forbered dataene
Først trenger du en tabell med relevante data som du ønsker å analysere. Du bør legge inn dataene i Excel, der datoene og tilhørende antall står i side om side kolonner. Kopier alle nødvendige verdier, spesielt overførbare datoer og antall. Disse verdiene er grunnlaget for analysen din.
Trinn 2: Fastsett glattingsparameter
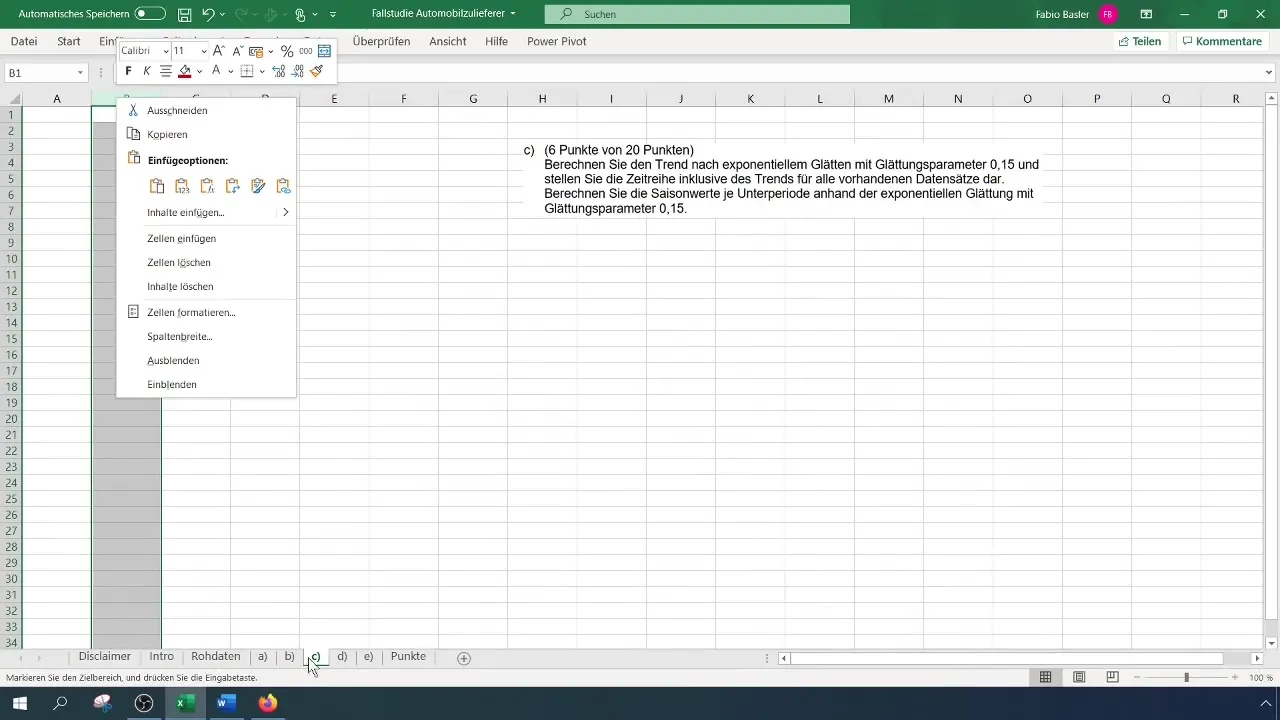
Før du begynner med eksponentiell glatting, må du fastsette glattingsparameteren. Dette er vanligvis en verdi mellom 0 og 1 som avgjør hvor mye de siste observasjonene veies. I dette tilfellet har vi valgt en alfaværdi på 0,15. Denne verdien er populær og effektiv i tidsserieanalyse da den verken fokuserer for mye på de nyeste verdiene eller er for konservativ.
Trinn 3: Utfør trendberegning
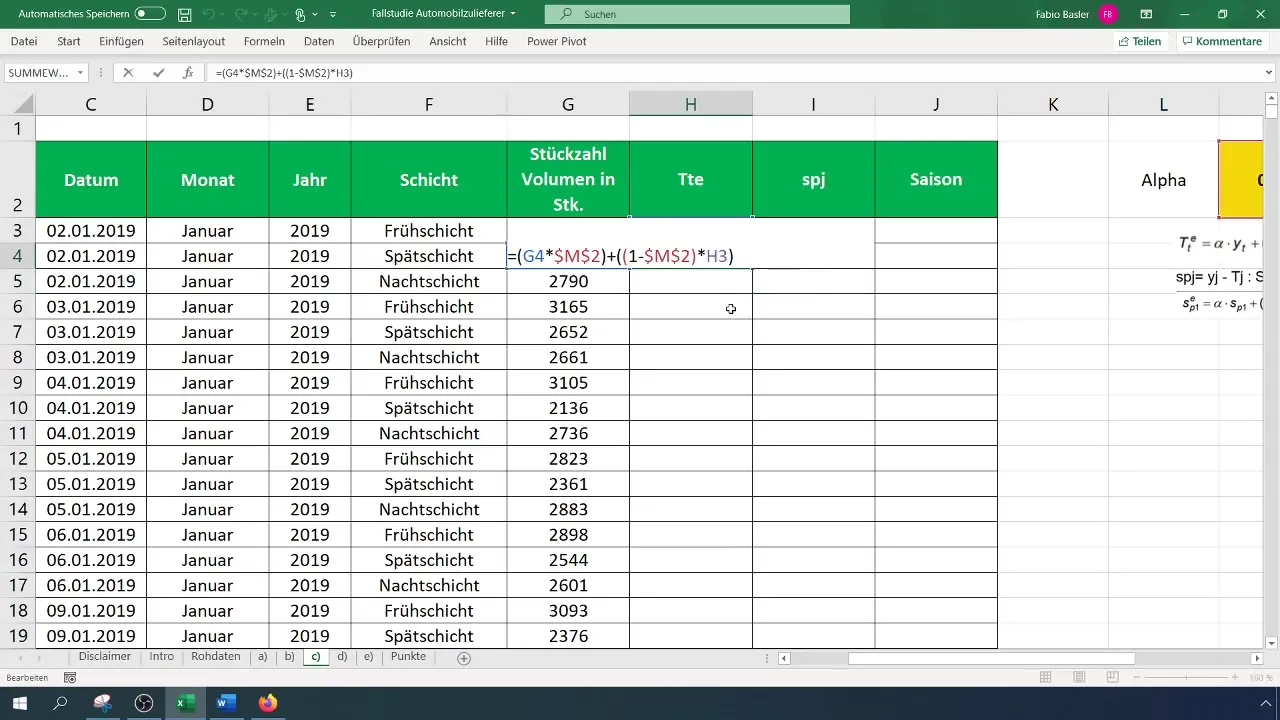
Neste element er å beregne trenden. Begynn med å skrive inn formelen for eksponentiell glatting i den tilsvarende cellen. Pass på å beholde den første observasjonen uendret. Fra og med den andre punktet blir formelen brukt ved å veie den sist beregnete trendverdien med alfaværdien. Innholdet i cellen din kan se slik ut:
[ T_t = \alpha \cdot Yt + (1 - \alpha) \cdot T{t-1} ]
Bruk denne formelen for å beregne den første trendverdien, og dra deretter formelen nedover for å finne de neste trendverdiene.
Trinn 4: Beregn svingningskomponenten
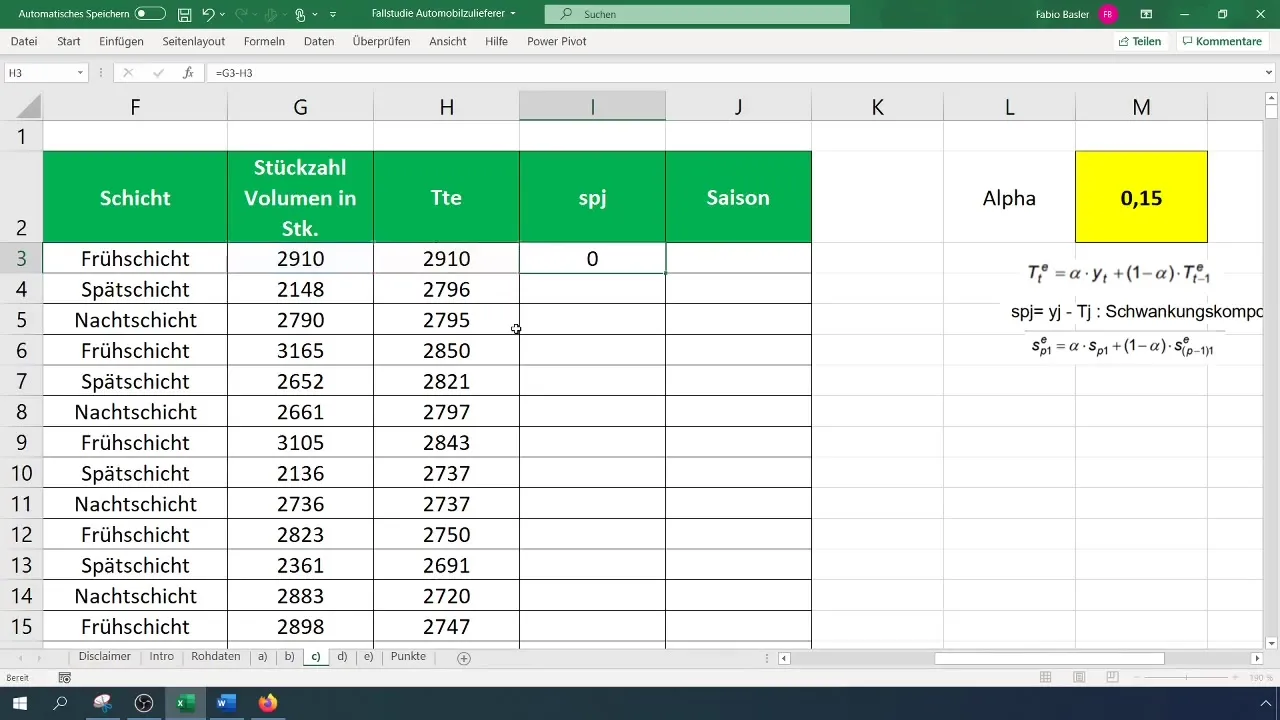
Etter trendberegningen er det på tide å finne svingningskomponenten. Dette gjøres enkelt ved å finne differansen mellom de faktiske verdiene og trendverdiene. Formelen for dette er:
[ S_j = Y_j - T_j ]
Husk å utføre denne beregningen for hvert datapunkt du analyserer.
Trinn 5: Identifiser sesongmessige verdier
Neste steg innebærer å identifisere de sesongmessige verdiene. Først må du finne antall underperioder i dataene dine. Her vil du oppdage at det vanligvis bør være en viss regelmessighet i dataene dine. Merk ned antall underperioder, da dette er essensielt for de sesongmessige beregningene.
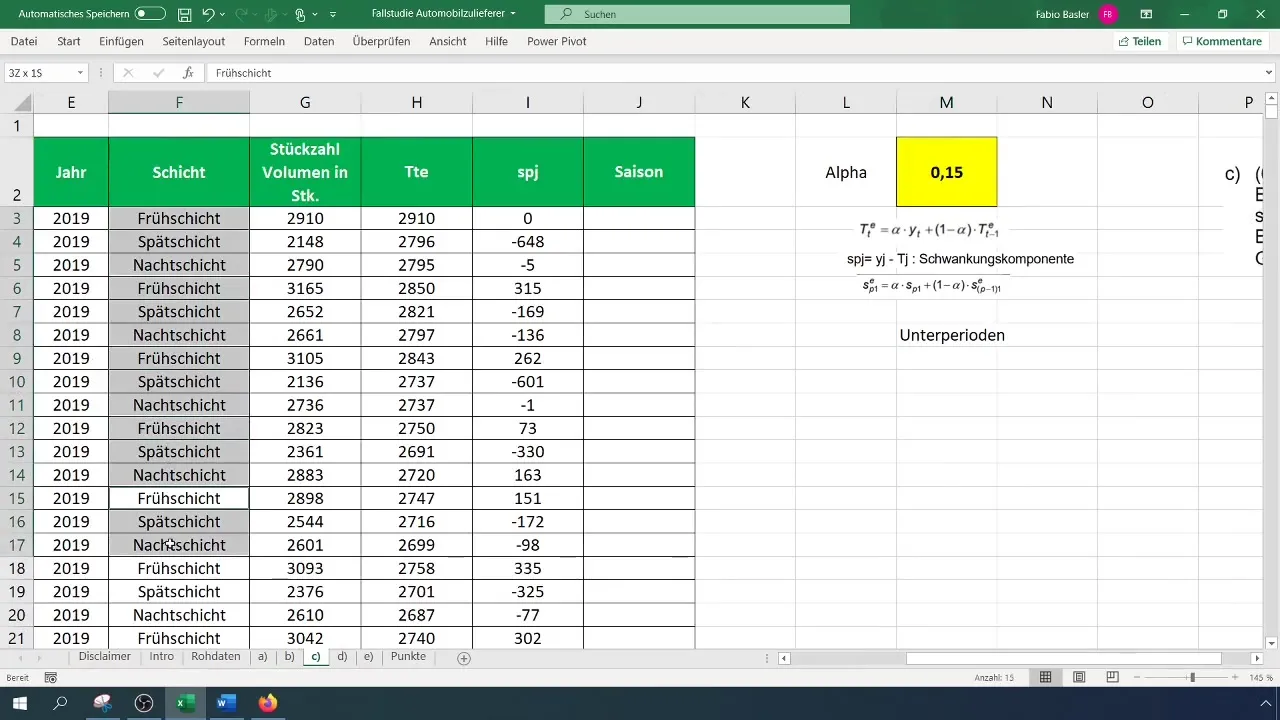
Nå som du trenger de sesongmessige verdiene, begynn med å kopiere de første observasjonene og gjøre beregningene for de sesongmessige verdiene fra den fjerde punktet ved å multiplisere de tidligere svingningene med alfa- og en motalfa-verdi (1 - alfa). Pass på å fikse formlene før du kopierer dem slik at du får resultatene for de følgende punktene.
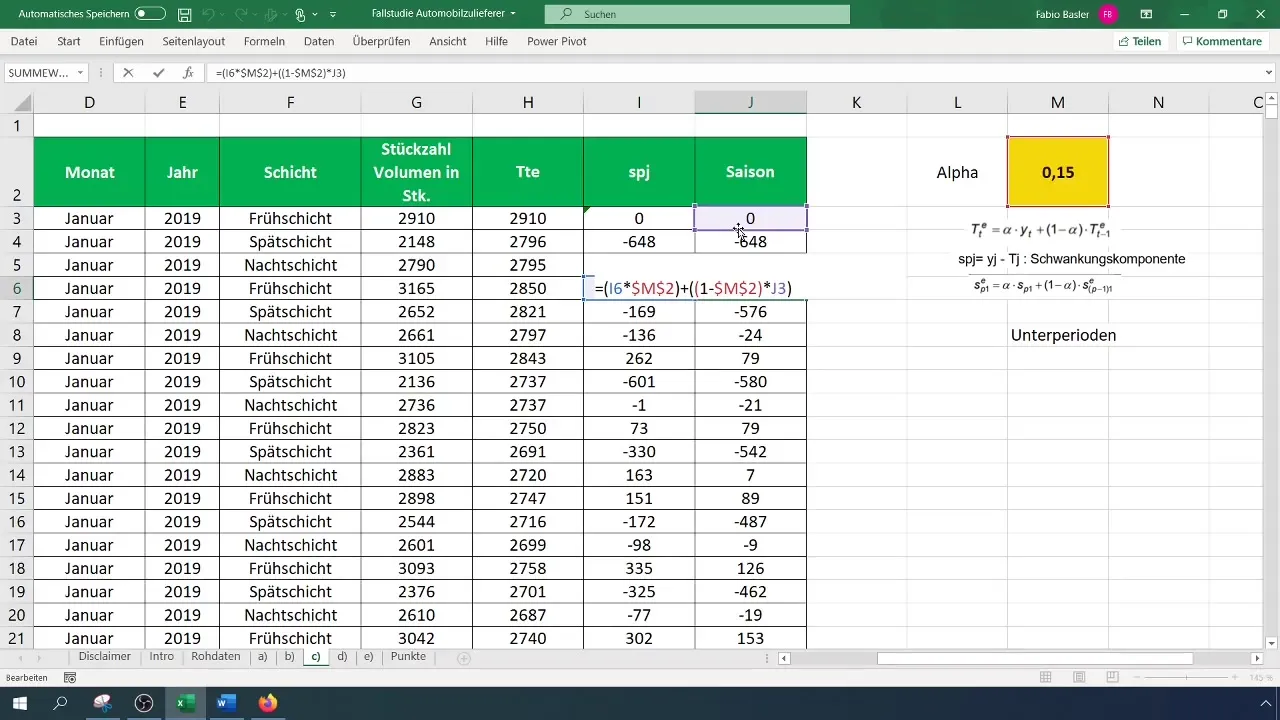
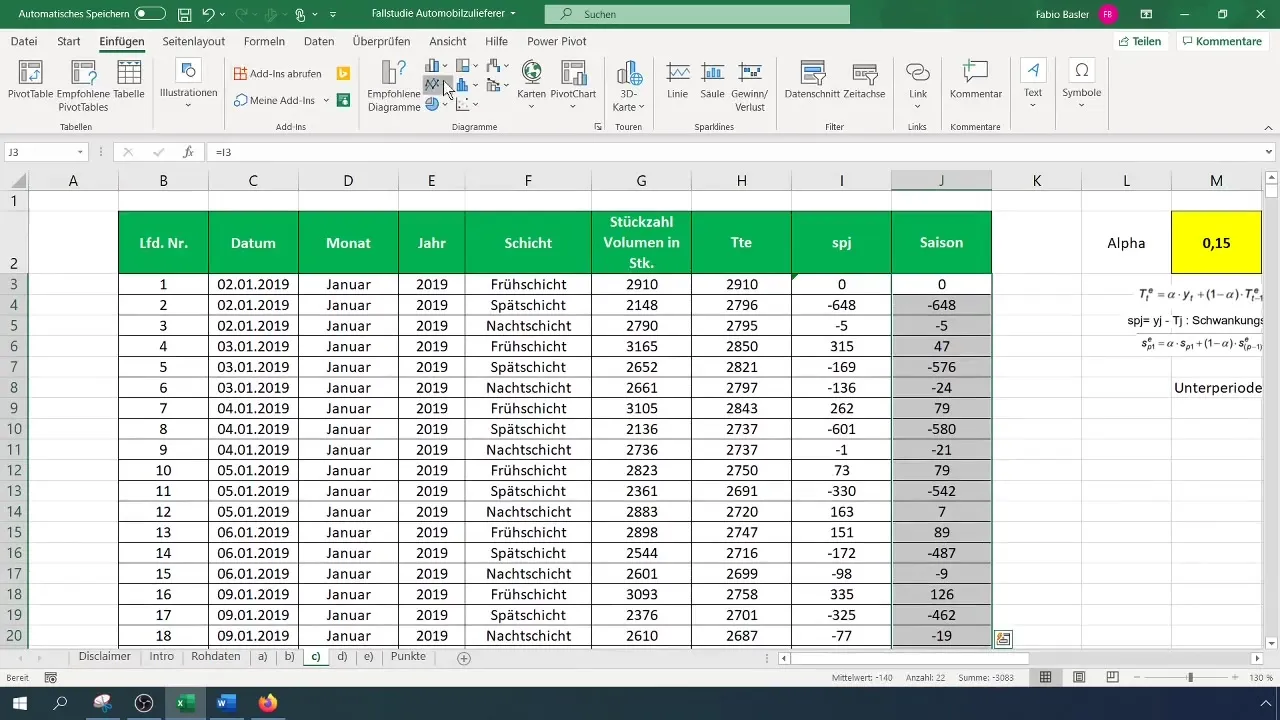
Trinn 6: Visualiser resultater
For bedre forståelse av innsiktene dine, er en grafisk representasjon nyttig. Visualiser de sesongmessige verdiene i et linjediagram for å oppdage trender og mulige sykliske mønstre. Du kan forbedre synligheten av dataene dine ved å fremheve verdiene for den første måneden.
Oppsummering
Du har nå lært grunnleggende om utførelsen av eksponentiell glatting i Excel. Fra datainntasting til beregning av trend og variasjon til sesonganalyse har du tatt i bruk et effektivt verktøy for å få verdifulle innsikter i tidsseriedata.
Ofte stilte spørsmål
Hvordan bruker jeg glattingsparameteren (alfa)?Glatteparameteren bør ligge mellom 0 og 1; en verdi på 0,15 er ofte anbefalt for tidsanalysene.
Hva er svingningskomponenten?Svingningskomponenten er differansen mellom den faktiske verdien og trendverdien.
Hvor mange underperioder bør jeg bruke?Antall underperioder avhenger av datastrukturen din; i dette eksempelet var det tre.
Kan jeg tilpasse og visualisere resultatene selv?Ja, du kan tilpasse resultatene dine når som helst og visualisere dem grafisk i Excel.


