Statistiske tester er en essensiell del av dataanalyse, spesielt når det gjelder å undersøke forskjeller mellom grupper. En velprøvd metode som ofte brukes i forskning og næringsliv, er to-utvalgs-F-testen. Denne veiledningen viser deg trinn for trinn hvordan du kan gjennomføre en slik test med Excel for å sammenligne variablene til to legemiddelselskaper med hensyn til deres forskningsuttak.
Viktigste innsikter
- Du lærer hvordan du kan sammenligne variansen til to grupper ved å bruke en F-test.
- Veiledningen inneholder detaljerte trinn for å gjennomføre testen i Excel, inkludert bruk av dataanalysefunksjonen.
- Til slutt vil du vite hvordan du tolker resultatene og hvilke konklusjoner du kan trekke.
Trinnvis veiledning
Trinn 1: Forberede data
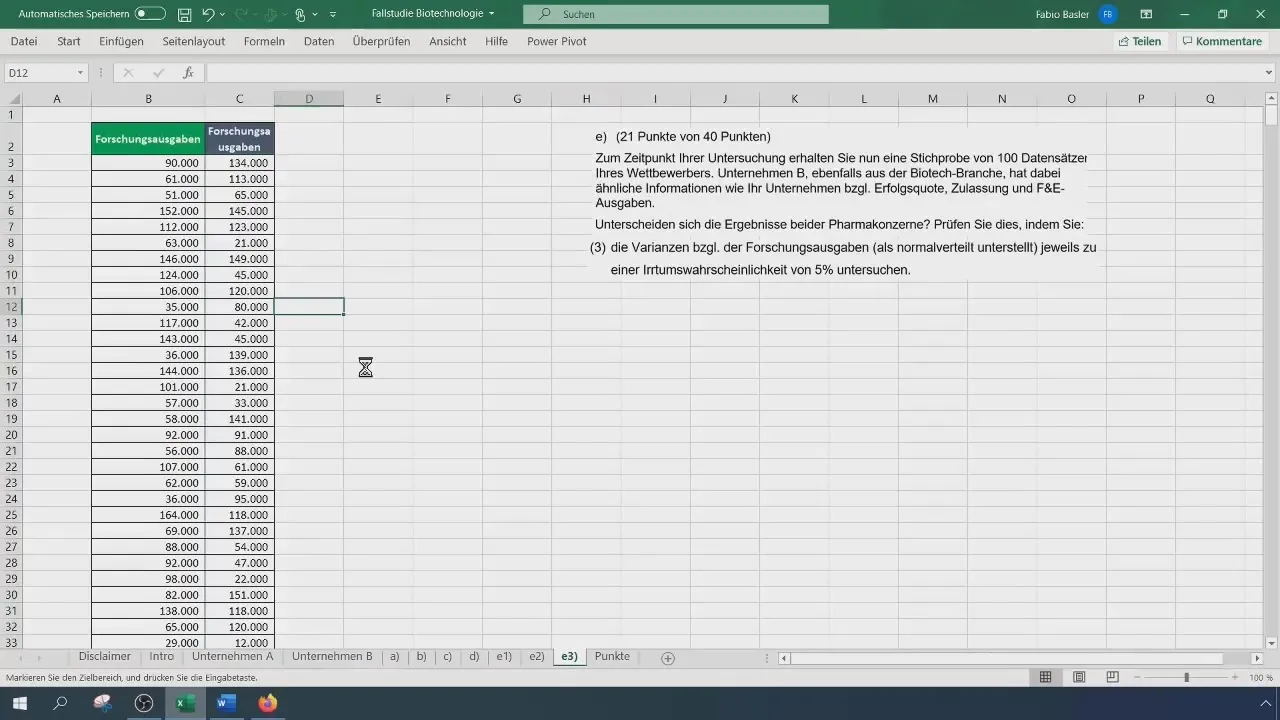
Først trenger du rådataene om forskningsutgiftene til de to selskapene. Åpne Excel-filen din og kopier de respektive forskningsdataene til de to selskapene i separate kolonner.

Trinn 2: Beregne utvalgsstørrelse og varians
Ditt utvalgsstørrelse forblir 500 for selskap A og 100 for selskap B. For å beregne dataenes varians, bruker du funksjonen VAR.S() for å estimere variansen for gruppene. Sørg for å legge inn verdiene i Excel-format for å oppnå nøyaktige resultater.
Trinn 3: Formulere hypoteser
For F-testen må hypotesene fastsettes som følger:
- Nullhypotese (H0): σ1² = σ2² (Variansene til de to selskapene er like).
- Alternativhypotese (H1): σ1² ≠ σ2² (Variansene til de to selskapene er ulike).
Trinn 4: Beregne teststatistikken
Beregn teststatistikken (F-statistikk) ved å dividere de to variansene. Bruk formelen Varians_A / Varians_B. Hvis du har lagt inn variansene i henhold til imperialistisk, vil du få en F-statistikk for sammenligning.
Trinn 5: Bestem kritisk verdi
For å finne den kritiske F-verdien, trenger du alfaverdien (vanligvis 0,05) og frihetsgradene. Frihetsgradene beregnes som følger: df1 = n1 - 1 og df2 = n2 - 1. Beregn den kritiske verdien med funksjonen F.INV().

Trinn 6: Ta beslutning
Sammenlign den beregnede F-statistikken med den kritiske F-verdien. Hvis F-statistikken er større enn den kritiske verdien, avvis nullhypotesen, ellers ikke. I dette eksempelet er kriteriet for avvisning at teststørrelsen må være mindre enn den kvantilene verdien (kritisk F).

Trinn 7: Bruk Excel dataanalyse
Excel tilbyr også muligheten til å utføre F-testen gjennom dataanalysefunksjonen. Gå til "Data" og velg "Dataanalyse". Velg "To-utvalgs-F-test" og oppgi områdene til de to variablene og velg de relevante innstillingene.
Trinn 8: Tolke resultater
Analyser resultatene fra F-testen. Hvis den beregnede F-statistikken og p-verdien i Excel-utskriften gir de samme resultatene som din manuelle beregning, kan du konkludere med at variansene til de to selskapene er like.
Oppsummering
To-utvalgs-F-testen er et essensielt verktøy i statistisk analyse som lar deg sammenligne forskjeller i varians mellom to grupper. I denne veiledningen har du lært hvordan du utfører denne testen effektivt i Excel, fra forberedelse av data til tolkning av resultatene.
Ofte stilte spørsmål
Hva er to-utvalgs-F-testen?To-utvalgs-F-testen sammenligner variansene til to grupper for å avgjøre om de er statistisk signifikant forskjellige.
Når bør jeg bruke en F-test?En F-test brukes når du vil sjekke likheten i variansene i to uavhengige grupper.
Hvordan beregner jeg F-statistikken?F-statistikken beregnes ved å dele variansen i den første gruppen med variansen i den andre gruppen.
Hva gjør jeg hvis nullhypotesen blir avvist?Hvis nullhypotesen blir avvist, kan du anta at variansene til de to gruppene er statistisk signifikant forskjellige.
Finnes det alternativer til F-testen?Ja, du kan også bruke Bartlett-testen eller Levene-testen hvis du vil teste homogeniteten i variansen.


