Chi-kvadrat-tilpasningstest for normalfordeling med Excel

Chi-kvadrat-tilpasningstesten er en enkel metode for å teste hypotesen om hvorvidt en gitt datasett følger en normalfordeling. I denne veiledningen vil du lære hvordan du kan gjennomføre Chi-kvadrat-testen i Excel for å avgjøre om inntektene fra smarttelefoner samsvarer med en normalfordeling. Vi vil gå gjennom prosessen trinn for trinn, fra opprettelse av en klassifisert frekvenstabell til beregning av teststørrelsen og sammenligning med den kritiske verdien til Chi-kvadrat.

Viktigste funn

• Chi-kvadrat-tilpasningstesten hjelper til med å teste normalfordelinger.
• Det er viktig å opprette en klassifisert frekvenstabell.
• Teststørrelsen sammenlignes med en kritisk verdi for å avvise eller akseptere nullhypotesen.

Trinn-for-trinn-veiledning

Trinn 1: Forbered dataene

For å gjennomføre Chi-kvadrat-testen, trenger du først dataene. Kopier inntektene fra smarttelefonene til et Excel-regneark. Sørg for at dataene dine er organisert i én kolonne.

Trinn 2: Opprett histogram

For å få de første visuelle tegnene på fordelingen, opprett et histogram av dataene dine. Gå til "Sett inn" og velg "Diagrammer". Legg til et histogram ved å velge området for dataene.

Trinn 3: Opprett klassifisert frekvenstabell

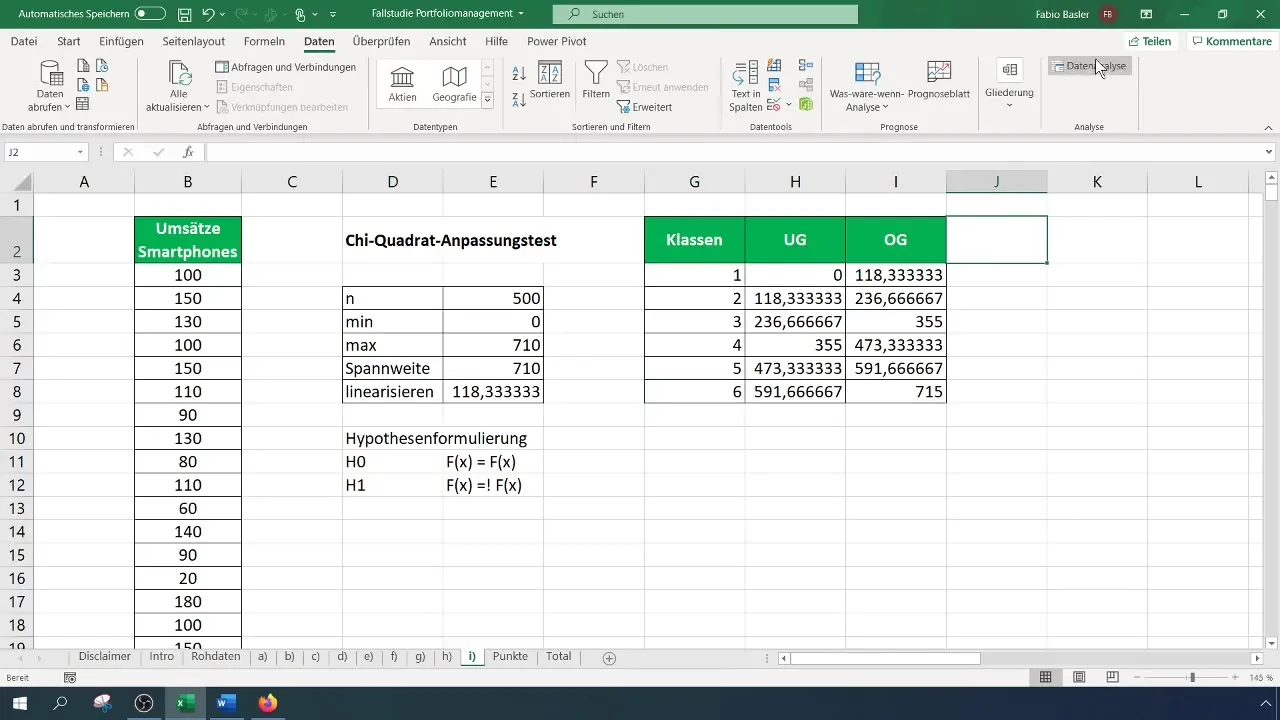
For Chi-kvadrat-testen trenger du en klassifisert frekvenstabell. Bestem antall klasser for tabellen din på forhånd – i dette tilfellet bruker vi seks klasser. Beregn intervallbredden og opprett tabellen deretter.

Trinn 4: Beregne frekvenser

Nå må du beregne de observerte frekvensene for hver klasse. Gå til "Dataanalyse" i menyen og velg "Histogram". Velg inndataområdet for dataene dine og klassenes grenser. Bestem utdataområdet for frekvenstabellen.

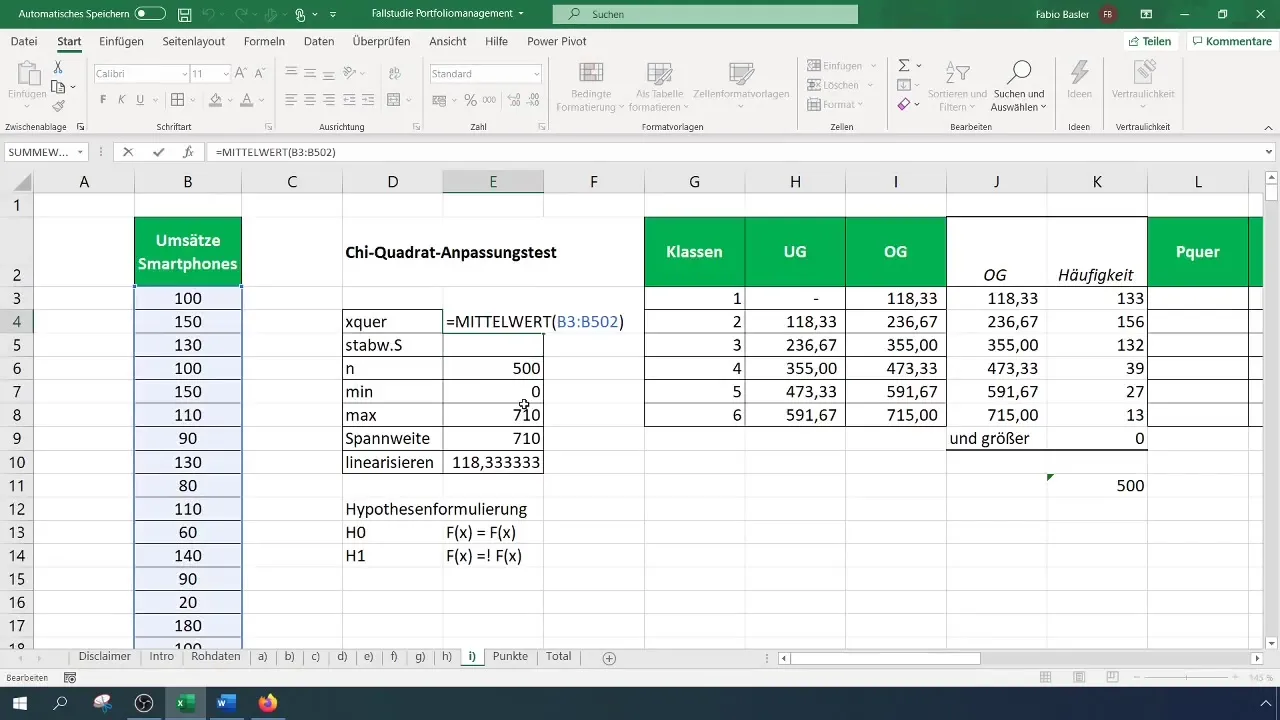
Trinn 5: Beregne forventede frekvenser

For å finne de forventede frekvensene, beregn sannsynlighetene for hver klasse basert på den antatte normalfordelingen. Du trenger gjennomsnittet og standardavviket for dataene dine for dette formålet.

Trinn 6: Beregne teststørrelse

Beregn teststørrelsen (Chi-kvadrat) med formelen:

[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]

der (O_i) er de observerte og (E_i) er de forventede frekvensene. Du kan gjøre denne beregningen i Excel ved å lagre de ulike komponentene i separate celler.

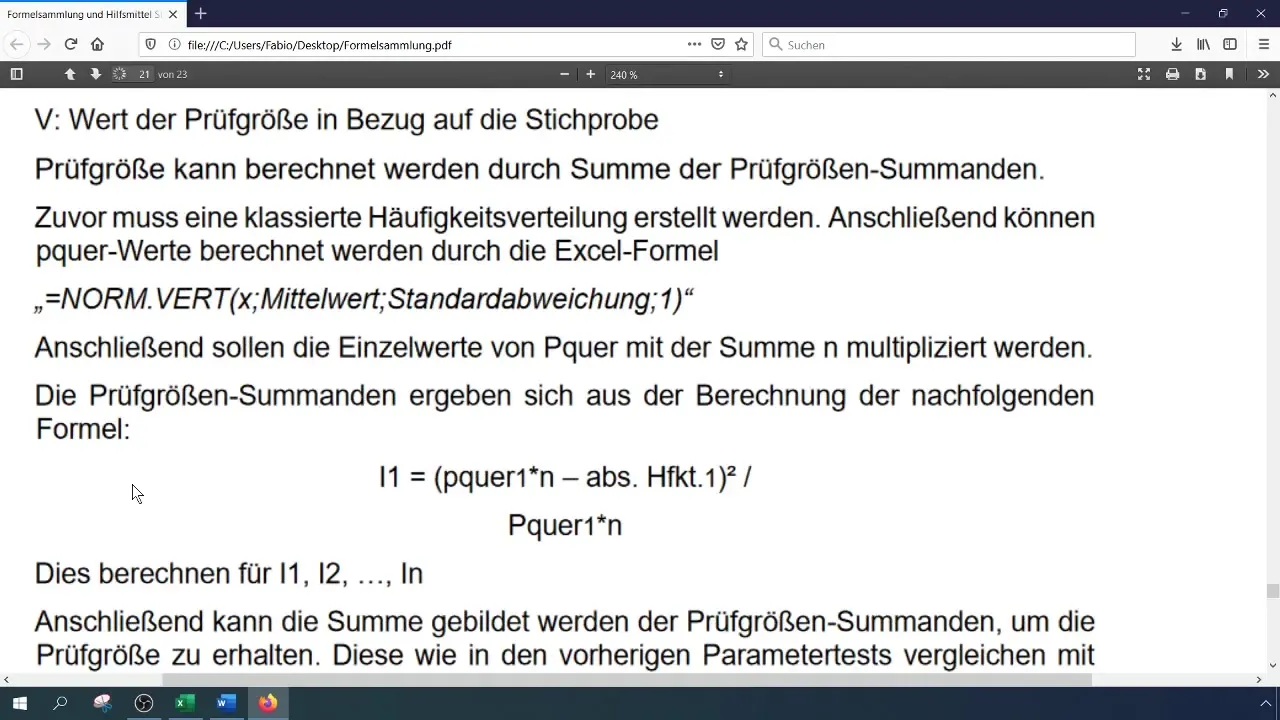
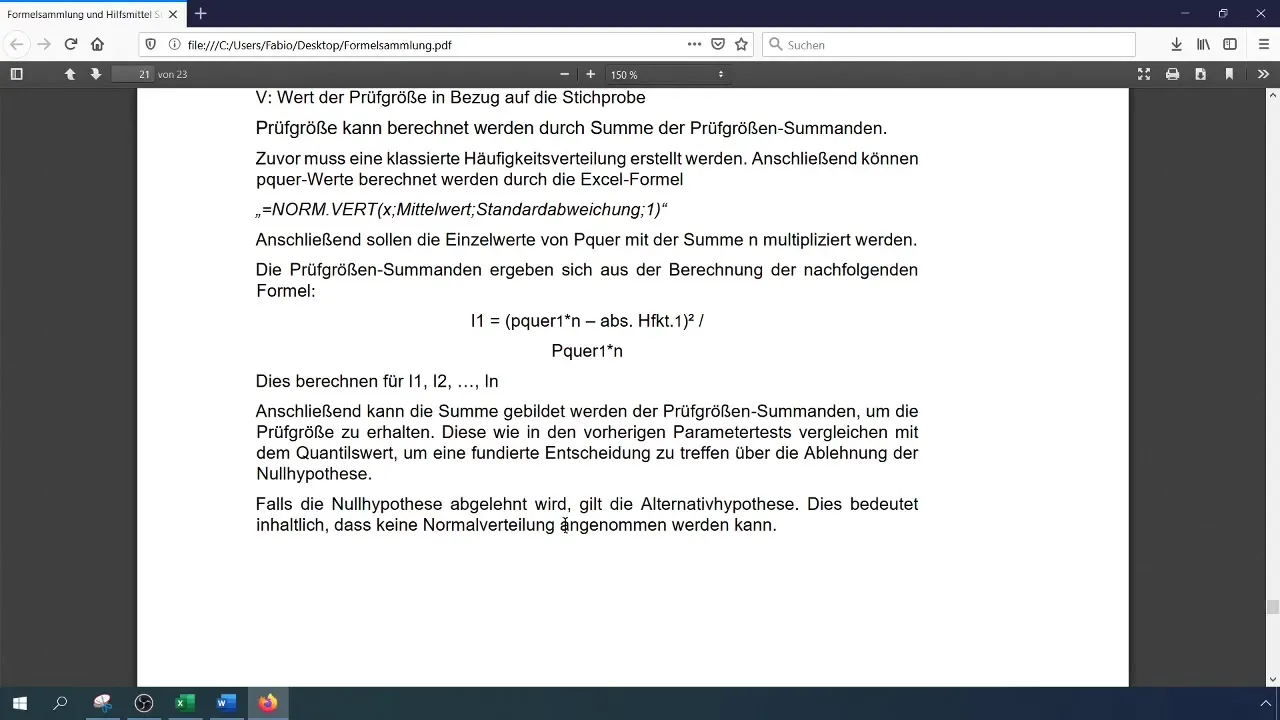
Trinn 7: Beregne kritisk verdi

For å vurdere teststørrelsen, må du beregne den kritiske verdien ( \chi^2 ) for ditt konfidensnivå og antall frihetsgrader. Antallet frihetsgrader for Chi-kvadrat-testen er (k - 1), der (k) er antallet klasser.

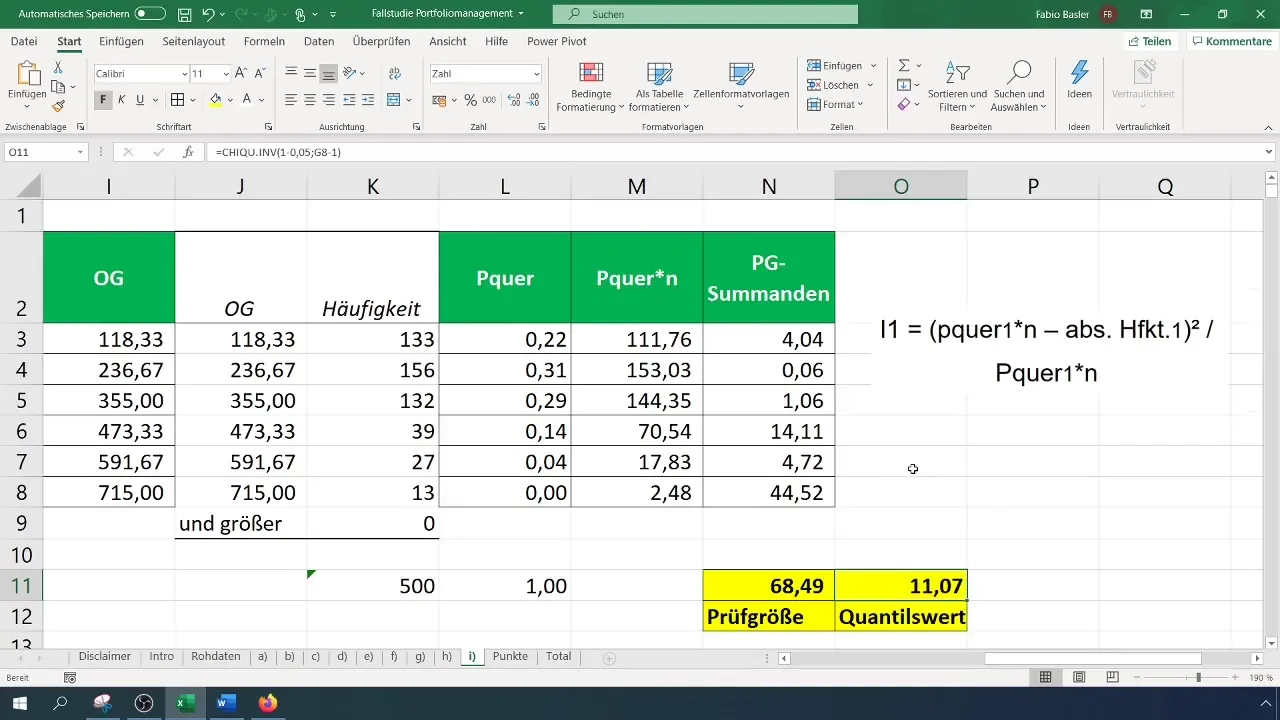
Trinn 8: Teste hypotesene

Sammenlign den beregnede teststørrelsen med den kritiske verdien. Hvis teststørrelsen er større enn den kritiske verdien, avvis nullhypotesen, noe som betyr at dataene ikke er normalfordelt. Ellers aksepteres nullhypotesen.

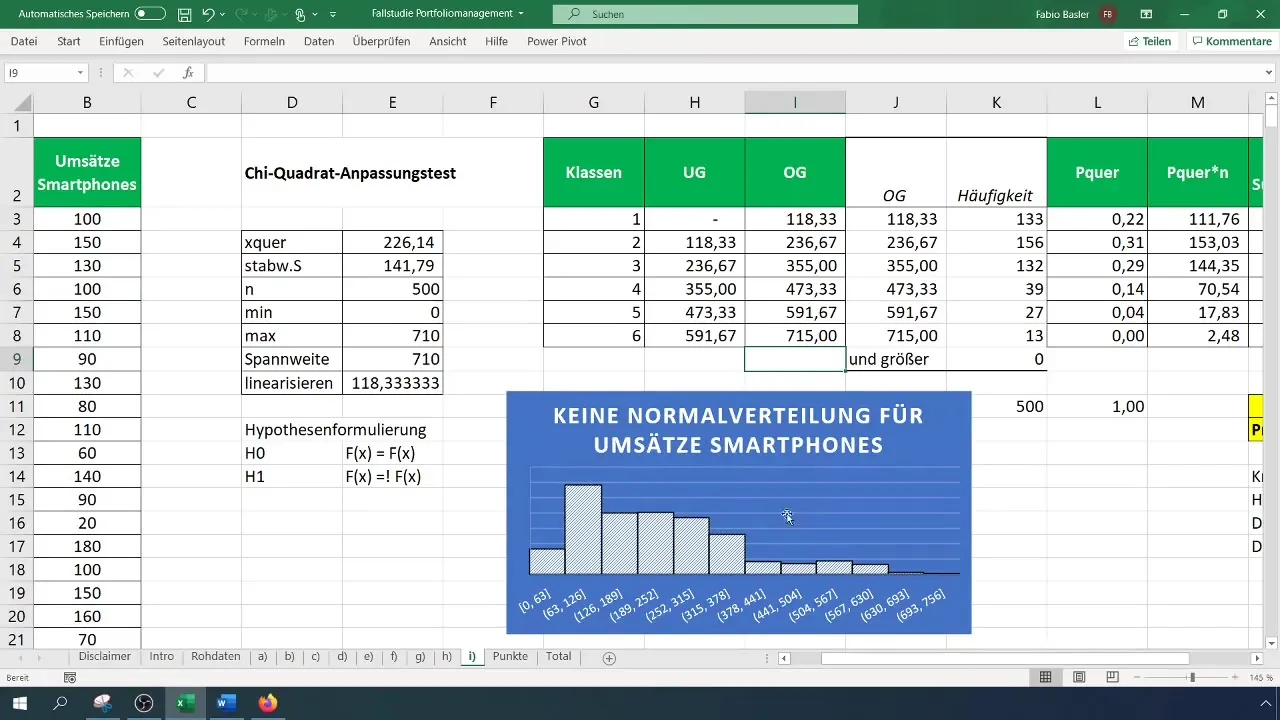
Trinn 9: Oppsummer resultater

Hold resultatene dine fast, og utvid dem med grafiske data og hypotesetestene. Ikke glem å sjekke histogrammet ditt for å visuelt bekrefte at fordelingen ikke er normal.

Oppsummering

I løpet av denne veiledningen har du lært hvordan du utfører Chi-kvadrat-tilpasningstesten i Excel for å analysere normalfordelingen av smarttelefonomsetningene dine. Trinnene inkluderer å lage en klassifisert frekvenstabell, beregninger for forventede frekvenser, teststatistikken og til slutt sammenligne den med den kritiske verdien.