Gjennomføring av en tostikkprøve F-test i Excel

Statistiske hypotesetester er et uunnværlig verktøy for bedrifter å ta funderte beslutninger. I følgende avsnitt viser vi deg hvordan du utfører en to-utvalgs-F-test i Excel for å sjekke gyldigheten av hypotesene dine om variasjonen i salgsdataene dine. Denne veiledningen vil følge deg steg for steg gjennom prosessen, slik at du kan bruke de lærte teknikkene trygt.

Viktigste funn

• To-utvalgs-F-test brukes til å sammenligne variasjonene i to grupper med data.
• Målet er å sjekke om variasjonen i nåværende salgsdata avviker fra en antatt verdi.
• Excel tilbyr verktøyene for å utføre nødvendige beregninger og sammenligninger.

Trinn-for-trinn veiledning

1. Forberedelse av data

Før du starter testen, sørg for at dataene dine er klargjort. Det er viktig å fjerne filtrene for å ta hensyn til all relevant data. Begynn med å velge dataene i de relevante kolonnene.

2. Fastsettelse av parametere

Definer parameterne for testen din. Du bør vite hvor mange datapunkter du analyserer. I vårt eksempel antar vi at du har 100 salgstall som følger en normalfordeling.

3. Registrering av tidligere variansverdi

Den kjente varians- eller omsetningsverdien fra fortiden spiller en sentral rolle i analysen din. I dette eksemplet er den tidligere verdien 116 millioner euro per uke.

4. Formulering av hypoteser

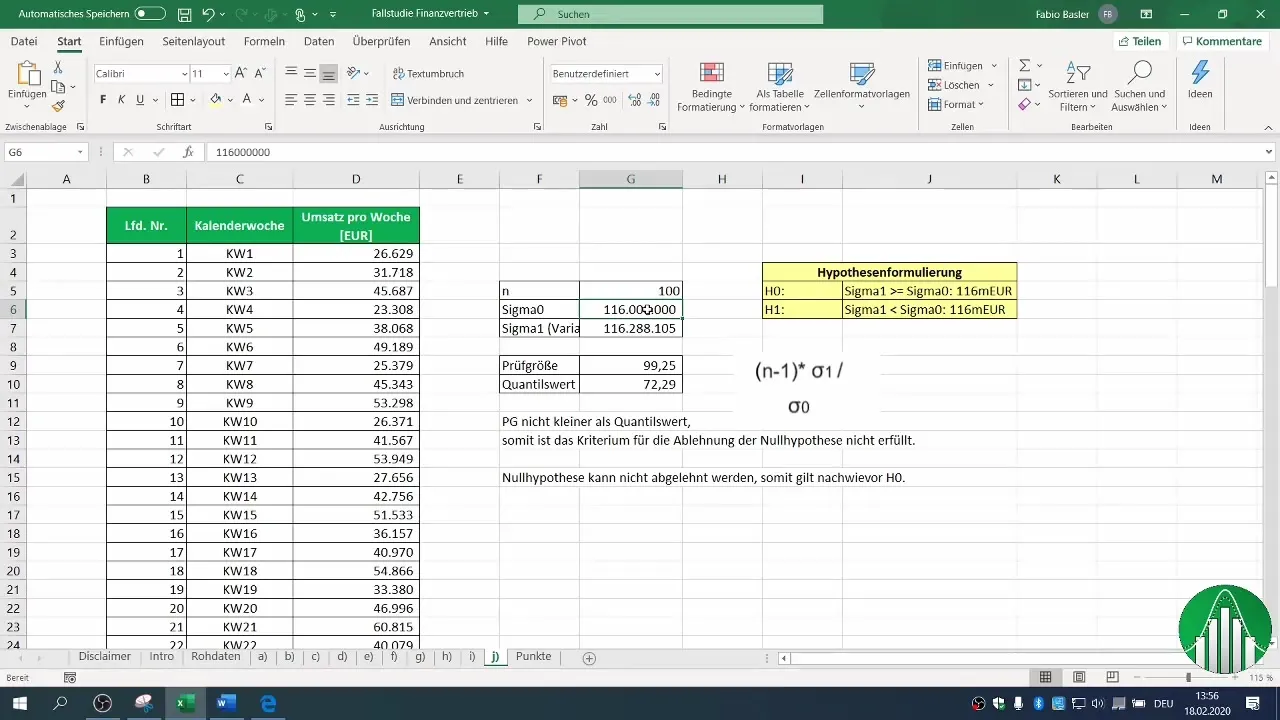
Formuler nullhypotesen din (H0) og alternativhypotesen (H1). I dette tilfellet sier H0 at variansen forblir lik eller større enn 116 millioner, mens H1 antyder at variansen har blitt redusert.

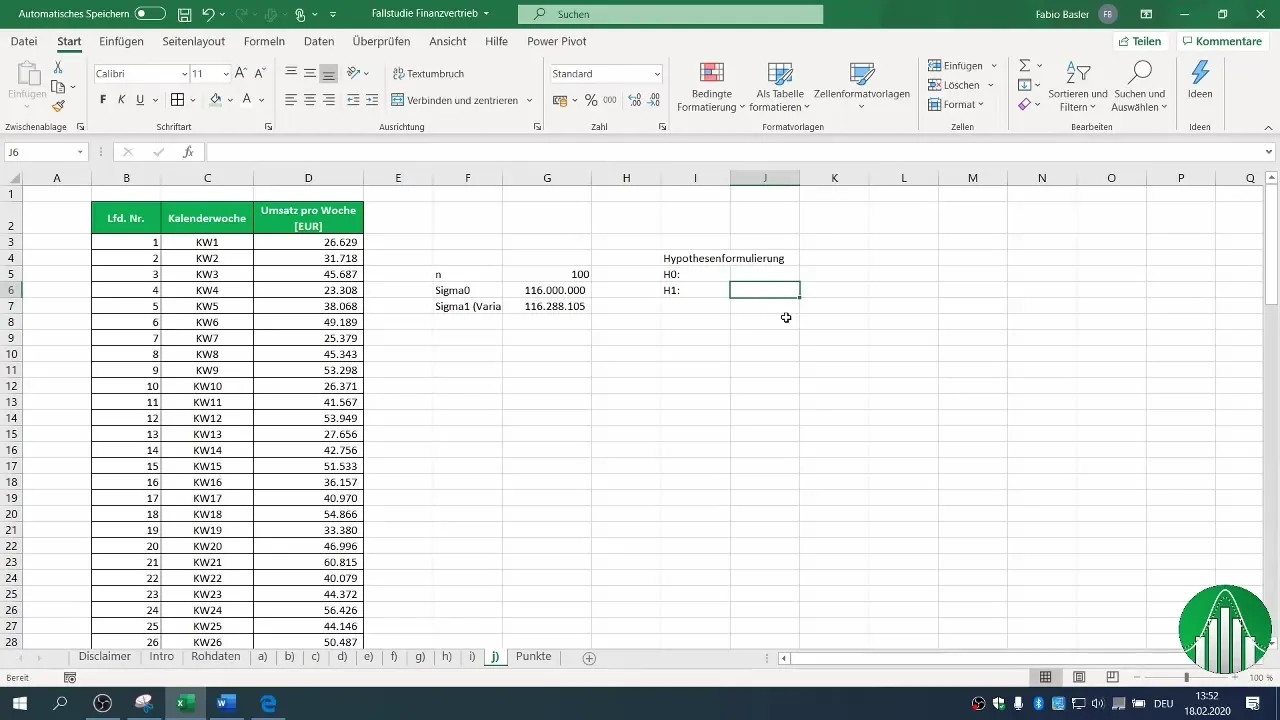
5. Beregning av teststørrelse

Du kan beregne teststørrelsen ved hjelp av variansen til utvalget ditt. Gjennomfør nødvendige beregninger for å finne verdien for teststørrelsen din. Denne beregnes ved hjelp av formelen: (n-1) * σ1 / σ0, der σ1 er variansen i utvalget ditt og σ0 representerer variansen fra fortiden.

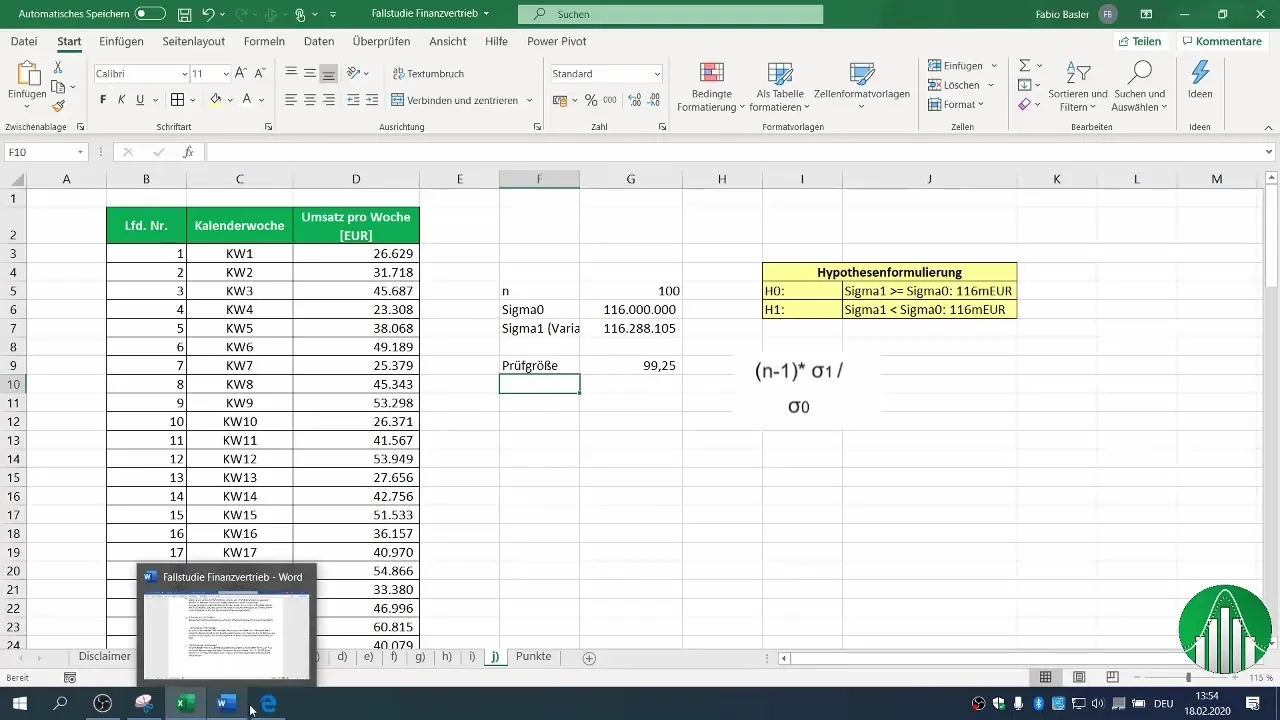
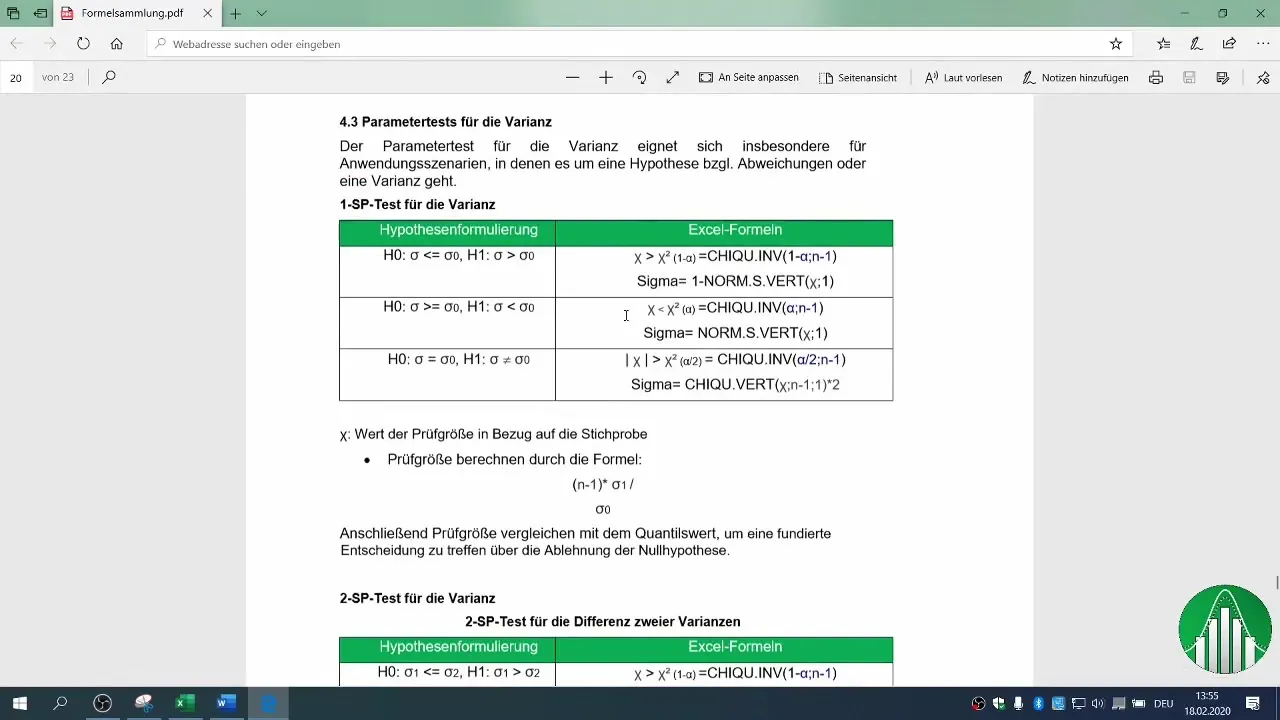
6. Bestemmelse av kritisk område

For å avgjøre om du kan forkaste nullhypotesen, må du definere det kritiske området. Bruk chi-kvadrat-fordelingstabellen for ditt konfidensnivå. I vårt eksempel brukte vi en feilmargin på 2%.

7. Sammenligning av teststørrelse og kritisk størrelse

Sjekk nå om teststørrelsen din er mindre enn den kritiske verdien. I dette tilfellet fant vi ut at teststørrelsen vår ikke er mindre enn den kritiske kvantilverdien.

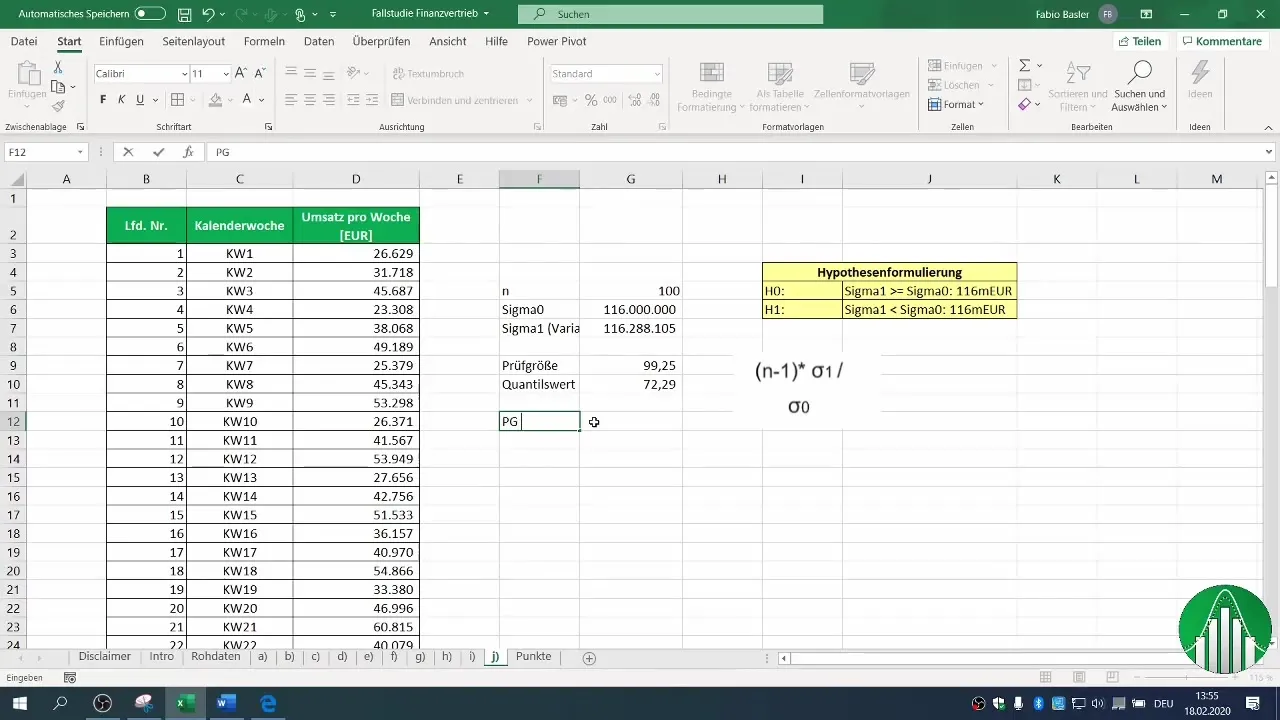
8. Trekke konklusjoner

Basert på sammenligningen din kan du nå bestemme om du kan forkaste nullhypotesen eller ikke. I vårt eksempel fant vi ut at nullhypotesen ikke kan forkastes. Dette antyder at variansen i salgsdataene dine fremdeles samsvarer med eller til og med er større enn den antatte verdien.

Oppsummering

I denne veiledningen har vi grundig dekket hvordan du utfører en to-utvalgs-F-test i Excel. Du har lært hvordan du klargjør dataene dine, formulerer hypoteser, beregner teststørrelsen, bestemmer det kritiske området og til slutt trekker konklusjoner. Med disse trinnene er du godt rustet til å utføre statistiske analyser på egenhånd.