Beregning av Spearman rangkorrelasjon i Excel

Rangkorrelasjonsanalysen er av sentral betydning i den statistiske undersøkelsen av relasjoner mellom variable. Spesielt når det gjelder ordinalskalerte data, er Spearman-rangkorrelasjonen en verdifull metode for å oppdage mønstre og forbindelser. I denne veiledningen vil du steg for steg lære hvordan du kan beregne rangkorrelasjonen etter Spearman for en undersøkelse ved hjelp av Excel.

Viktigste funn

• Rangkorrelasjon måler styrken og retningen av et monotonisk forhold mellom to ordinale variable.
• Spearman-rangkorrelasjonskoeffisienten er spesielt egnet når en av variablene er ordinal og den andre er metrisk skalert.
• Beregningen i Excel kan utføres ved hjelp av enkle formler og funksjoner.

Trinnvis veiledning

Først definerer vi variablene vi ønsker å analysere. I dette tilfellet er det kundetilfredshet (ordinalskalert, verdier 1-3) og antall bestillinger (metrisk skalert).

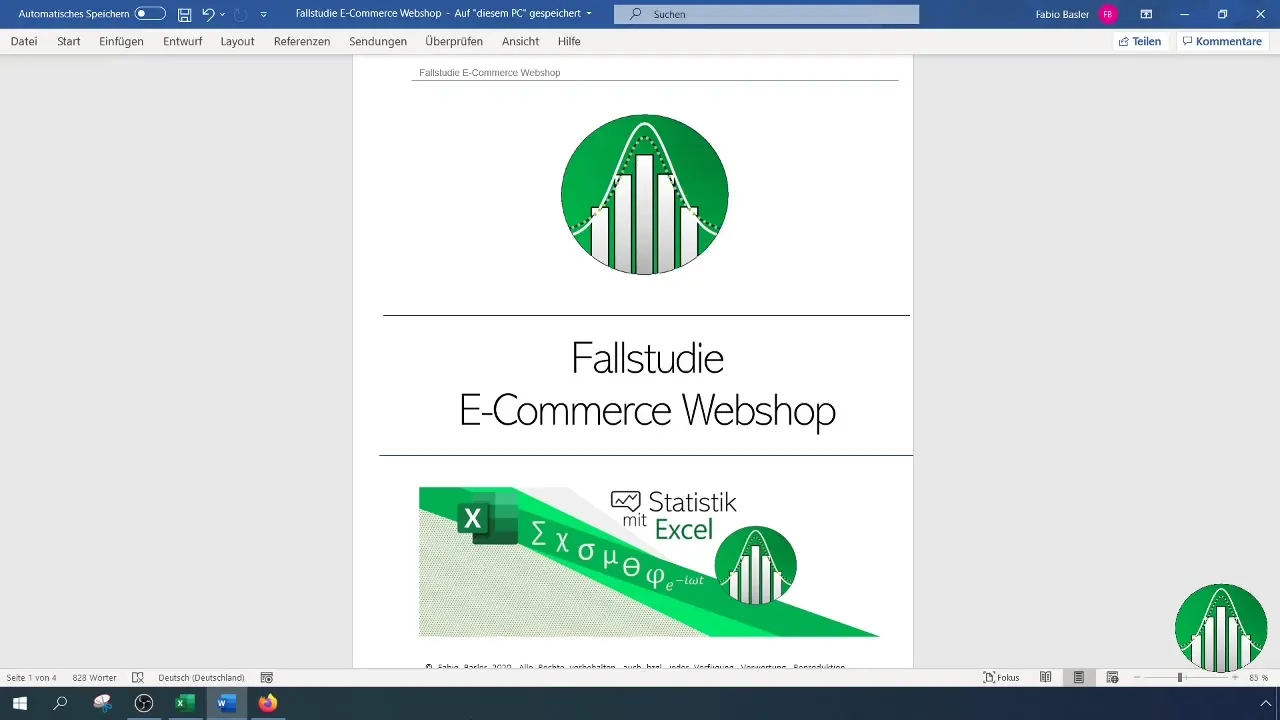
For å lage en rangordning for kundetilfredshet og antall bestillinger trenger du en tabell som inneholder de relevante dataene. Sørg for å skrive inn disse dataene i Excel.

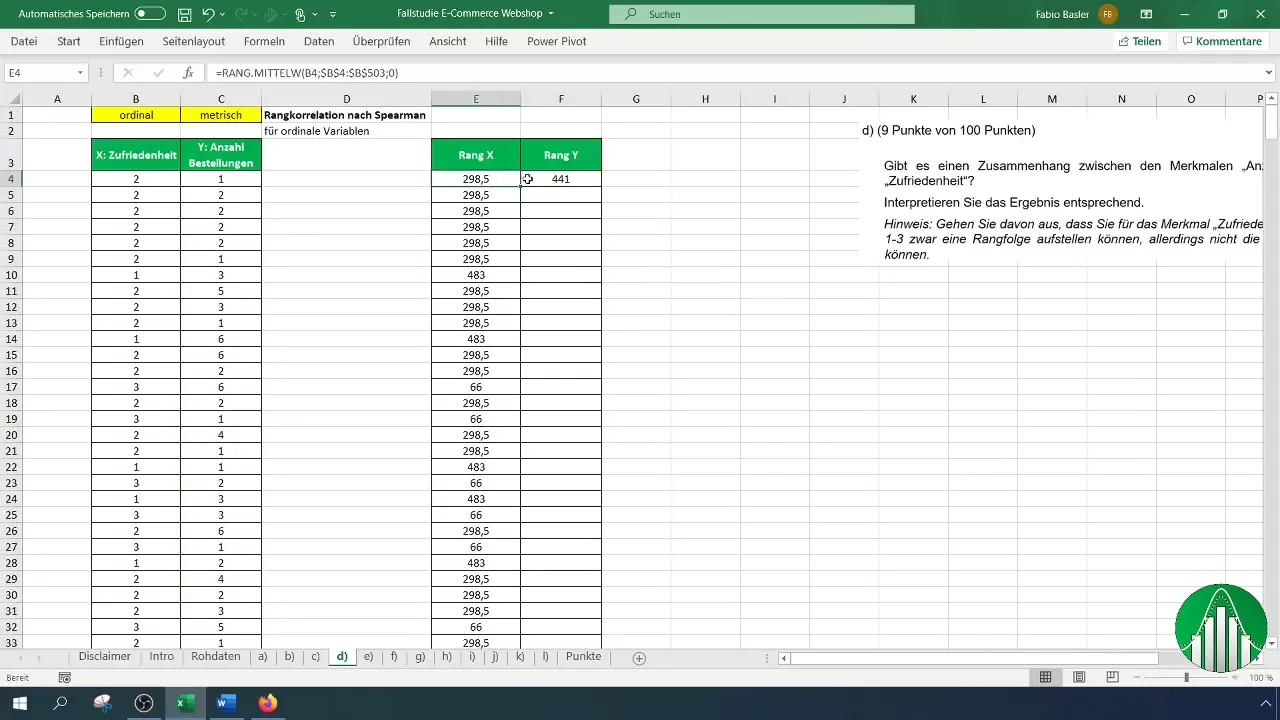
Etter at du har skrevet inn dataene i Excel, skal vi se på beregningen av rangkorrelasjon etter Spearman. For dette bruker vi funksjonen "Rang.Mid" i Excel, som returnerer rangen til et tall innen en liste. For kundetilfredshet bruker vi først formelen:

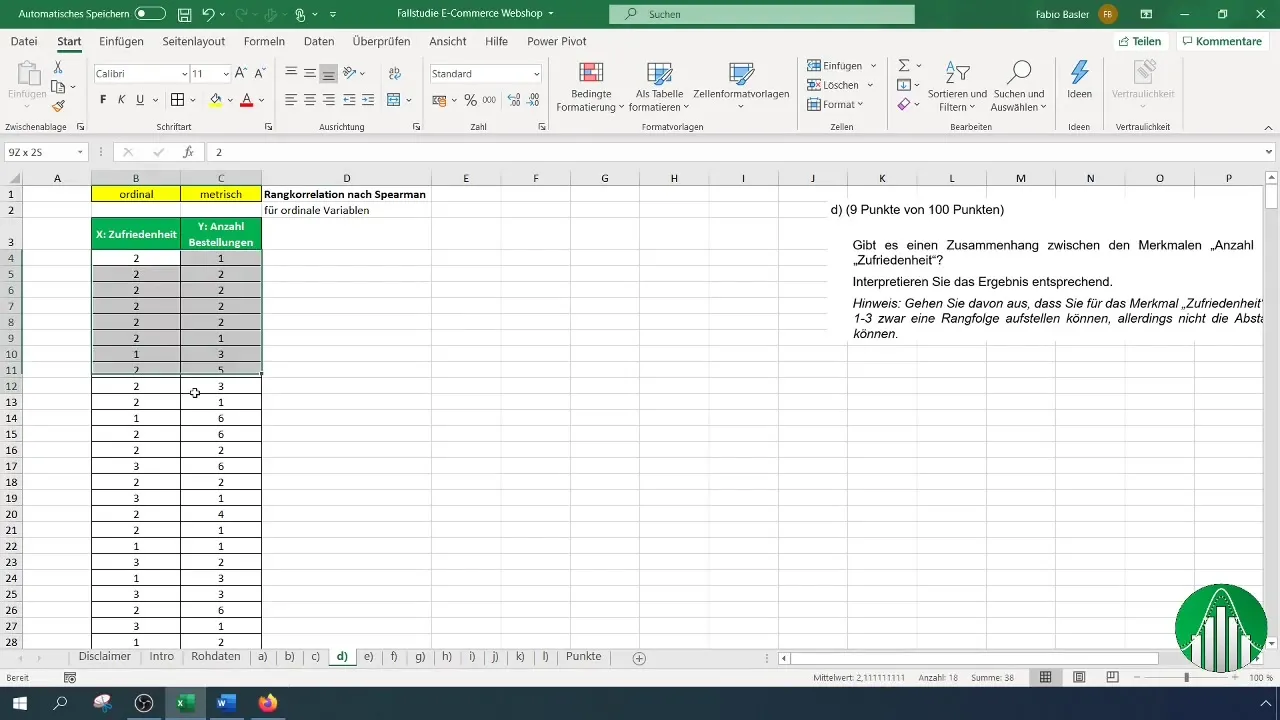
Ved bruk av denne formelen må du merke kolonnen for kundetilfredshet og angi hele området fra B4 til slutten av dataserien din for å identifisere rangene riktig.

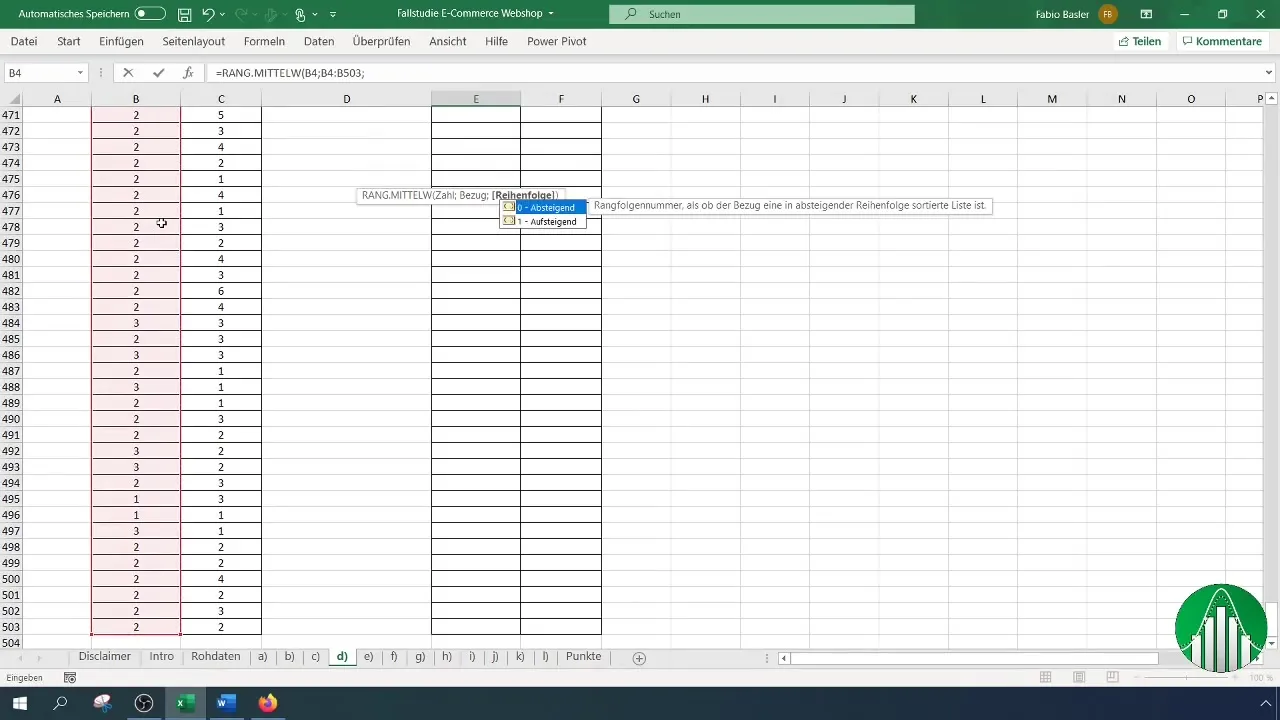
Bestem om du ønsker å sortere rangene stigende eller synkende. Det er vanligvis hensiktsmessig å sortere dem stigende. Legg merke til at cellehenvisningene for rangene må være faste ved å bruke F4-tasten. Dette er viktig for at henvisningene ikke endres under kopieringsprosessen.

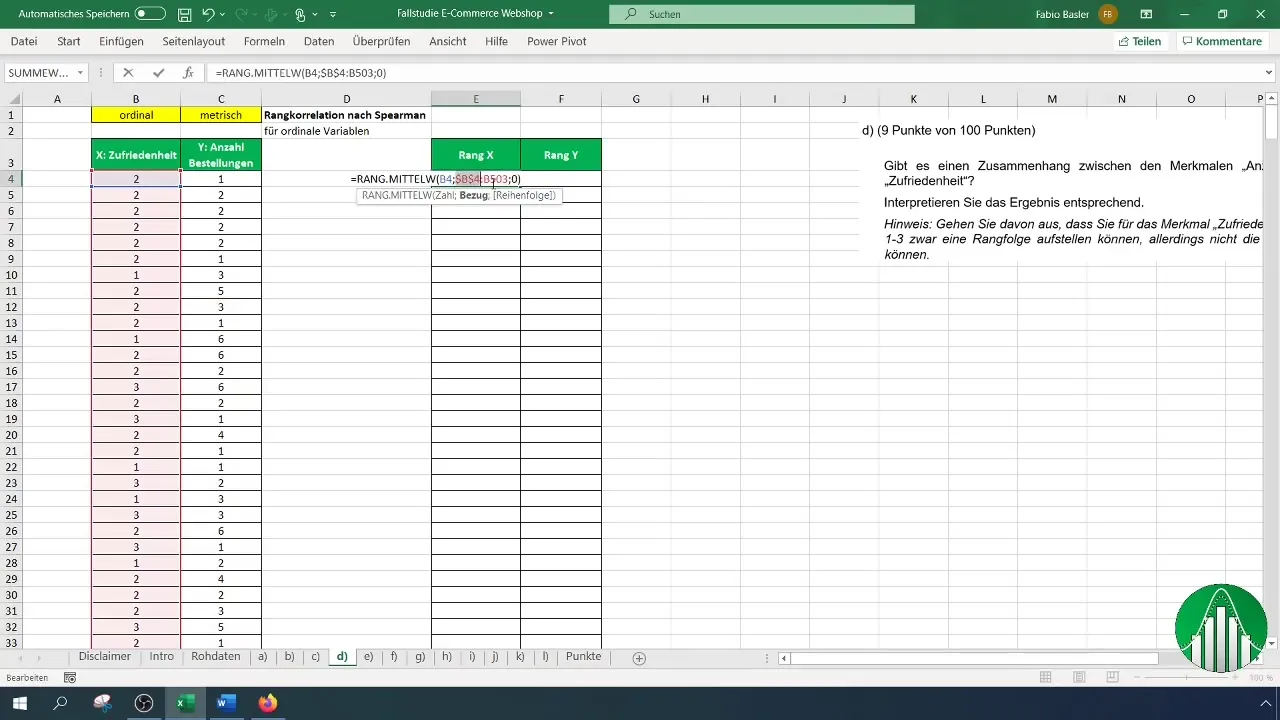
Når du har bestemt rangene for kundetilfredshet, gjentar du prosessen for antall bestillinger. Forsikre deg om at du bruker formelen og henvisningen riktig.

Med begge ranglistene (kundetilfredshet og antall bestillinger) er du klar til å beregne rangkorrelasjonskoeffisienten etter Spearman. Du bruker formelen "=KORREL" for å bestemme forholdet. Syntaksen ser slik ut:

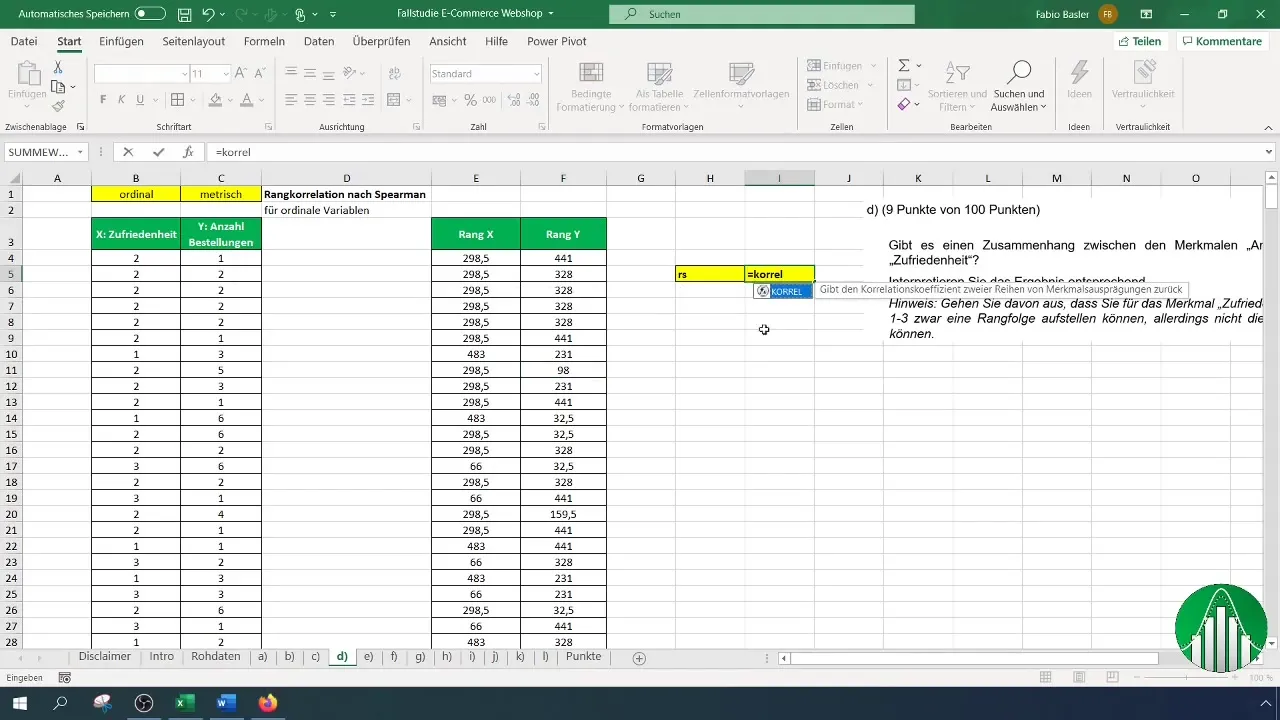
Angi ranglisten for kundetilfredshet for første referanse og ranglisten for bestillinger for andre referanse. Excel vil nå automatisk beregne Spearman's rangkorrelasjonskoeffisient.

Hva ble resultatet av beregningen din? En verdi på 5,61% indikerer en svak positiv sammenheng mellom kundetilfredshet og antall bestillinger. Dette betyr at det er knapt noen signifikant relasjon mellom disse to variablene.

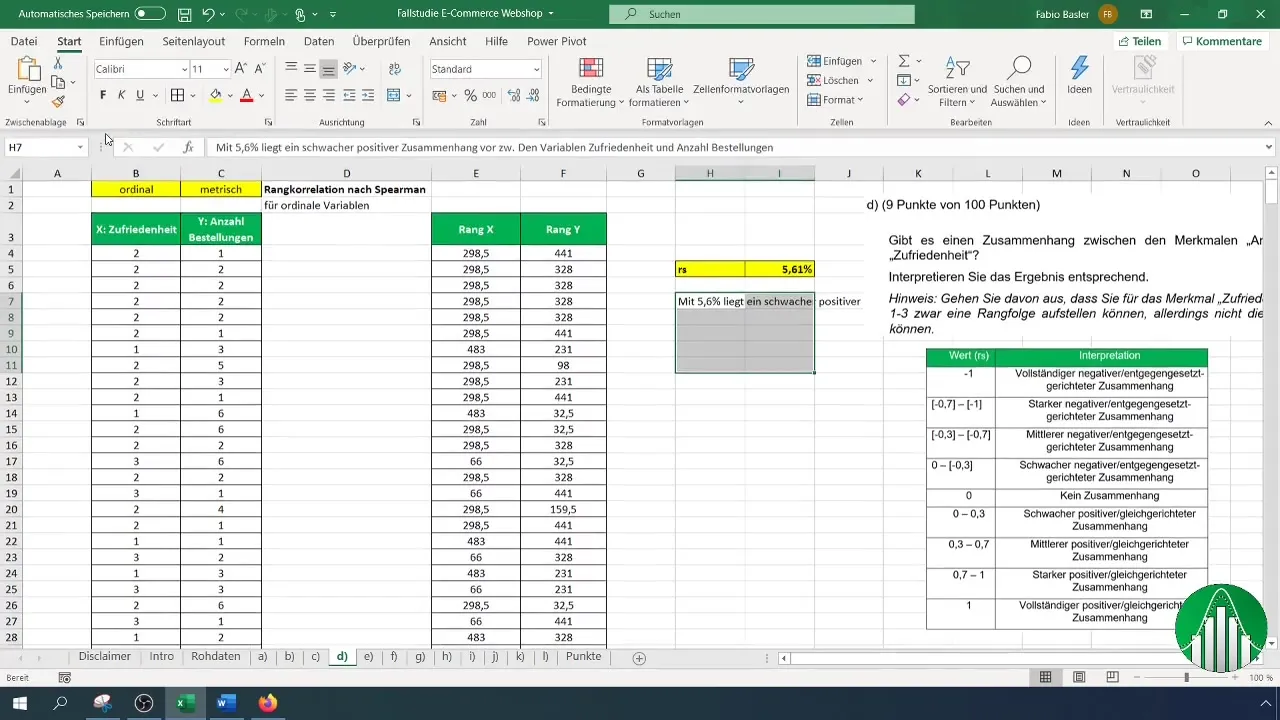
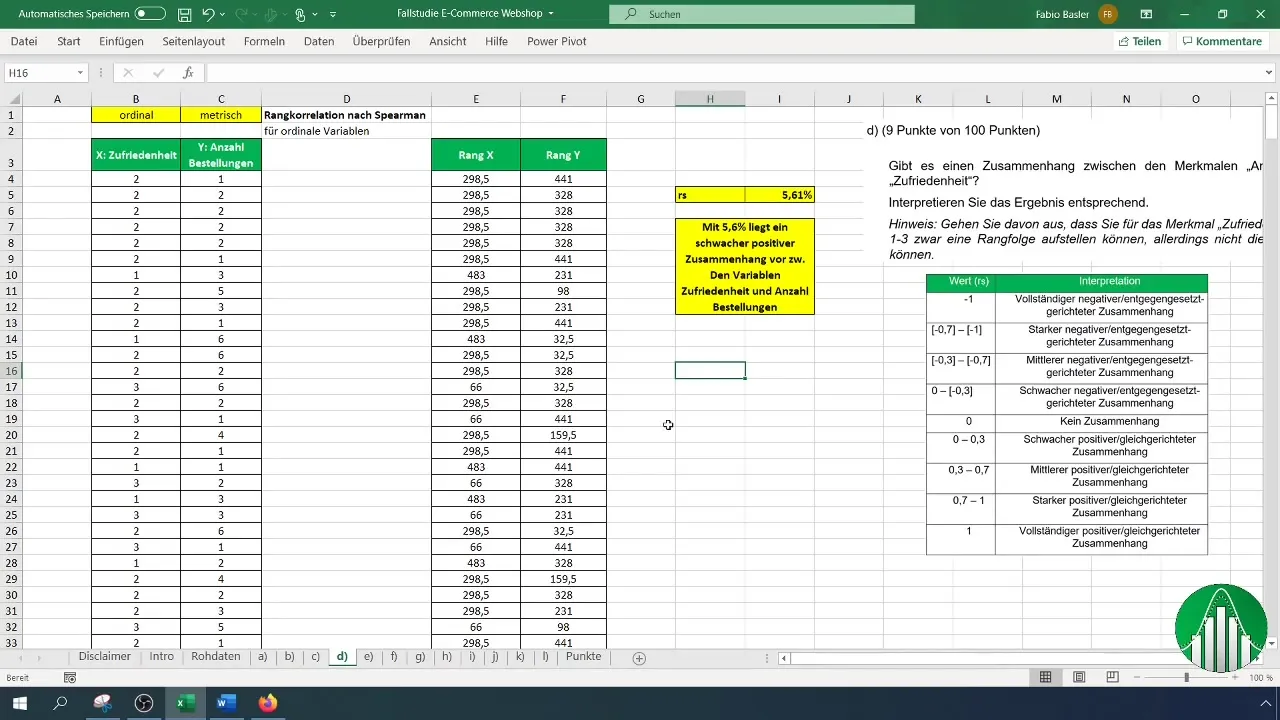
For å tolke resultatene dine, bruk en verditabell som viser de ulike områdene av rangkorrelasjon. Etter tolkningen bekrefter vi at den lave korrelasjonsgraden betyr at variablene er relativt uavhengige.

Oppsummering

Gjennomføringen av en rangkorrelasjonsanalyse etter Spearman i Excel gir deg verdifulle innsikter i relasjonene mellom ordinale og metriske variable. Metoden er enkel å bruke og gir en klar oversikt over eventuelle forbindelser.