Statistiske beregninger er en uunnværlig del av dataanalysen, spesielt i en E-handelskontekst. Den historiske dataanalysen gjør det mulig å beregne sannsynligheter som er avgjørende for bedrifter. I denne veiledningen vil du lære hvordan du kan beregne sannsynligheter ved hjelp av Poisson-distribusjonen i Excel, basert på et case med en spørreundersøkelse.
Viktigste funn Poisson-distribusjonen gjør det mulig å bestemme sannsynligheten for hendelser som skjer innenfor et fast tidsintervall. I dette eksempelet skal du beregne sannsynligheten for at mer enn to, men maksimalt fire kunder kjøper noe i en E-handelsbutikk innenfor en time, samt sannsynligheten for at mer enn to kunder totalt kjøper noe.
Trinnvis veiledning
La oss starte med å beregne sannsynlighetene for de beskrevne hendelsene.
Trinn 1: Forstå grunnleggende om Poisson-distribusjonen
Først og fremst er det viktig at du forstår hva Poisson-distribusjonen er. Denne diskrete sannsynlighetsdistribusjonen brukes til å kvantifisere antall hendelser i faste tidsperioder. I dette eksempelet har vi en gjennomsnittlig på fem kjøp per time. Dette formulerer du som en lambda-verdi (λ = 5).

Trinn 2: Forberede data i Excel
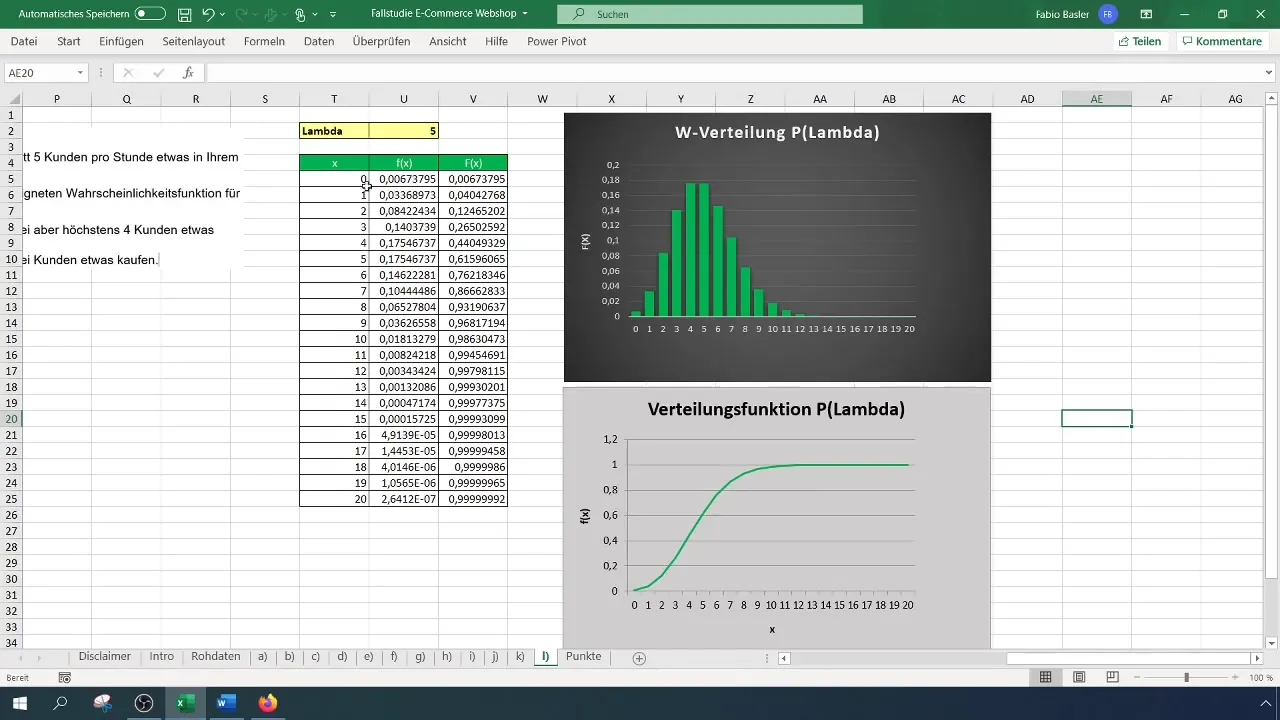
Åpne Excel og forbered en ny tabell. Forsikre deg om at du har de relevante parametrene (Lambda og antallet ønskede hendelser) tydelig synlig.
Trinn 3: Beregne sannsynligheter for kundekjøp
For det første scenariet ønsker du å beregne sannsynligheten for at mer enn to og maksimalt fire kunder kjøper noe. For å gjøre dette må du beregne sannsynlighetene for to og fire kunder, og deretter finne differansen mellom dem.

Trinn 4: Bruke Excel-formelen for Poisson-distribusjonen
Bruk funksjonen POISSON.WAHRSCHEINLICHKEIT for å beregne sannsynlighetene. Formelen er som følger:
- For to kjøpere: =POISSON.WAHRSCHEINLICHKEIT(2; 5; WAHR).
- For fire kjøpere: =POISSON.WAHRSCHEINLICHKEIT(4; 5; WAHR).
Trinn 5: Tolke resultatene
Etter å ha anvendt formelene, vil du få to sannsynligheter, for eksempel 12% for to kunder og 44% for fire kunder. Deretter trekker du sannsynligheten for to kunder fra sannsynligheten for fire kunder, noe som gir deg en sannsynlighet på 32% for at mer enn to men maksimalt fire kunder kjøper noe.
Trinn 6: Beregne ytterligere sannsynligheter
Nå er det på tide å beregne sannsynligheten for at mer enn to kunder kjøper noe i din E-handelsbutikk. For dette beregner du først sannsynligheten for nøyaktig to kjøpere og trekker dette resultatet fra 1.
Trinn 7: Bruke Excel-formelen for mer enn to kjøpere
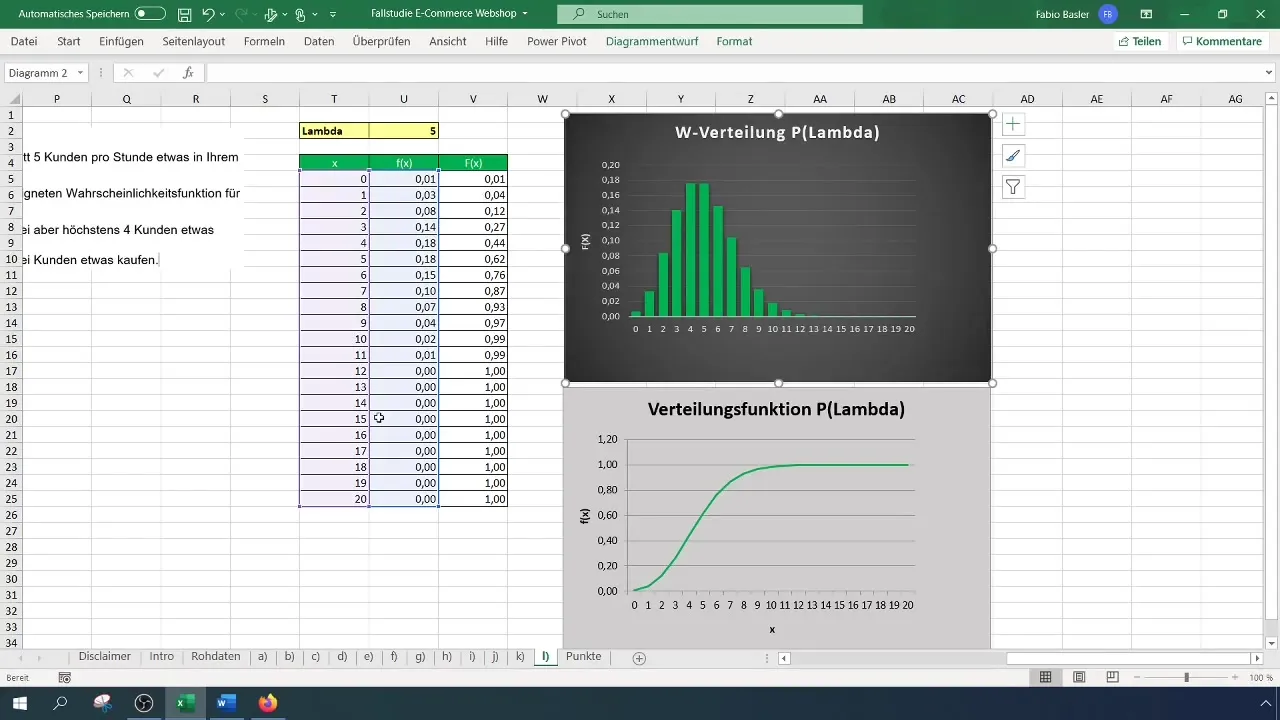
Excel-formelen er: =1 - POISSON.WAHRSCHEINLICHKEIT(2; 5; WAHR). Dette gir deg sannsynligheten for at mer enn to kunder kjøper noe, som i dette tilfellet er 88%.
Trinn 8: Oppsummere resultatene
Etter å ha gjennomført alle beregningene, skriver du ned de viktigste sannsynlighetene. Du har funnet ut at sannsynligheten for at mer enn to, men maksimalt fire kunder bestiller, er 32%, mens sannsynligheten for at mer enn to kunder totalt kjøper noe, er 88%.
Oppsummering
I denne veiledningen har du lært hvordan du kan bruke Poisson-distribusjonen til å beregne sannsynligheter i Excel. Du har fulgt trinn for å beregne og tolke sannsynligheter for spesifikke hendelser.
Ofte stilte spørsmål
Hva er Poisson-distribusjonen?Poisson-distribusjonen er en diskret sannsynlighetsdistribusjon som angir hvor mange ganger en hendelse skjer i en fast tidsperiode.
Hvordan beregner jeg sannsynligheter med Poisson-distribusjonen i Excel?Du bruker funksjonen POISSON.WAHRSCHEINLICHKEIT for å beregne sannsynligheter for ulike verdier.
Hva betyr en Lambda-verdi på 5?En Lambda-verdi på 5 betyr at gjennomsnittlig fem hendelser (f.eks. kjøp) skjer i den definerte tidsperioden (f.eks. en time).
Hvilke verdier må jeg oppgi for Poisson-distribusjonen?Du må oppgi antall ønskede hendelser (x), gjennomsnittet (λ) og om du ønsker å beregne kumulative sannsynligheter.
Hvorfor er Poisson-distribusjonen viktig for E-handel?Poisson-distribusjonen hjelper til med å analysere kjøpsmønstre og forutsi sannsynligheten for kundeaktiviteter, noe som kan støtte viktige beslutninger innen markedsføring og lagerstyring.


