Test dwóch prób niezależnych to narzędzie krytyczne w statystyce do badania różnic między dwoma średnimi. W tym samouczku dowiesz się, jak przeprowadzić ten test w Excelu w sposób prosty i skuteczny. Na przykładzie z dziedziny biotechnologii nauczysz się porównywać i analizować statystycznie wskaźniki sukcesu dwóch konkurencyjnych firm.
Najważniejsze wnioski
- Zastosowanie testu dwóch prób niezależnych do analizy różnicy między dwiema średnimi.
- Formułowanie i sprawdzanie hipotez.
- Wykorzystanie programu Excel do obliczeń i prezentacji wyników.
Krok po kroku
Najpierw rozpocznijmy od stworzenia niezbędnych danych oraz przeprowadzenia testu w Excelu.
Krok 1: Przygotowanie danych
Rozpocznij od zebrania danych surowych dotyczących wskaźników sukcesu obu firm. Zakładamy, że masz dostępne dane dla firm A i B. Posiadasz przykładową próbę 100 rekordów dla każdej z firm.

Krok 2: Obliczanie liczby próbek i średnich
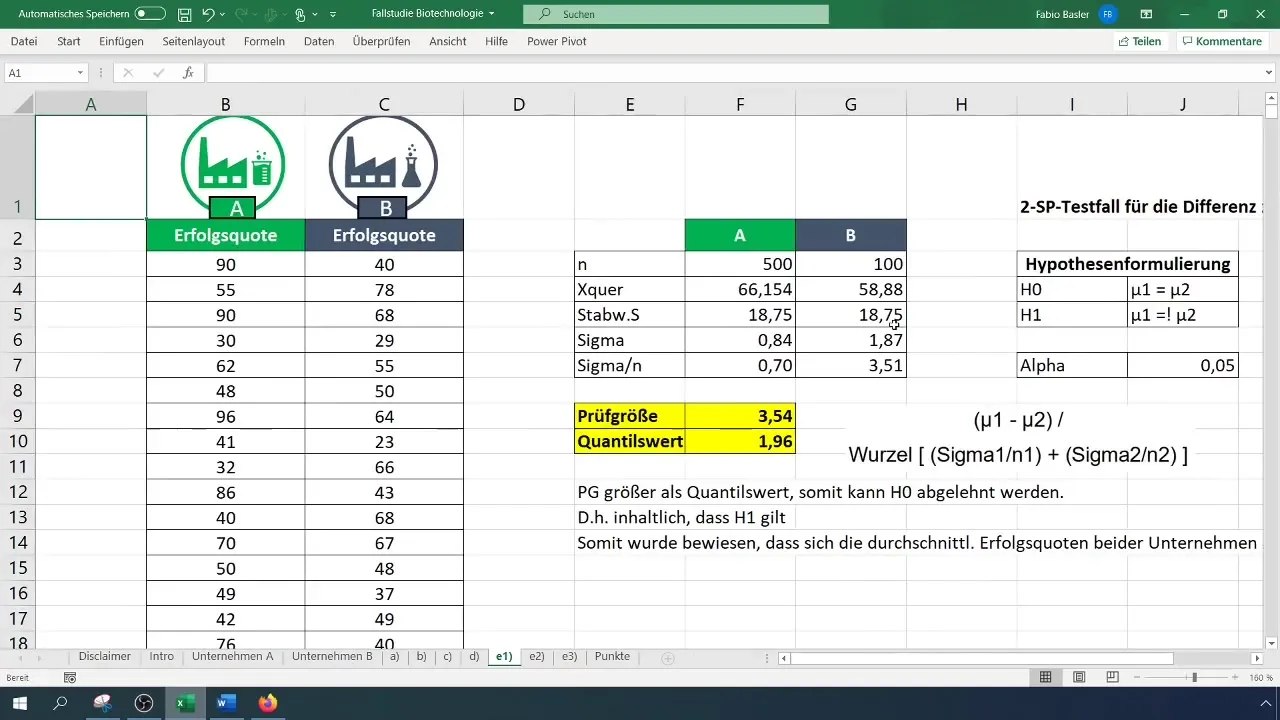
Stwórz tabelę w Excelu, aby zestawić próbki i ich średnie. Oblicz najpierw liczbę próbek (N) dla obu firm oraz średnią (X).

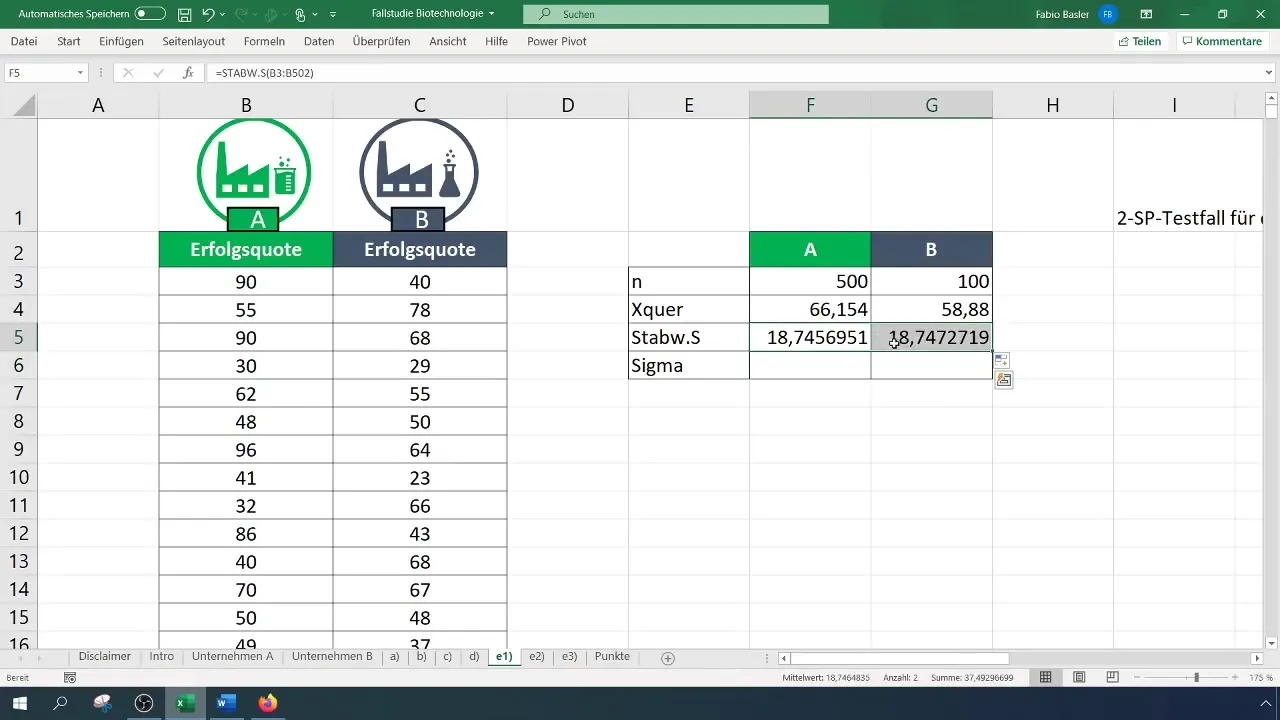
Krok 3: Obliczanie odchylenia standardowego
Oblicz odchylenie standardowe dla obu firm. Te wartości są istotne do przeprowadzenia dalszych obliczeń dotyczących wariancji.
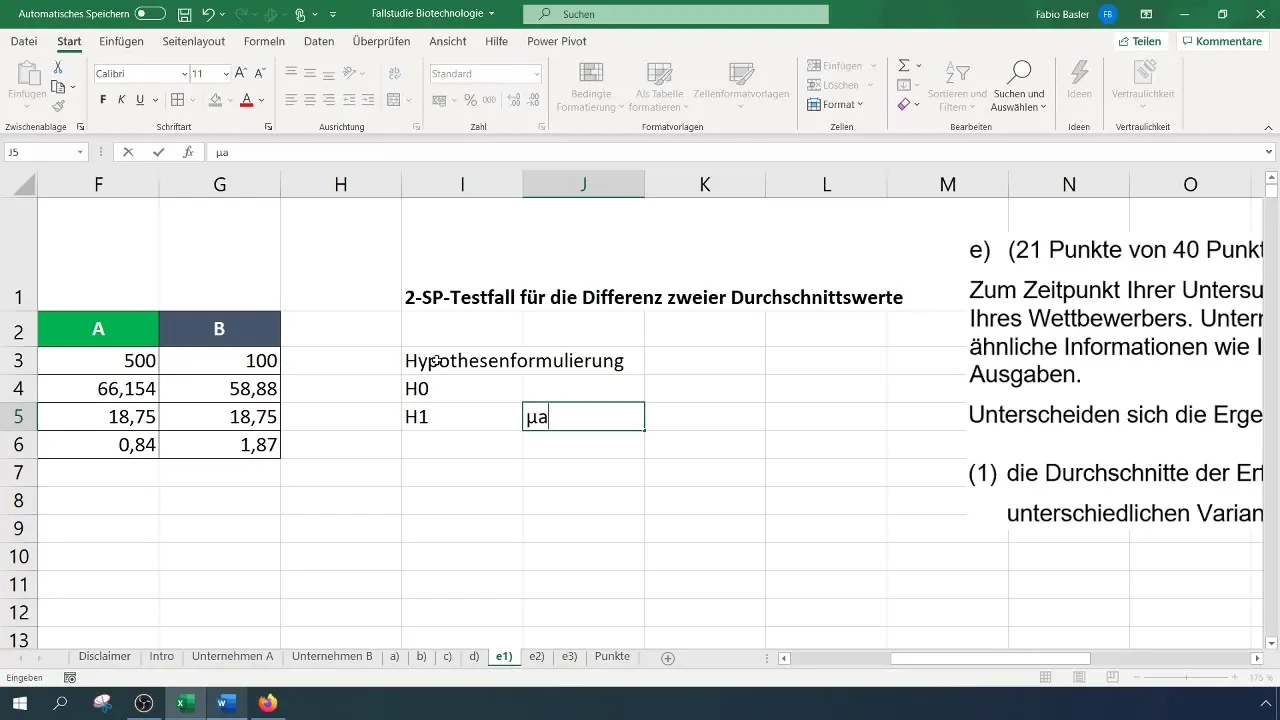
Krok 4: Formułowanie hipotez
Sformułuj hipotezę zerową (H_0): Średnie wskaźniki sukcesu firm A i B są równe. Hipoteza alternatywna (H_1): Średnie wskaźniki sukcesu są różne.
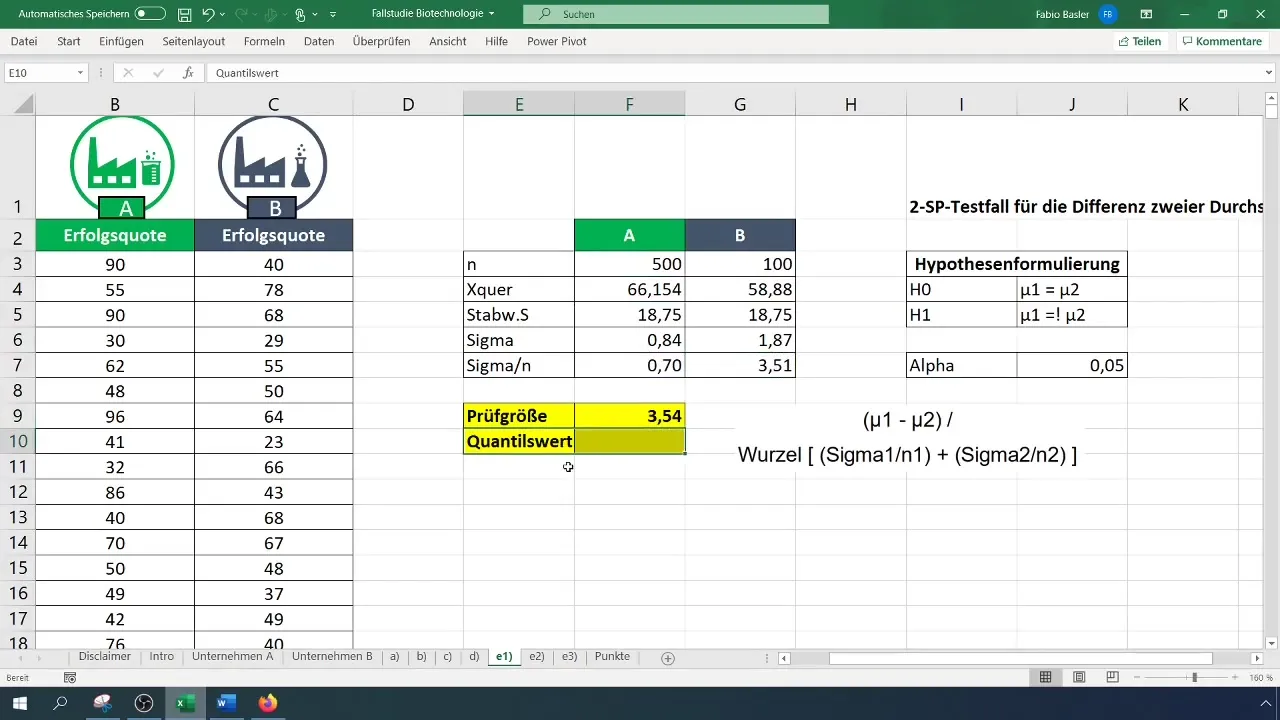
Krok 5: Obliczanie statystyki testowej
Aby obliczyć statystykę testową, skorzystaj z formuły dla testu t. Oblicz różnicę średnich i podziel ją przez pierwiastek sumy wariancji dla każdej próbki.
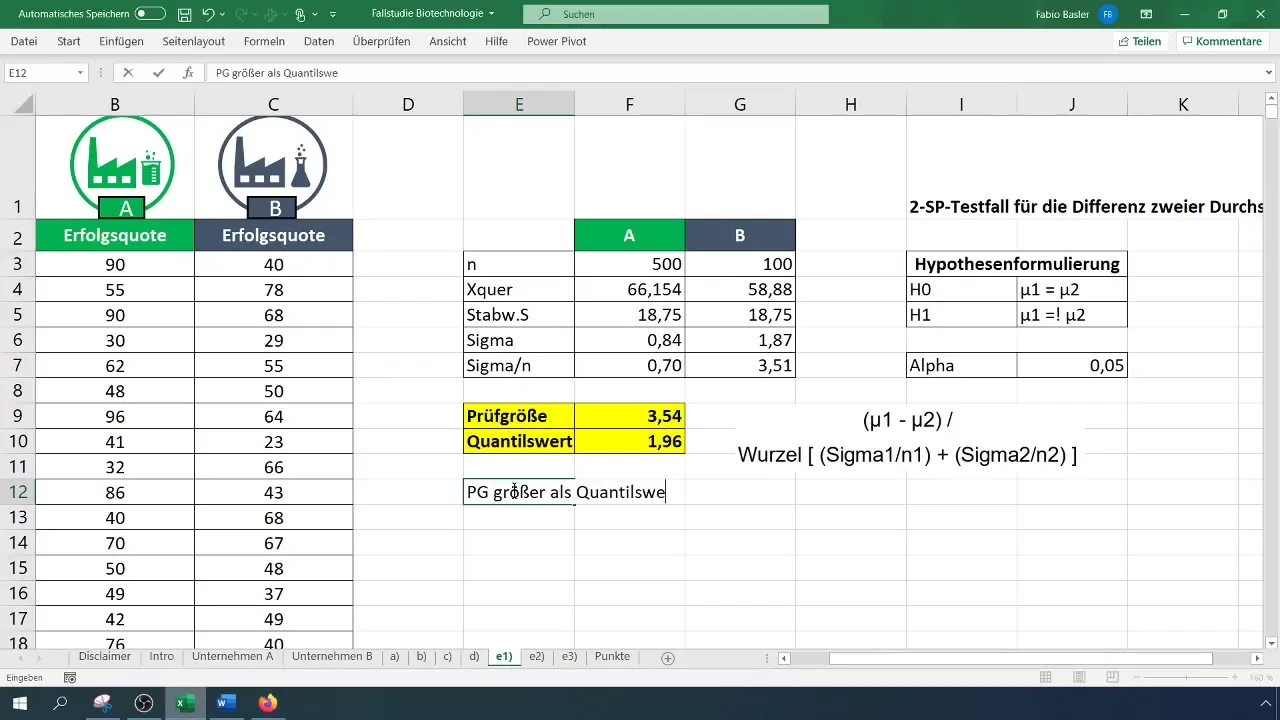
Krok 6: Określenie wartości krytycznej
Skorzystaj z dwustronnej dystrybucji t, aby znaleźć wartość krytyczną. Ustaw poziom alfa na 0,05. Sprawdź tabelę dystrybucji t lub oblicz wartość bezpośrednio w Excelu.
Krok 7: Podjęcie decyzji odnośnie hipotezy
Porównaj obliczoną statystykę testową z wartością krytyczną. Jeśli statystyka testowa jest większa niż wartość krytyczna, odrzuć hipotezę zerową (H_0) i potwierdź hipotezę alternatywną (H_1).
Krok 8: Interpretacja wyników
Ostatecznie zinterpretuj wyniki. W tym przykładzie stwierdzono istotną różnicę w średnich wskaźnikach sukcesu obu firm.
Podsumowanie
Dowiedziałeś się, jak przeprowadzić test dwóch prób niezależnych w Excelu dla zbadania różnic w średnich dwóch grup. Kluczowe są kroki od przygotowania danych przez formułowanie hipotez aż po interpretację wyników, aby podejmować trafne i świadome decyzje.
Najczęściej zadawane pytania
Czym jest test dwóch prób niezależnych?Test dwóch prób niezależnych porównuje średnie dwóch grup, aby stwierdzić, czy są istotnie różne.
Jak formułować hipotezy?Hipoteza zerowa (H_0) stwierdza, że średnie są równe, podczas gdy hipoteza alternatywna (H_1) zakłada, że są różne.
Jak obliczyć statystykę testową?Statystykę testową oblicza się poprzez podzielenie różnicy średnich przez pierwiastek sumy wariancji.
Co robić po wykonaniu obliczeń?Porównaj statystykę testową z wartością krytyczną, aby zdecydować, czy odrzucić hipotezę zerową.
Dlaczego odchylenie standardowe jest istotne?Odchylenie standardowe pomaga zrozumieć zmienność danych, co ma kluczowe znaczenie dla obliczenia statystyki testowej.


