Analizy statystyczne są niezbędnym narzędziem w zarządzaniu portfelem. Szczególnie potężną metodą jest analiza regresji, zwłaszcza gdy chodzi o określenie wpływu kilku zmiennych niezależnych na zmienną zależną. Chcesz dowiedzieć się, jak w programie Excel zbudować i zbadać związek liniowy poprzez regresję wieloraką? Niniejszy przewodnik zapewnia jasny przegląd oraz szczegółowe kroki do wykonania.
Najważniejsze wnioski
- Analiza regresji pomaga kwantyfikować wpływ zmiennych niezależnych na zmienną zależną.
- Ważne jest ocenienie jakości oraz istotności statystycznej modelu regresji.
- Ocena współczynników pozwala określić, która zmienna niezależna ma silniejszy wpływ na zmienną zależną.
Przewodnik krok po kroku do analizy regresji w Excelu
Przygotowanie danych
Przed rozpoczęciem analizy regresji musisz przygotować swoje dane. Zmienną zależną (y) w tym przypadku jest sprzedaż notebooków, a zmienne niezależne (x1 i x2) to liczba pracowników oraz liczba działań konkurencyjnych. Po pierwsze, wprowadź wszystkie wymagane dane do programu Excel i uporządkuj je w przejrzysty sposób.
Sprawdzenie korelacji
Aby uzyskać pierwsze wskazówki na temat możliwych związków między zmiennymi, możesz utworzyć macierz korelacji. Ta macierz pomaga zobaczyć, jak silnie zmiennie są ze sobą powiązane. Możesz to zrobić poprzez funkcję „Analiza danych” w Excelu, a następnie wybrać macierz korelacji, uwzględniając wszystkie istotne obszary danych.
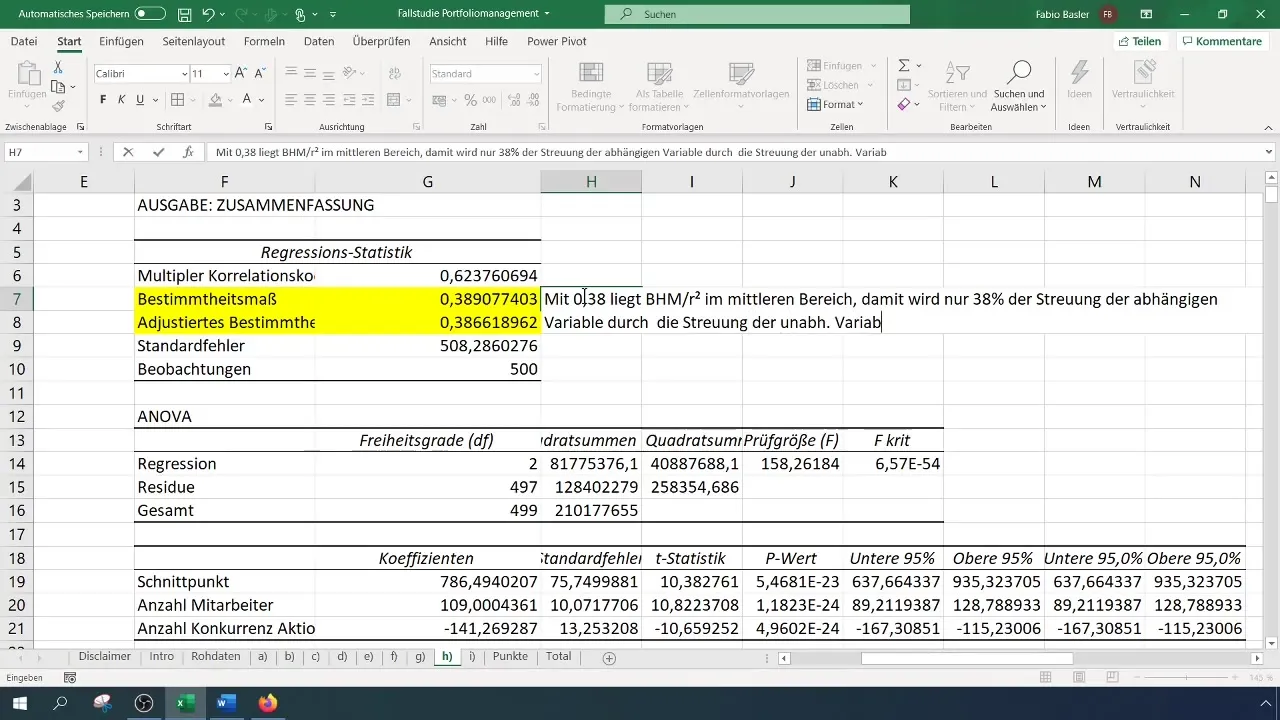
Przeprowadzenie analizy regresji
Teraz jesteś gotowy do przeprowadzenia analizy regresji. Ponownie wybierz funkcję „Analiza danych”, a następnie wybierz „Regresja”. Tutaj podajesz zakres wejściowy dla zmiennej zależnej (sprzedaż notebooków) oraz zmiennych niezależnych (liczba pracowników i działań konkurencyjnych).
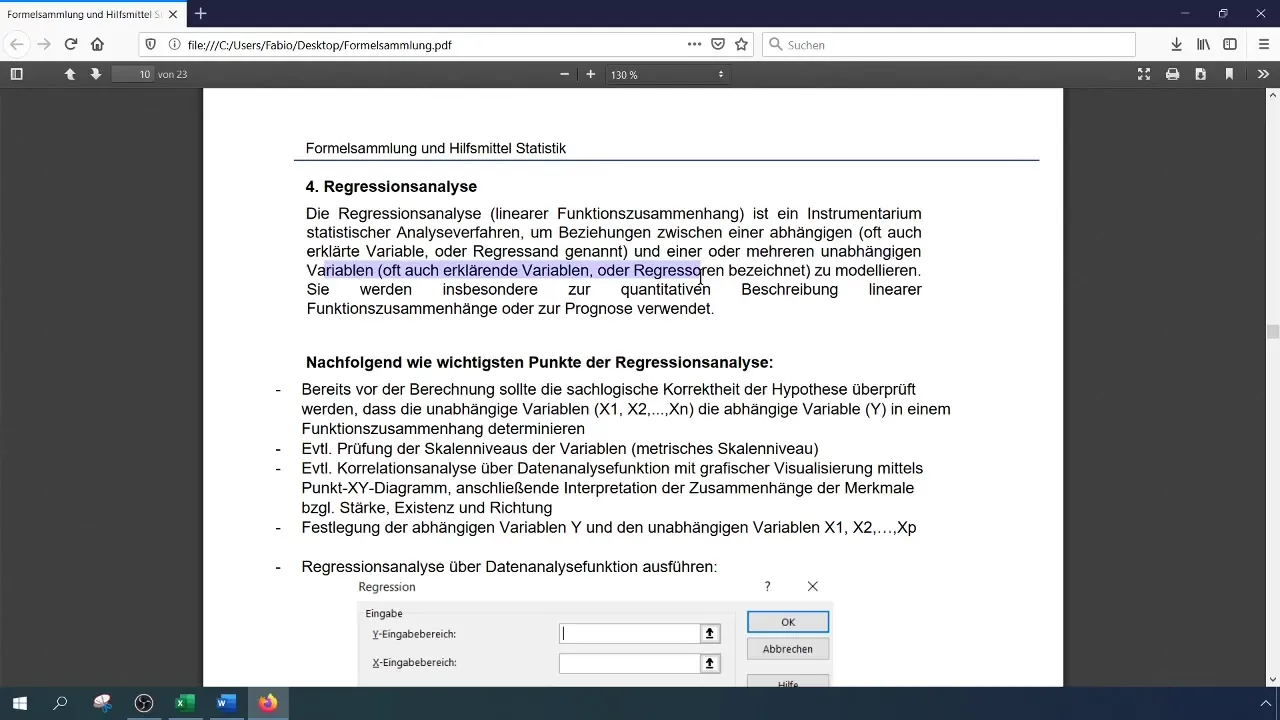
Interpretacja wyników
Po przeprowadzeniu analizy regresji otrzymasz wiele wyników i statystyk. Pierwszym ważnym punktem jest miara determinacji (R²), która opisuje procent wyjaśnienia zmienności zmiennej zależnej przez zmienne niezależne. Wartość R² wynosząca 0,38 oznacza, że 38% zmienności w sprzedaży może być wyjaśnione przez obie zmienne niezależne.
Podczas analizy zwróć uwagę na stabilność modelu. Możesz zastosować błąd standardowy do oceny stabilności. Na przykład otrzymując błąd standardowy na poziomie 0,51, oznacza to wysoką względną zmienność i tym samym niską stabilność.
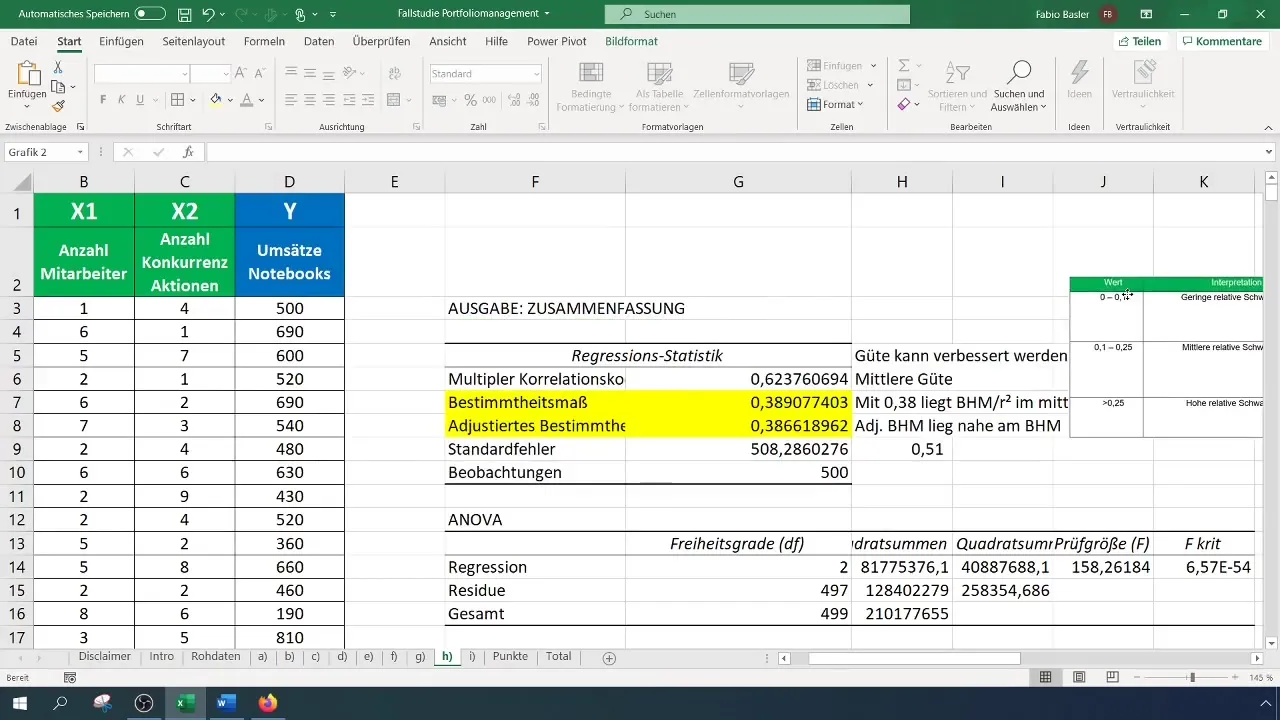
Ocena silnych czynników wpływu
Istotnym krokiem jest ustalenie, która z zmiennych niezależnych ma silniejszy wpływ na zmienną zależną. Możesz to zrobić, korzystając z współczynników, które określają bezwzględną istotność zmiennych. Współczynnik x1 (Liczba pracowników) wynosi 109, podczas gdy współczynnik x2 (Liczba działań konkurencyjnych) wynosi -141. Oznacza to, że zwiększenie liczby pracowników zwiększy sprzedaż o 109 euro, natomiast zwiększenie działań konkurencyjnych zmniejszy sprzedaż o 141 euro.
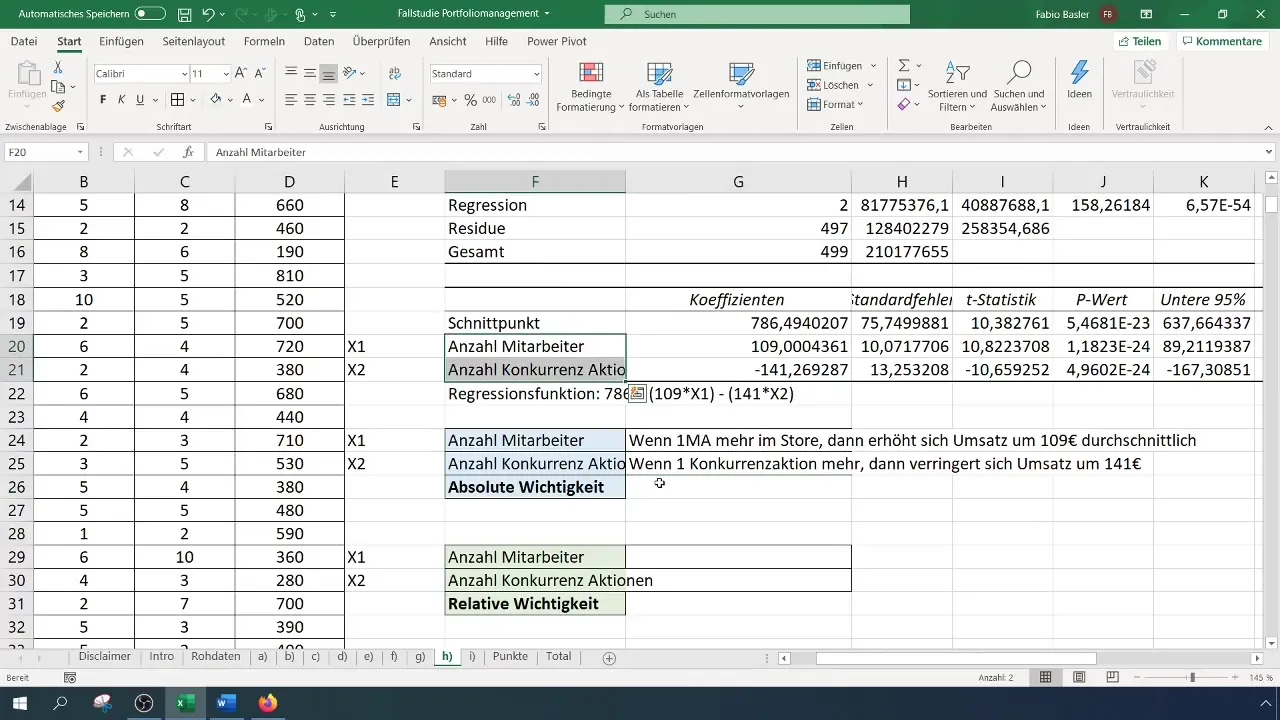
Ocena istotności statystycznej
Kolejnym istotnym aspektem analizy regresji jest istotność statystyczna. Możesz to zobaczyć na podstawie wartości p oraz testu F, które powinny być bardzo małe. Oznacza to, że zmienne niezależne mają istotny wpływ na zmienną zależną i uzasadnia to użycie modelu.
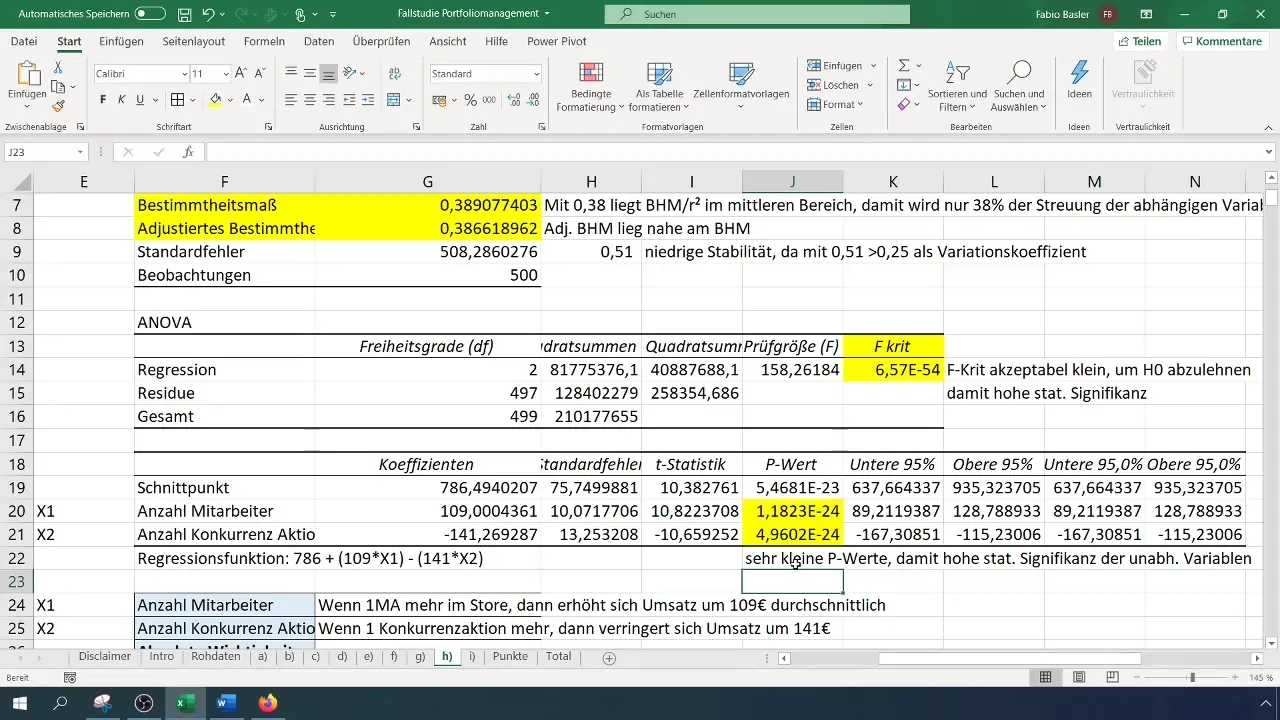
Podsumowanie
Analiza regresji w programie Excel pozwala zrozumieć związek między różnymi zmiennymi w sposób ilościowy. Dzięki tej instrukcji poznajesz kroki do przeprowadzenia i interpretacji regresji wielorakiej. Bądź uważny na jakość i stabilność modelu oraz oceniaj poszczególne czynniki wpływu krytycznie, aby podejmować merytoryczne decyzje w zarządzaniu portfelem.
Najczęściej zadawane pytania
Welche Daten benötige ich für die Regressionsanalyse?Potrzebujesz zmiennej zależnej (np. przychód) i co najmniej jednej lub kilku zmiennych niezależnych (np. liczba pracowników, działania konkurencji).
Jak interpretować wskaźnik determinacji R²?Wyższa wartość R² oznacza, że większy odsetek zmienności w zmiennej zależnej jest wyjaśniany przez zmienne niezależne.
Jak sprawdzić istotność statystyczną?Możesz skorzystać z wartości p (p-wartości) i testu F; niskie wartości wskazują na wysoką istotność.
Jaka jest różnica między R² a skorygowanym R²?Skorygowane R² uwzględnia liczbę zmiennych niezależnych i zapewnia bardziej realistyczną ocenę w przypadku modeli z wieloma zmiennymi.
Jak oszacować siłę czynników wpływających?Dzieje się to przez ocenę współczynników zmiennych niezależnych, które kwantyfikują wpływ każdej zmiennej na zmienną zależną.


