Możliwość korzystania z narzędzi analizy danych w Excelu jest kluczowa dla sukcesu w biznesie i sprzedaży. Niniejszy przewodnik skupia się na analizie korelacji i regresji, aby dowiedzieć się, jak liczba pracowników i liczba rozmów telefonicznych wpływają na obroty. Przeprowadzenie obu analiz pomoże Ci ocenić te zależności ilościowo i zrozumieć interpretację wyników.
Najważniejsze wnioski
- Rożnica między korelacją a regresją: korelacja pokazuje zależność między dwiema zmiennymi, podczas gdy regresja badaża wpływ kilku niezależnych zmiennych na zmienną zależną.
- Pogląd na statystyczną istotność oraz jakość modelu.
- Ocena ilościowa ważności regresów.
Przewodnik krok po kroku
1. Przygotowanie do analizy danych
Przed rozpoczęciem analizy upewnij się, że Twoje dane są poprawnie przygotowane w Excelu. Zaimportuj dane dotyczące obrotu, liczby pracowników i rozmów telefonicznych do arkusza Excela. Upewnij się, że wszystkie rekordy danych są kompletne, a wymagane zmienne są obecne.

2. Przeprowadzenie analizy korelacji
Aby zanalizować korelację między zmiennymi obrotu, pracowników i rozmów telefonicznych, możesz obliczyć wspołczynnik korelacji. Do tego celu używaj formuły =KOREL() w Excelu. Aby uzyskać przegląd wszystkich zmiennych, stwórz macierz korelacji.
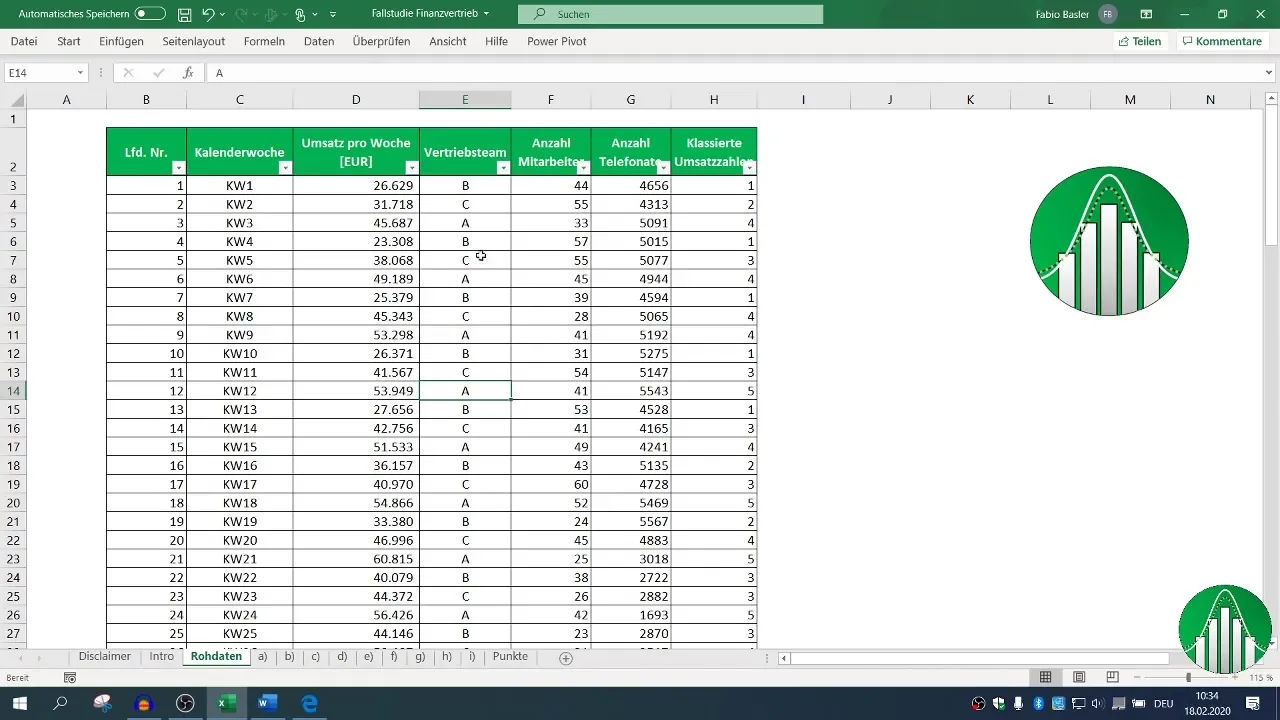
Najpierw zaznacz odpowiednie kolumny dla obrotu i liczby pracowników. Za pomocą formuły =KOREL( zaznacz obszary dla obrotu i liczby pracowników. Wynik pokaże, jak silna jest zależność.
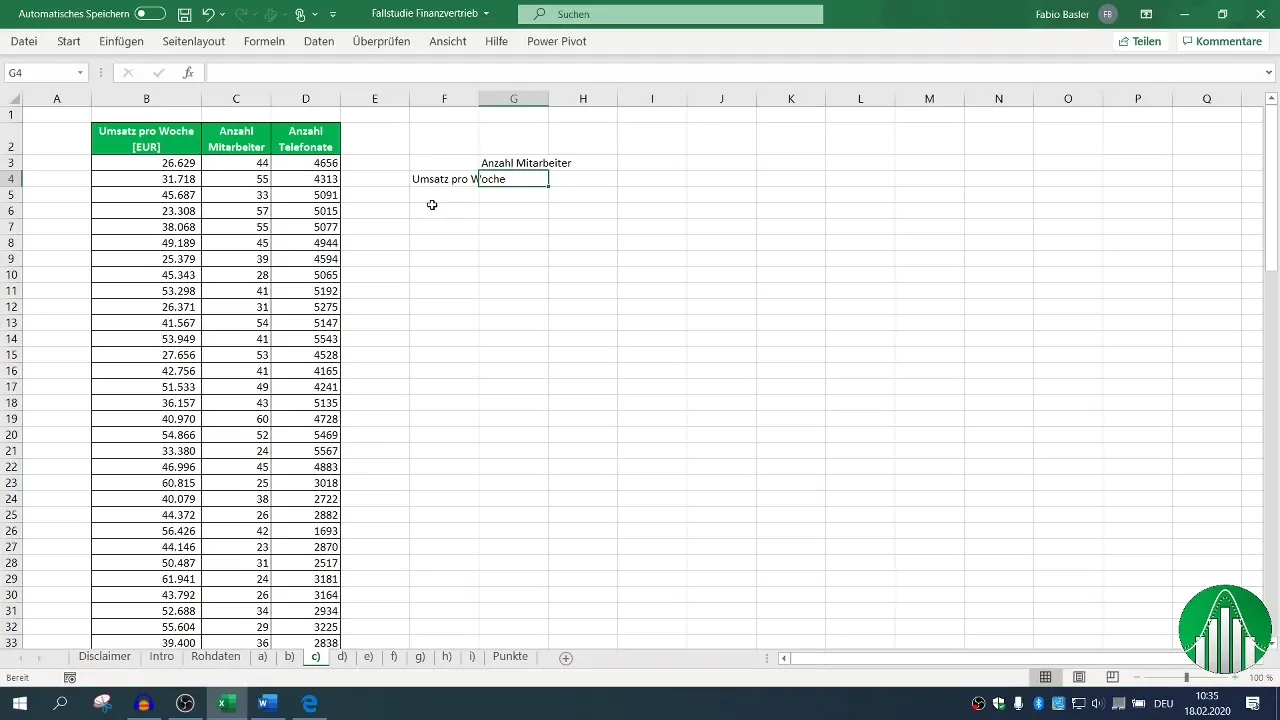
3. Stworzenie macierzy korelacji
Do bardziej kompleksowej analizy zalecane jest używanie funkcji analizy danych w Excelu. Aktywuj funkcję analizy danych, jeśli jeszcze tego nie zrobiłeś. Przejdź do zakładki "Dane", kliknij "Analiza danych" i wybierz "Korelacja".
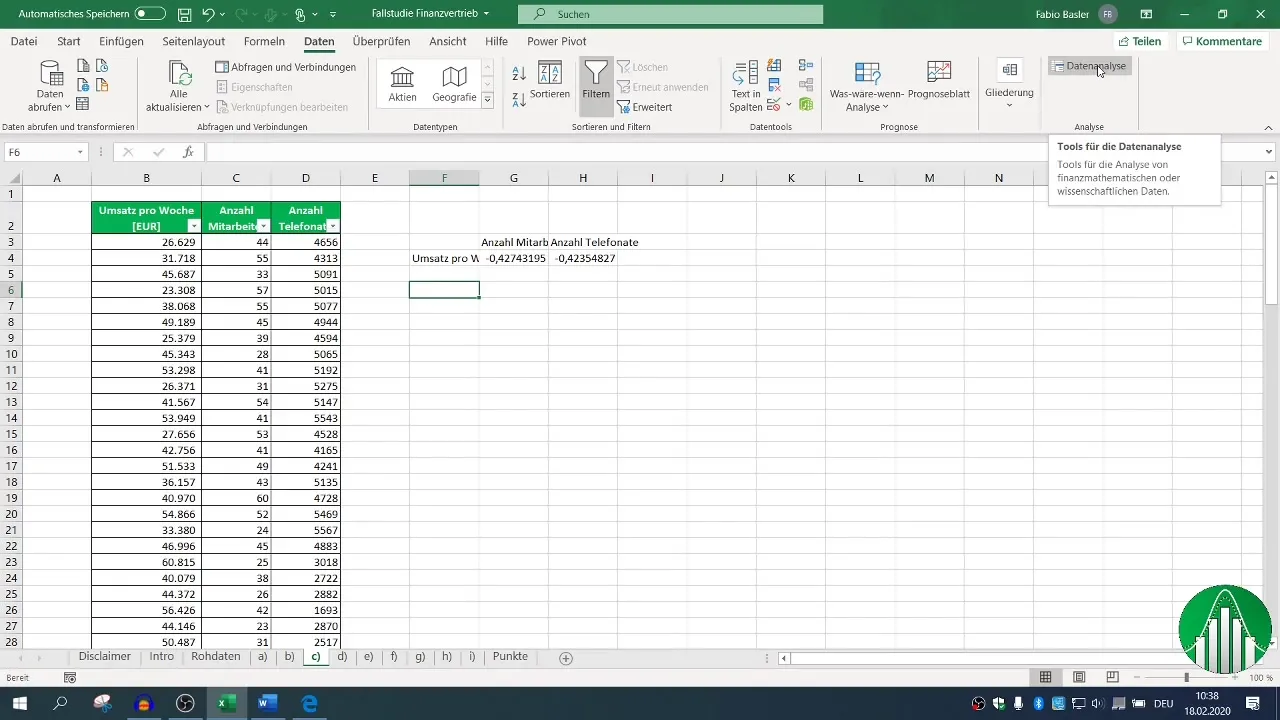
Zdefiniuj przedział wejściowy dla Twoich danych i zaznacz pole wyboru dla nagłówka, aby Excel poprawnie rozpoznał etykiety. Po skonfigurowaniu obszaru wyjściowego możesz generować macierz korelacji, która pokaże wszystkie istotne zależności.
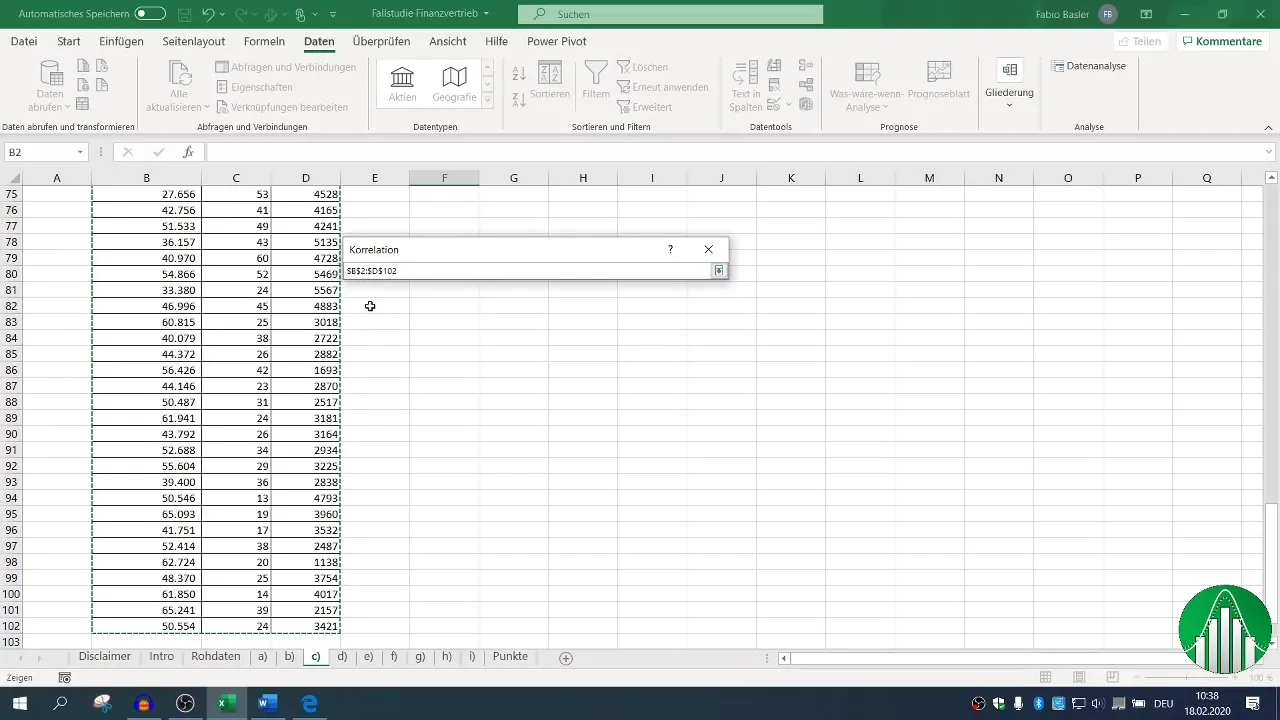
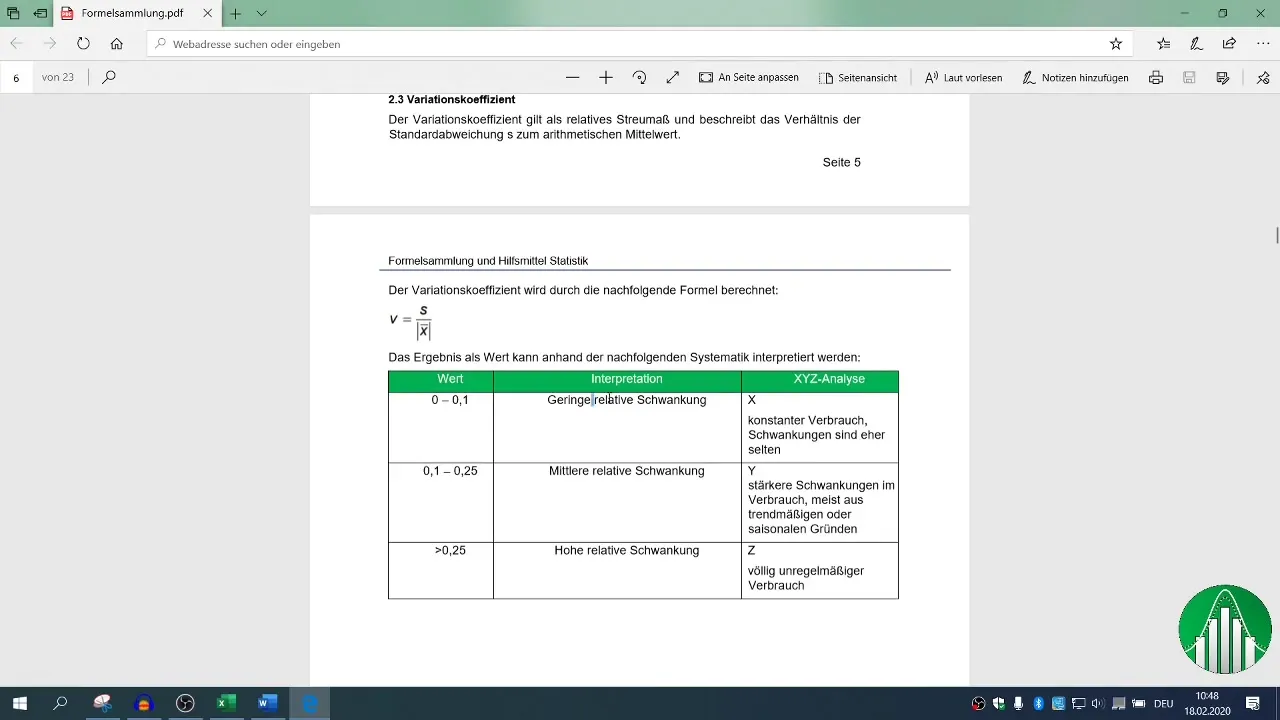
4. Wizualizacja korelacji
Aby uczynić wyniki bardziej przystępnymi, może być przydatna graficzna reprezentacja poprzez diagram XY. Wybierz swoje dane X i Y i wygeneruj chmurę punktów.
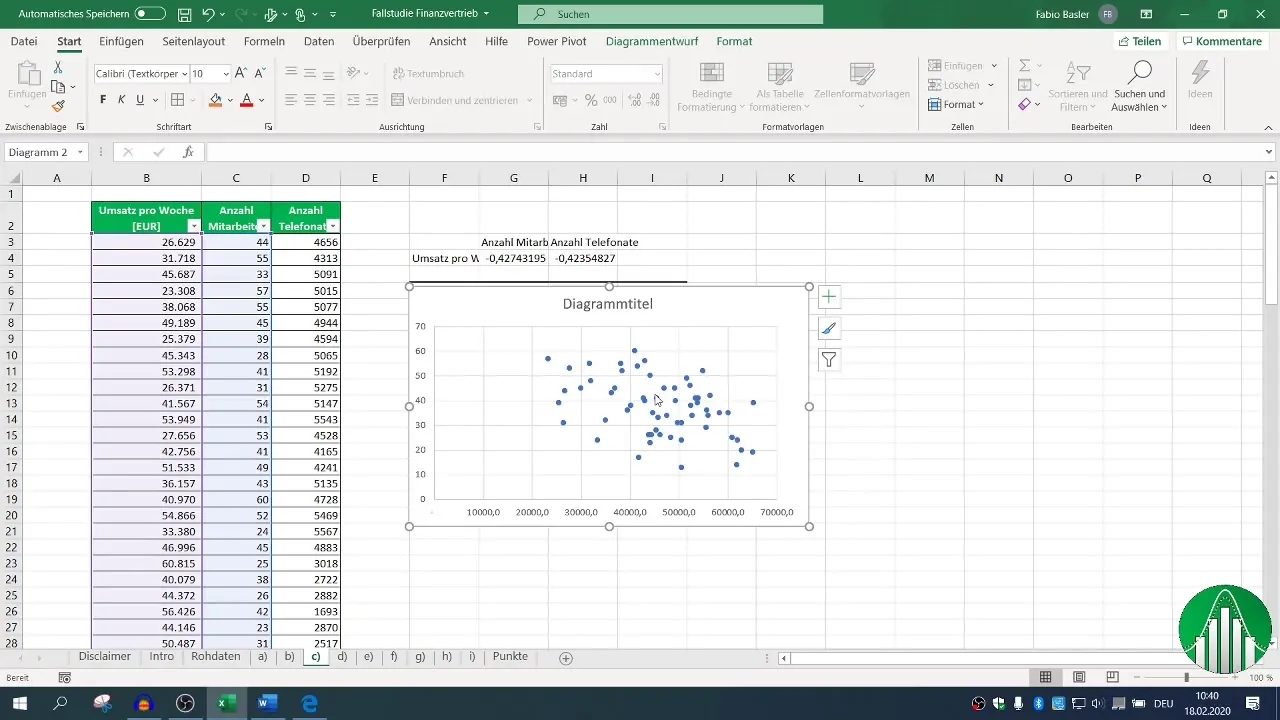
Dodaj linię trendu, aby wizualnie przedstawić zależność. Może to oferować bardziej intuicyjne zrozumienie danych.
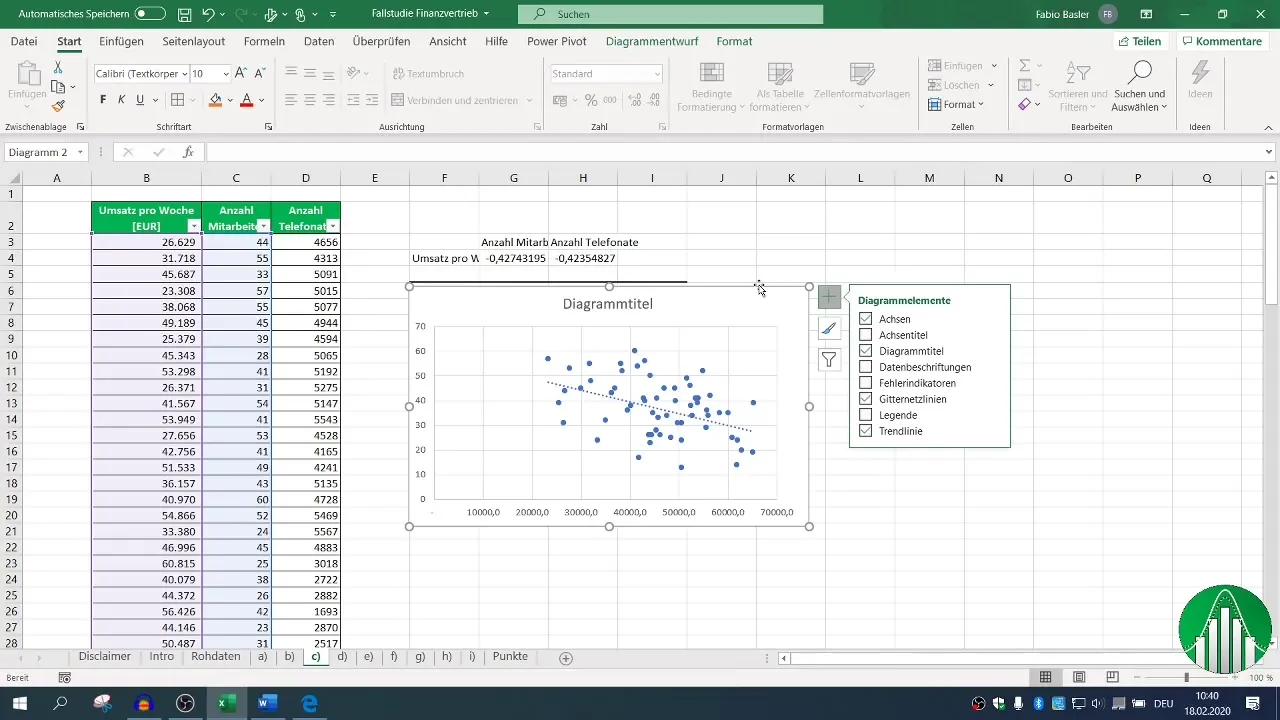
5. Przeprowadzenie analizy regresji
Następnie przejdź do analizy regresji. Ponownie wejdź w "Dane" i wybierz "Analiza danych", a następnie "Regresja". Możesz zdefiniować dla obszaru wejściowego zmienną zależną (obroty) i niezależne zmienne (liczba pracowników i rozmowy telefoniczne).
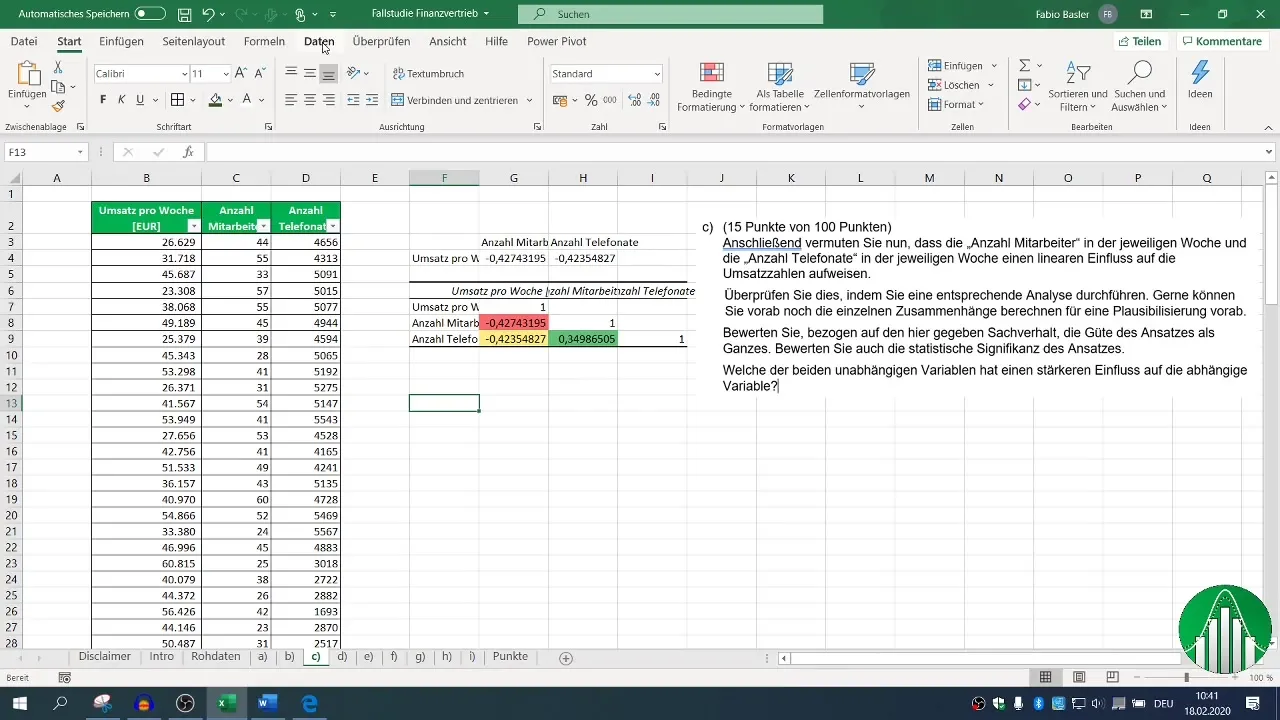
Upewnij się, że tytuł dla wartości jest ustawiony i zdefiniuj obszar wyjściowy. Standardowy poziom ufnnosć jest ustawiony na 95%, co jest wystarczające dla większości analiz.
6. Ocena analizy regresji
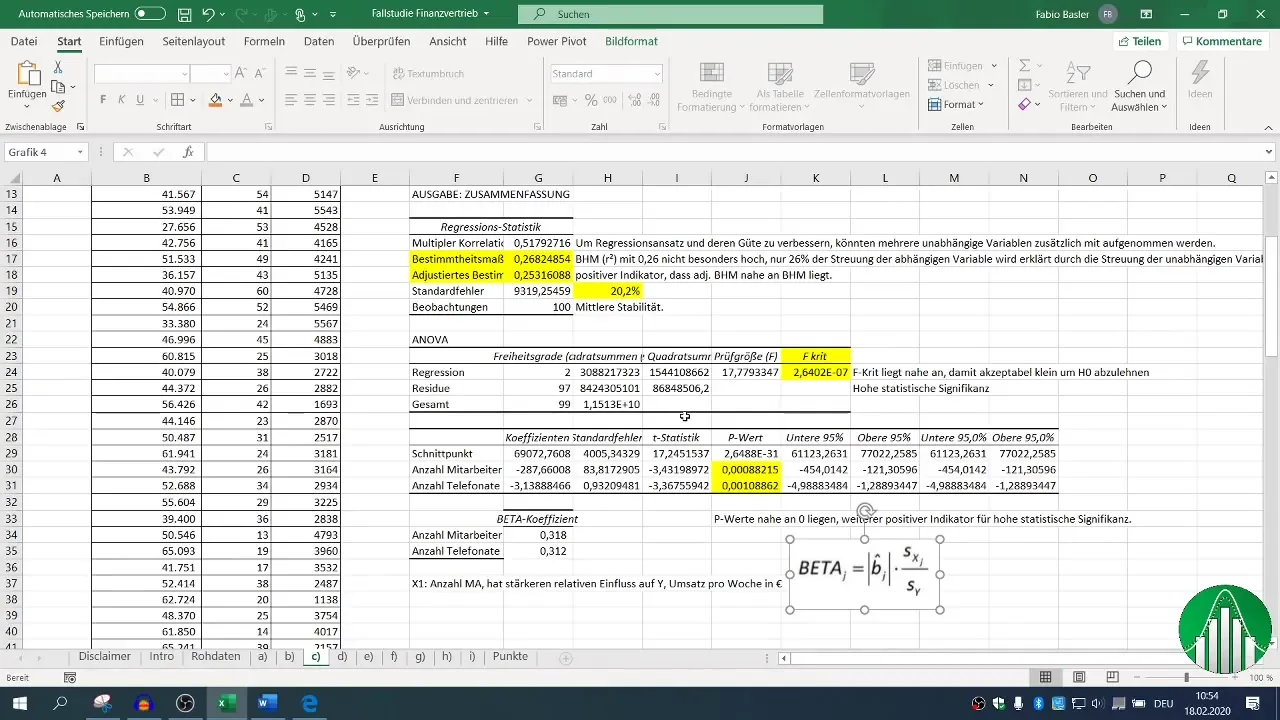
Po przeprowadzeniu regresji masz różne bloki wyników do dyspozycji. Skup się na miarze determinacji (R²), która opisuje jakość modelu. R² wynoszące 0,26 oznacza, że jedynie 26% zmienności obrotu jest wyjaśnione przez niezależne zmienne.
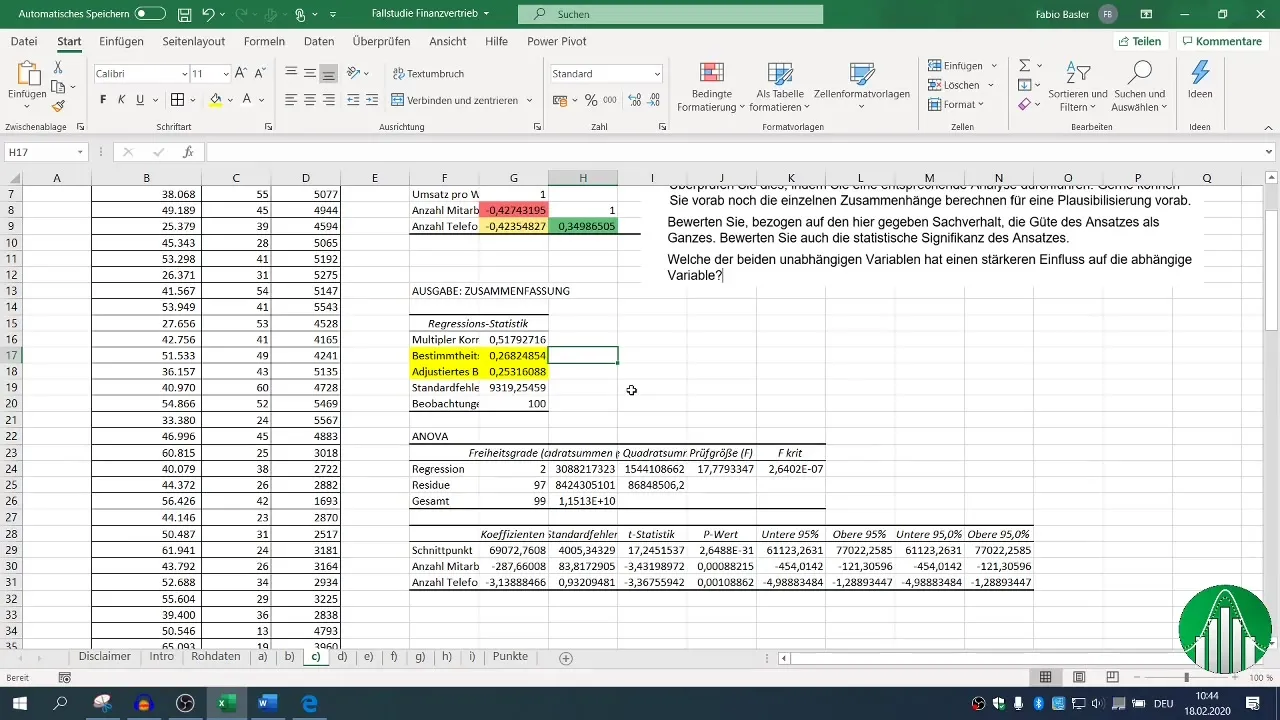
Wskaźnik determinacji dostosowany powinien być bliski R², co w tym przypadku jest pozytywnym wskaźnikiem.
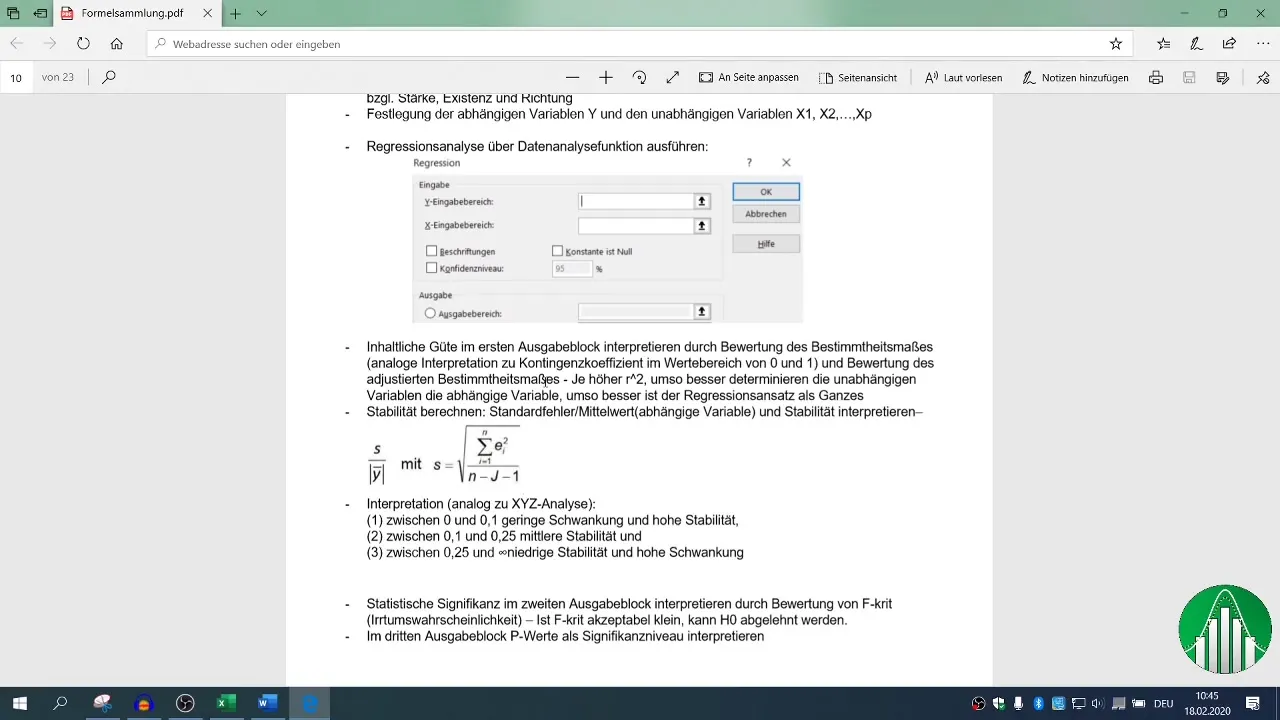
Ocena znaczenia statystycznego
Wartość F i wartości p niezależnych zmiennych są decydujące przy ocenie znaczenia statystycznego Twojego modelu. Wartość p poniżej 0,05 wskazuje na istotność statystyczną związku.
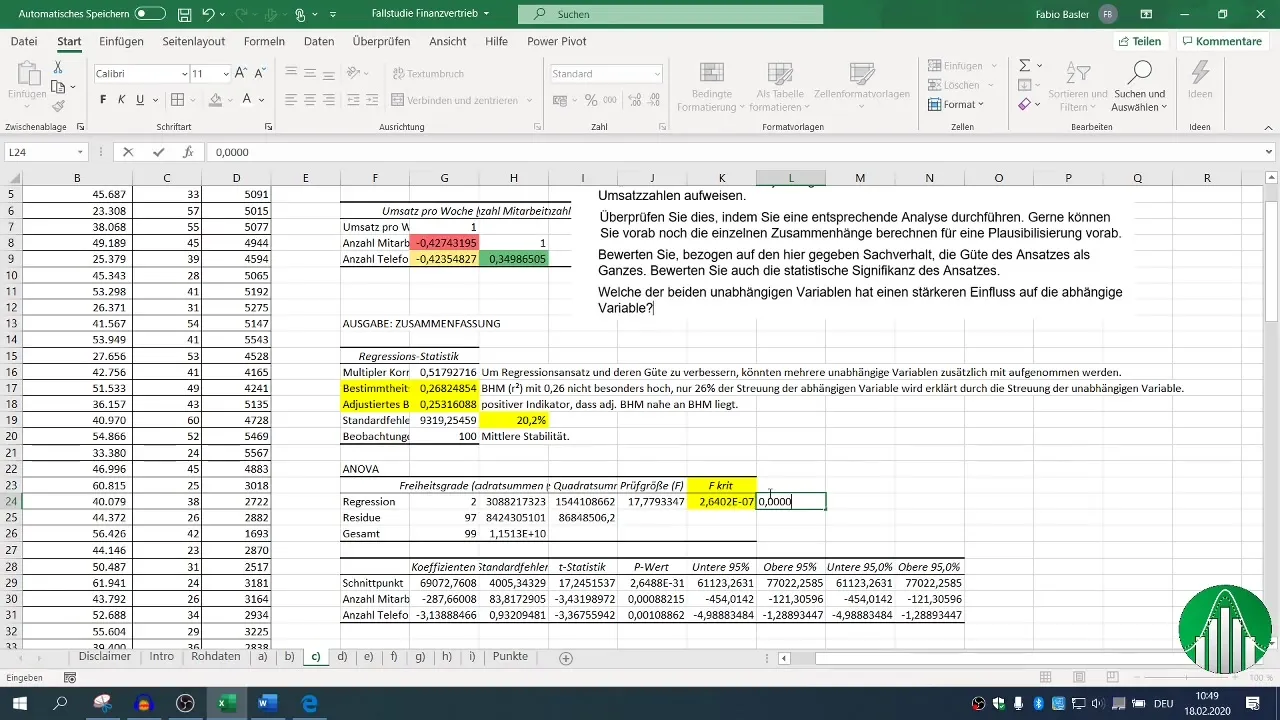
Ocena tych wskaźników statystycznych w kontekście R² pomoże Ci zrozumieć stabilność i siłę przekazu swoich wyników.
Porównanie czynników wpływu
Ostatecznie interesuje Cię, który czynnik – liczba pracowników czy rozmowy telefoniczne – ma silniejszy wpływ na wyniki sprzedażowe. W tym celu sięgasz po współczynniki beta i porównujesz je.
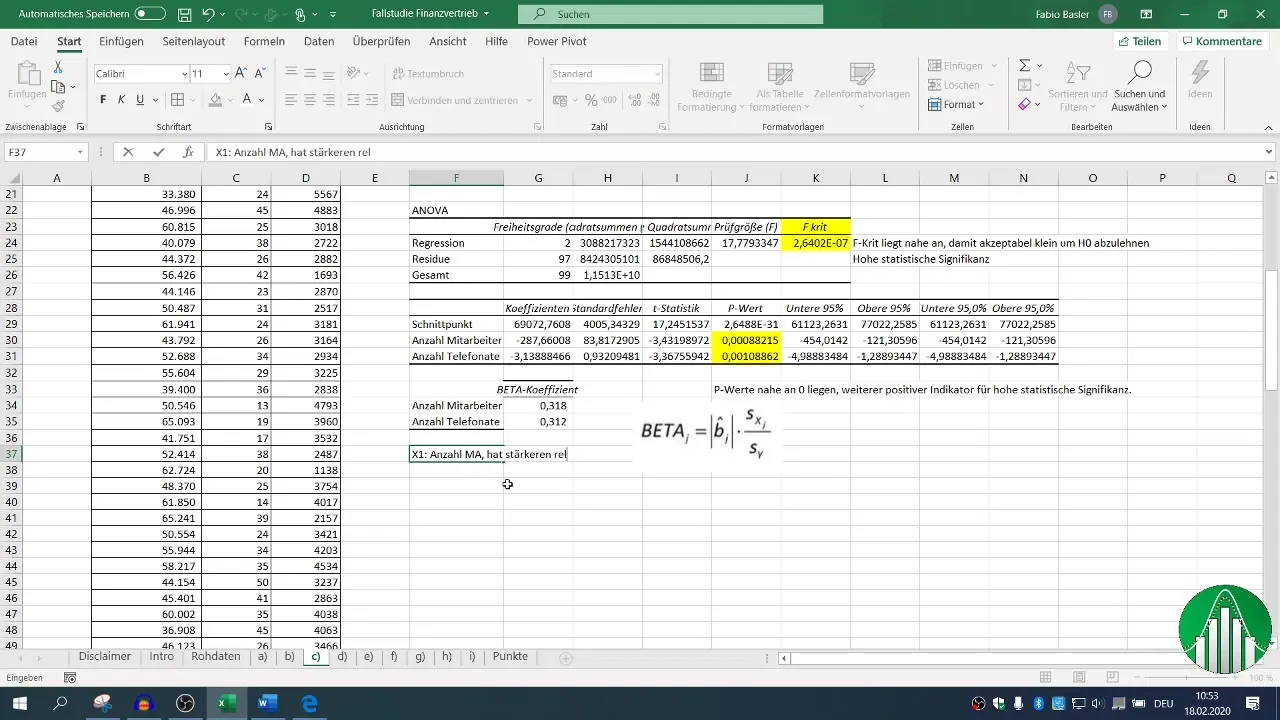
Wyższy współczynnik beta wskazuje na względny wpływ; możliwe, że liczba pracowników ma większy wpływ na sprzedaż niż liczba rozmów telefonicznych.
Podsumowanie
Poprzednia analiza dała Ci cenne wglądy w statystyczne relacje między zmiennymi sprzedaż, liczbą pracowników i rozmowami telefonicznymi. Systematyczne przeprowadzanie analiz korelacji i regresji w Excelu pozwala podejmować uzasadnione decyzje oparte na Twoich wynikach.
Najczęściej zadawane pytania
Dlaczego analiza korelacji jest ważna?Analiza korelacji pomaga zauważyć związek między dwiema zmiennymi, zanim przeprowadzone zostanie szczegółowe analiza regresji.
Jak interpretować R² w analizie regresji?Wartość R² wynosząca 0,26 oznacza, że 26% zmienności zmiennej zależnej (sprzedaż) jest wyjaśnione przez zmienne niezależne.
Jaka jest różnica między korelacją a regresją?Korelacja mierzy związek między dwiema zmiennymi, podczas gdy regresja ocenia wpływ kilku zmiennych niezależnych na zmienną zależną.
Jak można przetestować istotność statystyczną?Testujesz istotność statystyczną na podstawie wartości p; wartości p poniżej 0,05 są uznawane za istotne.
Jaka jest rola współczynników beta?Współczynniki beta pokazują względny wpływ zmiennych niezależnych na zmienną zależną.


