Analizy korelacyjne rang są kluczową częścią statystycznego badania zależności między zmiennymi. W szczególności, gdy mamy do czynienia z danymi o skalach porządkowych, korelacja d’alexa jest wartościową metodą do rozpoznawania wzorców i związków. W tym samouczku krok po kroku dowiesz się, jak obliczyć korelację rangową D'Alemberta dla ankiety za pomocą Excela.
Ważne spostrzeżenia
- Korelacja rang mierzy siłę i kierunek monotonicznej relacji między dwoma zmiennymi porządkowymi.
- Współczynnik korelacji rang Spearmana jest szczególnie odpowiedni, gdy jedna zmienna jest porządkowa, a druga metryczna.
- Obliczenia w Excelu można przeprowadzić za pomocą prostych wzorów i funkcji.
Przewodnik krok po kroku
Najpierw definiujemy zmienne, które chcemy zbadać. Tutaj mamy do czynienia z satysfakcją klientów (zmienna porządkowa, wartości 1-3) i liczbą zamówień (skalowana metrycznie).
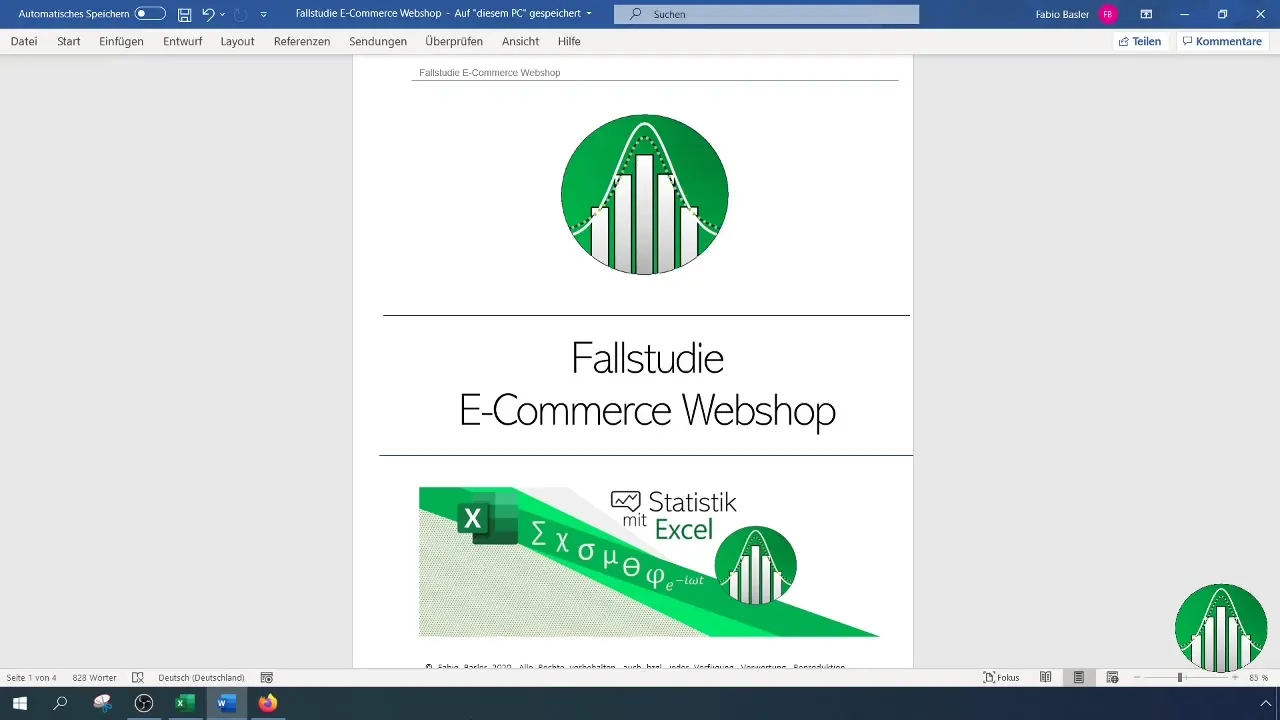
Aby utworzyć ranking dla satysfakcji i liczby zamówień, potrzebujesz tabeli zawierającej odpowiednie dane. Upewnij się, że wpisujesz te dane w Excelu.

Po wprowadzeniu danych do Excela, przejdziemy do obliczenia korelacji rangowej D'Alemberta. Do tego celu użyjemy funkcji „Rang.Mittel” w Excelu, która zwraca rangę liczby w liście. Dla satysfakcji zastosujemy początkowo wzór:
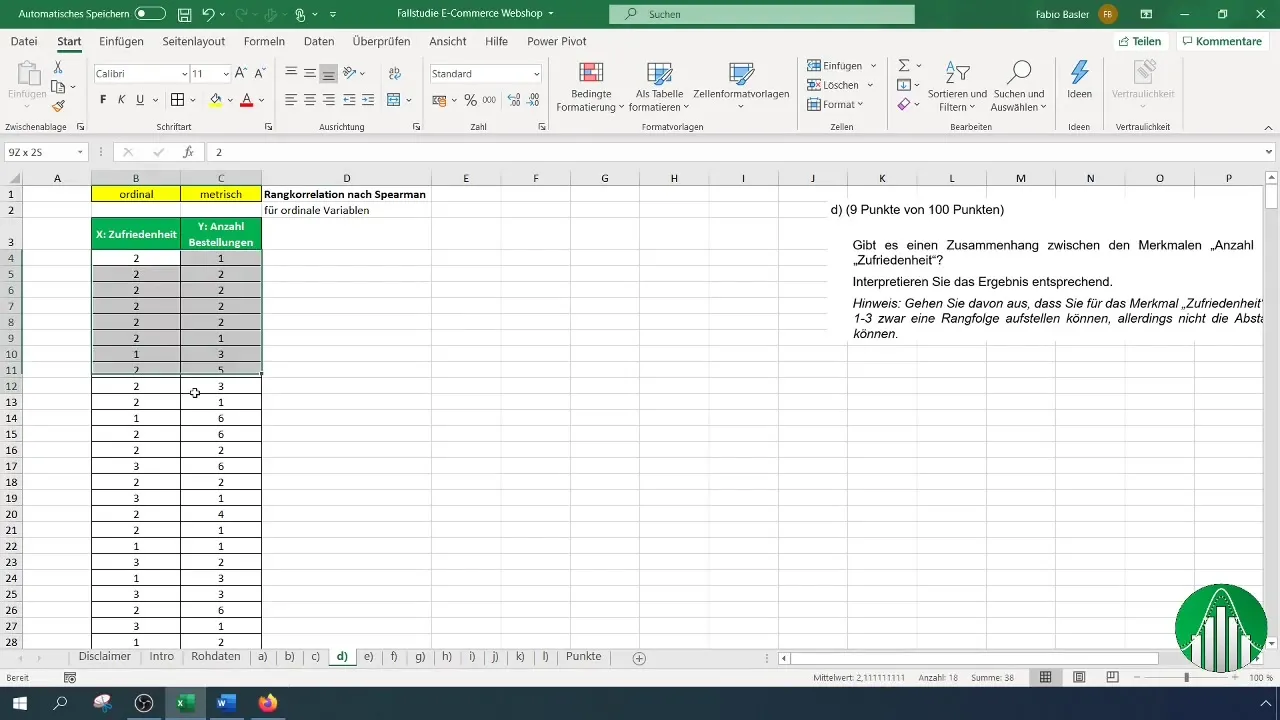
Pamiętaj, że przy stosowaniu tego wzoru musisz zaznaczyć kolumnę satysfakcji i określić cały zakres od B4 do końca swojej serii danych, aby poprawnie zidentyfikować rangi.
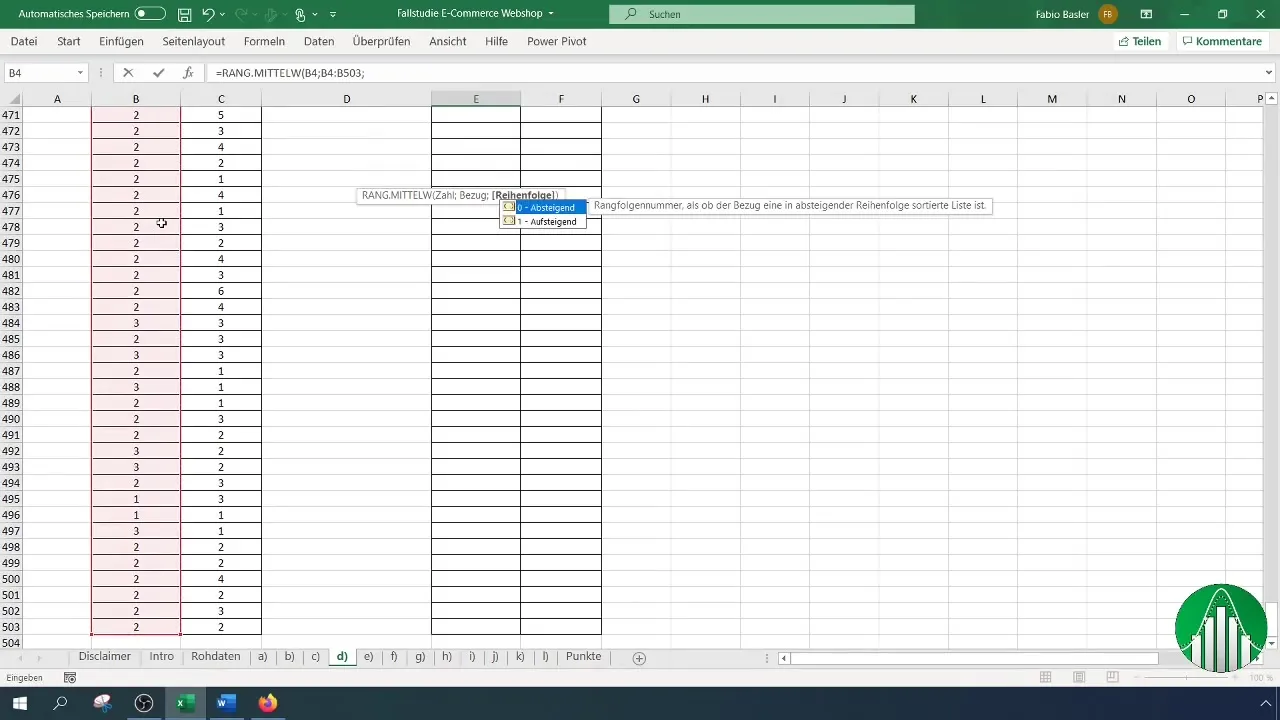
Zdecyduj, czy chcesz posortować rangi rosnąco czy malejąco. Zazwyczaj zaleca się sortowanie rosnące. Podkreśl, że odniesienia komórek na rangi są stałe, używając klawisza F4. Jest to ważne, aby uniknąć zmiany odniesień podczas kopiowania.
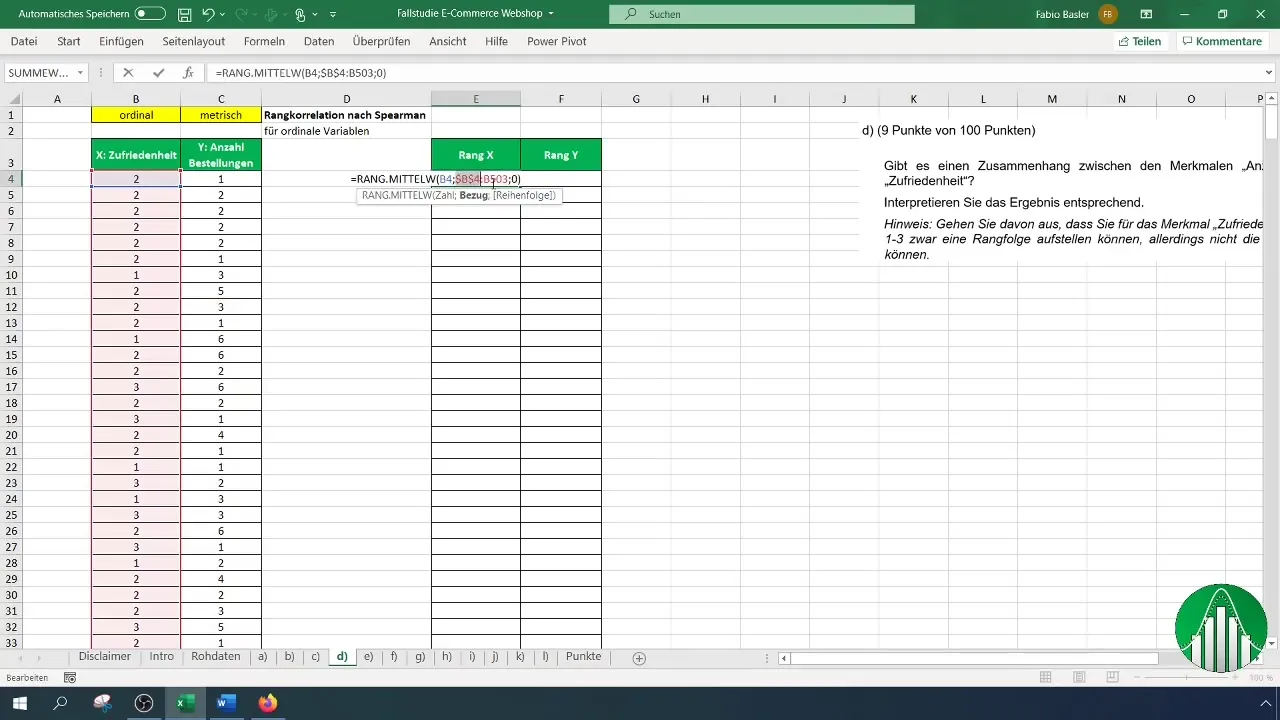
Po ustaleniu rang dla satysfakcji, powtórz proces dla liczby zamówień. Upewnij się, że poprawnie stosujesz wzór i odniesienie.
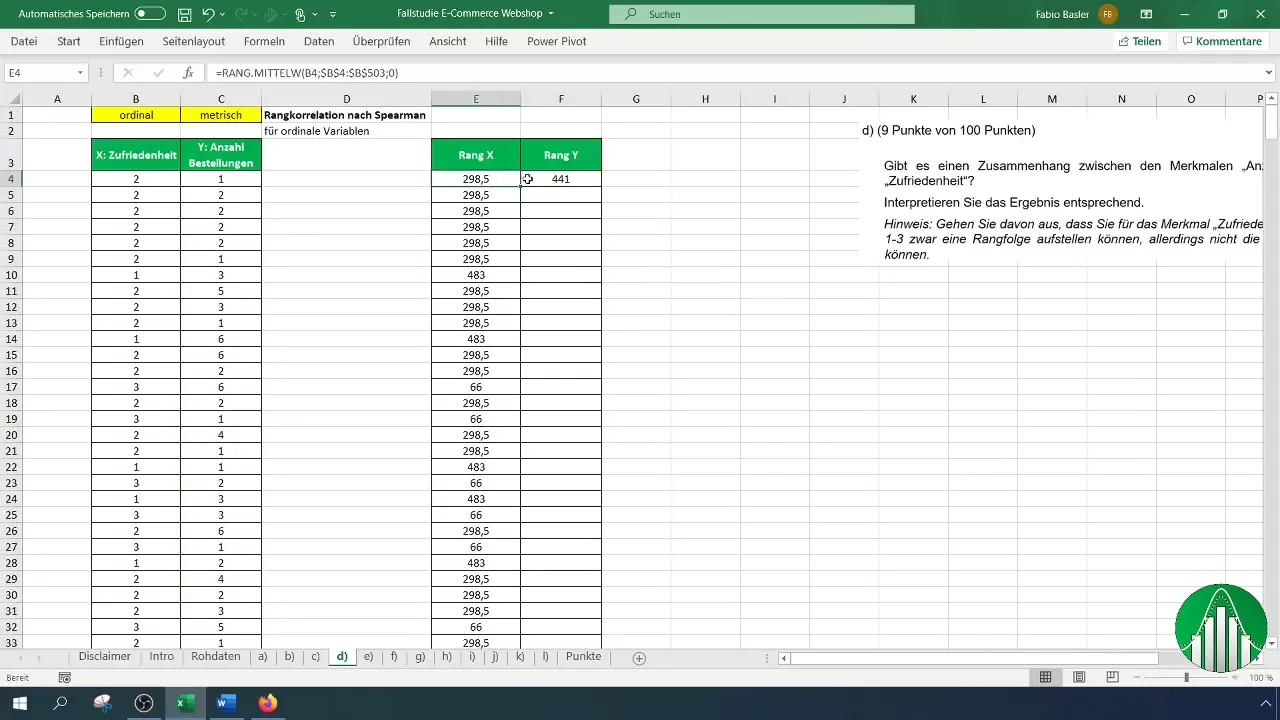
Mając obie listy rankingowe (satysfakcja i liczba zamówień), jesteś gotowy do obliczenia współczynnika korelacji rangowej D'Alemberta. W tym celu użyjesz wzoru "=KOREL", aby określić związek. Składnia wygląda następująco:
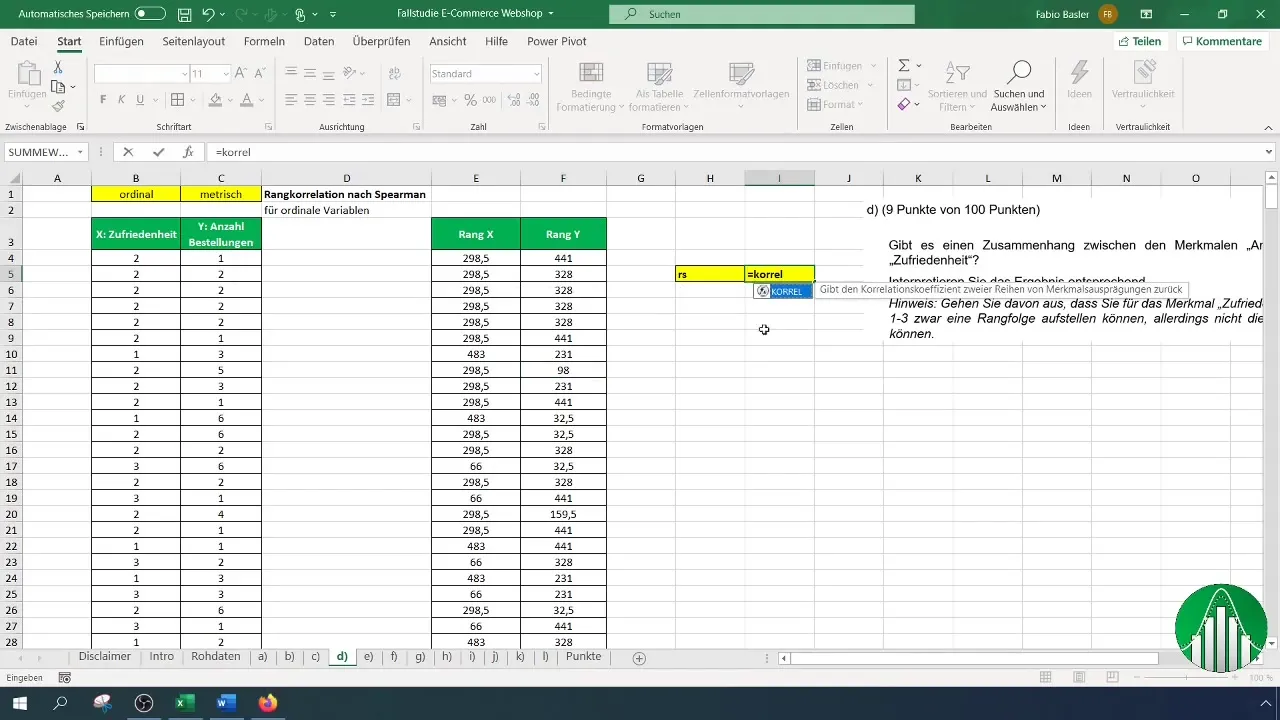
Dla pierwszego odniesienia podaj listę rang satysfakcji, a dla drugiego listę zamówień. Excel automatycznie obliczy współczynnik korelacji rangowej D'Alemberta.

Jaki jest wynik twojego obliczenia? Wartość 5,61% wskazuje na słabe pozytywne powiązanie między satysfakcją a liczbą zamówień. Oznacza to, że istnieje niewielki związek między tymi dwiema zmiennymi.
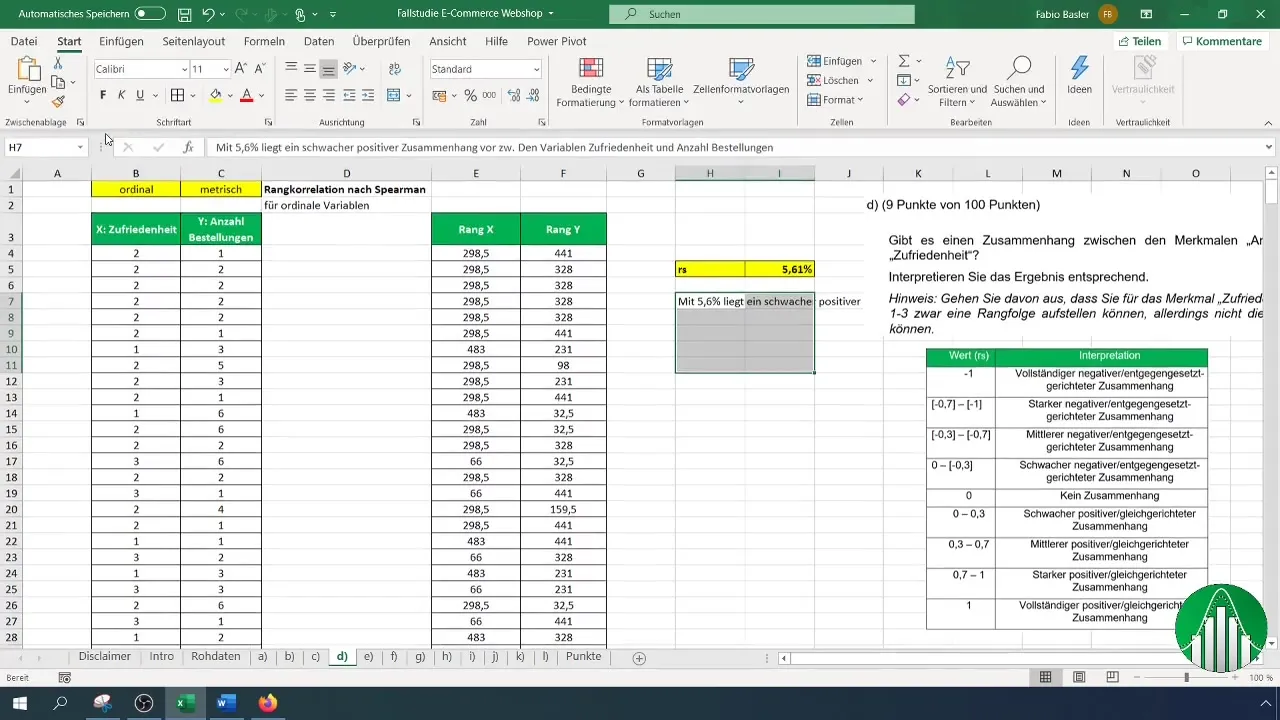
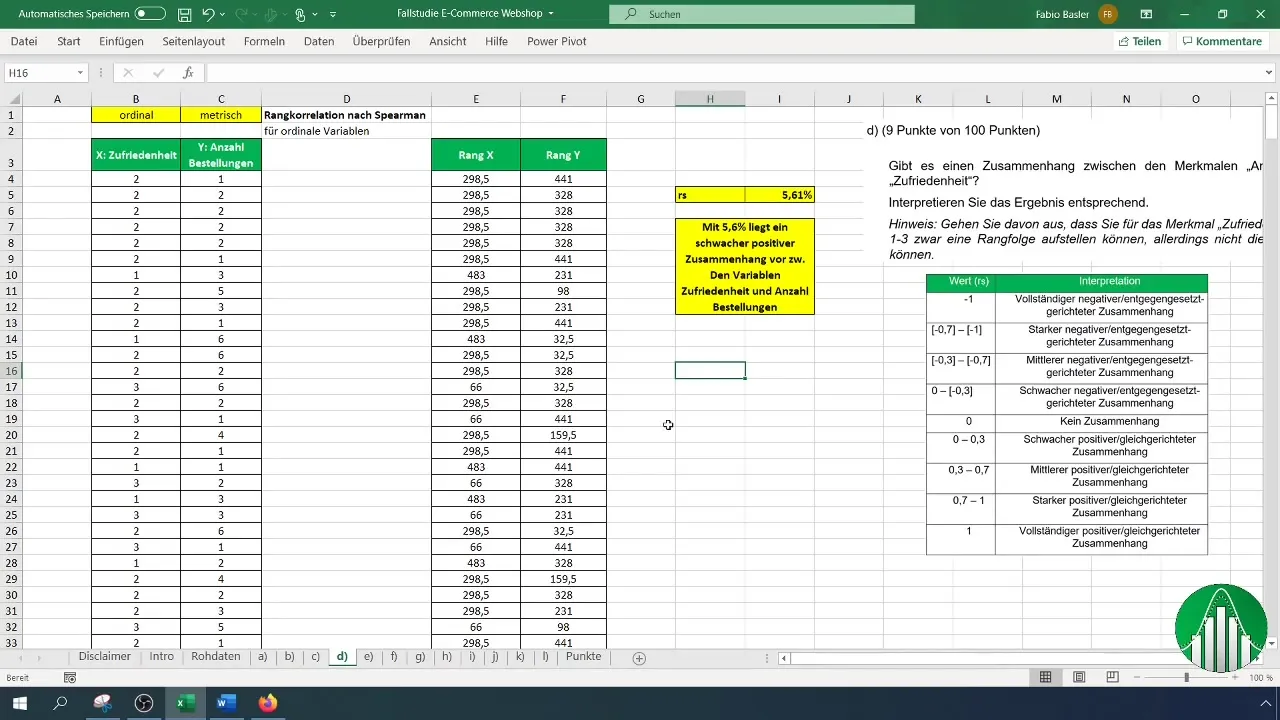
Aby zinterpretować wyniki, skorzystaj z tabeli wartości, która zawiera różne zakresy korelacji rangowej. Po interpretacji potwierdzamy, że niska wartość współczynnika korelacji oznacza, że zmienne są względnie niezależne.
Podsumowanie
Przeprowadzenie analizy korelacji rangowej D'Alemberta w Excelu pozwala uzyskać wartościowe spostrzeżenia na temat związków między zmiennymi porządkowymi i metrycznymi. Metoda ta jest łatwa w użyciu i zapewnia klarowne spojrzenie na ewentualne zależności.
Najczęściej zadawane pytania
Jaki jest współczynnik korelacji rang Spearmana?Współczynnik korelacji rang Spearmana mierzy siłę i kierunek monotonicznego związku między dwiema zmiennymi.
Kiedy warto używać współczynnika Spearmana?Warto go używać, gdy przynajmniej jedna zmienna jest skategoryzowana ustawnie.
Jak obliczyć współczynnik Spearmana w programie Excel?Skorzystaj z funkcji „Rang.Mittel”, aby uzyskać rangi, a następnie z funkcji „KORREL”, aby obliczyć związek.
Jaki jest zakres wartości dla współczynnika Spearmana?Współczynnik mieści się w zakresie od -1 do 1. Wartości zbliżone do 1 wskazują na silną dodatnią korelację, podczas gdy wartości zbliżone do -1 wskazują na silną ujemną korelację.
Co może oznaczać wartość 5,61% w korelacji rangowej?Wartość 5,61% wskazuje na słaby dodatni związek, co sugeruje, że zmienne są względnie niezależne.


