Obliczanie prawdopodobieństw w Excelu za pomocą rozkładu Poissona

Obliczenia statystyczne są niezbędną częścią analizy danych, zwłaszcza w środowisku e-commerce. Analiza danych historycznych umożliwia określenie prawdopodobieństw, które są kluczowe dla firm. W tym samouczku dowiesz się, jak obliczać prawdopodobieństwa przy użyciu rozkładu Poissona w Excelu na podstawie studium przypadku z ankiety.

Najważniejsze wnioski Rozkład Poissona umożliwia określenie prawdopodobieństwa zdarzeń, które występują w ustalonym ramie czasowym. W tym przykładzie obliczysz prawdopodobieństwo, że więcej niż dwa, ale nie więcej niż czterech klienci kupią coś w sklepie e-commerce w ciągu godziny, oraz prawdopodobieństwo, że więcej niż dwóch klienci ogółem coś kupią.

Krok po kroku

Rozpocznijmy obliczanie prawdopodobieństw dla opisanych zdarzeń.

Krok 1: Zrozumienie podstaw rozkładu Poissona

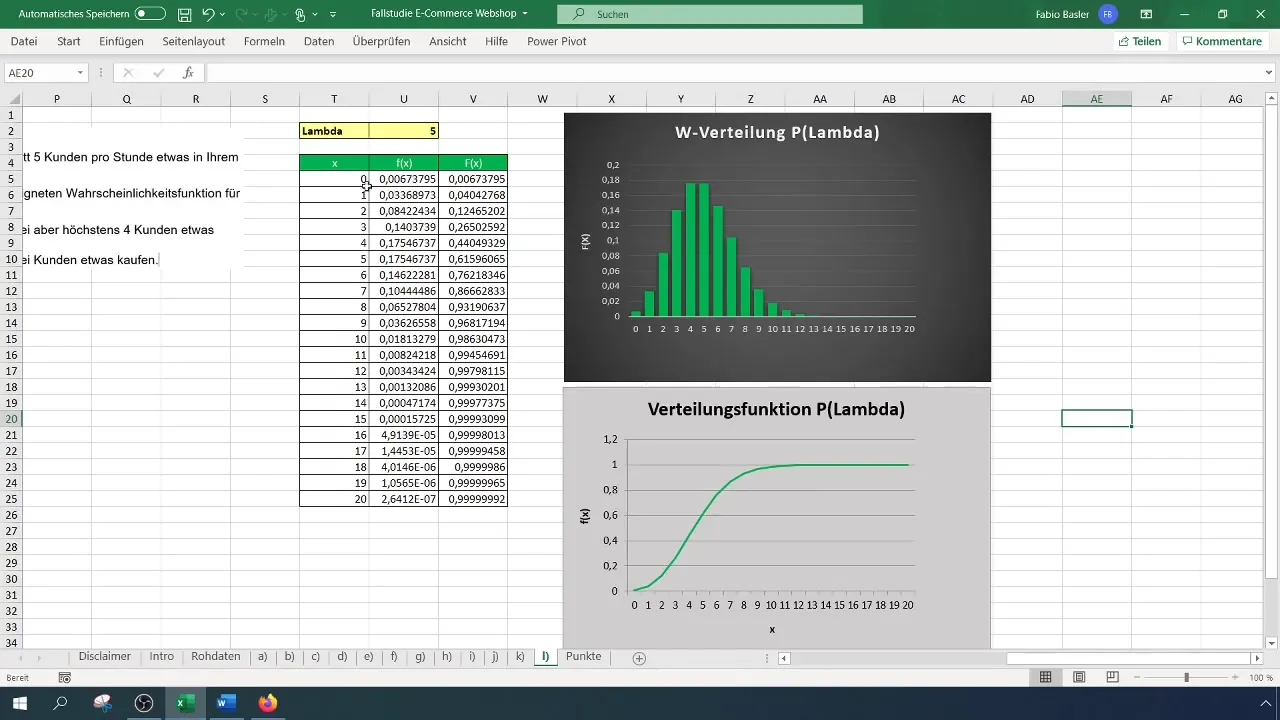
Najpierw ważne jest, abyś zrozumiał, czym jest rozkład Poissona. Ten dyskretny rozkład prawdopodobieństwa służy do kwantyfikowania liczby zdarzeń w ustalonych okresach czasu. W tym konkretnym przykładzie mamy średnią liczbę pięciu zakupów na godzinę. Formułujesz to jako wartość lambda (λ = 5).

Krok 2: Przygotowanie danych w Excelu

Otwórz Excel i przygotuj nową tabelę. Upewnij się, że wartości niezbędne parametry (Lambda i liczba pożądanych zdarzeń) są dobrze widoczne.

Krok 3: Określenie prawdopodobieństw zakupów przez klientów

W pierwszym scenariuszu chcesz obliczyć prawdopodobieństwo, że więcej niż dwoje, ale nie więcej niż czworo klienci kupią coś. Musisz obliczyć prawdopodobieństwa dla dwóch i czterech klientów, a następnie wyznaczyć różnicę między nimi.

Krok 4: Wykorzystanie formuły Excela dla rozkładu Poissona

Skorzystaj z funkcji POISSON.WAHRSCHEINLICHKEIT, aby obliczyć prawdopodobieństwa. Formuła wygląda następująco:

• Dla dwóch kupujących: =POISSON.WAHRSCHEINLICHKEIT(2; 5; WAHR).
• Dla czterech kupujących: =POISSON.WAHRSCHEINLICHKEIT(4; 5; WAHR).

Krok 5: Interpretacja wyników

Po zastosowaniu formuł otrzymasz dwa prawdopodobieństwa, na przykład 12% dla dwóch klientów i 44% dla czterech klientów. Następnie odejmujesz prawdopodobieństwo dla dwóch kupujących od czterech kupujących, co daje ci prawdopodobieństwo 32%, że więcej niż dwóch, ale nie więcej niż czterech klientów coś kupią.

Krok 6: Obliczanie dodatkowych prawdopodobieństw

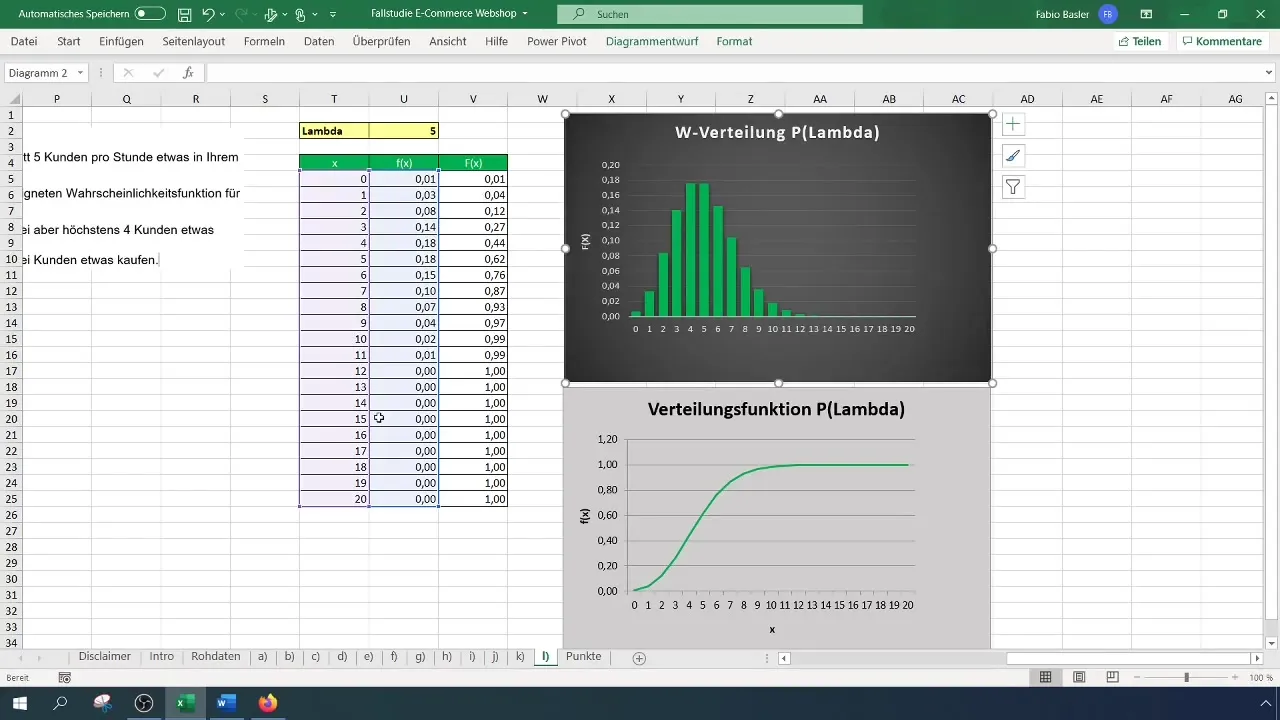
Teraz chodzi o obliczenie prawdopodobieństwa, że więcej niż dwaj klienci kupią coś w twoim sklepie e-commerce. Aby to zrobić, najpierw obliczasz prawdopodobieństwo dokładnie dwóch kupujących i odejmujesz ten wynik od 1.

Krok 7: Wykorzystanie formuły Excela dla więcej niż dwóch kupujących

Formuła w Excelu wygląda następująco: =1 - POISSON.WAHRSCHEINLICHKEIT(2; 5; WAHR). To daje ci prawdopodobieństwo, że więcej niż dwaj klienci coś kupią, wynoszące w tym przypadku 88%.

Krok 8: Podsumowanie wyników

Po przeprowadzeniu wszystkich obliczeń otrzymasz kluczowe prawdopodobieństwa. Znalazłeś, że prawdopodobieństwo, że więcej niż dwaj, ale nie więcej niż czterej klienci złożą zamówienie, wynosi 32%, podczas gdy prawdopodobieństwo, że więcej niż dwaj klienci ogółem coś kupią, wynosi 88%.

Podsumowanie

W tej instrukcji nauczysz się, jak wykorzystać rozkład Poissona do obliczania prawdopodobieństw w Excelu. Wykonasz kroki, aby obliczyć i interpretować prawdopodobieństwa dla konkretnych zdarzeń.