A análise de correlações é uma competência fundamental indispensável em muitos domínios científicos e empresariais. Utilizando o Excel, pode calcular o coeficiente de correlação de Pearson para medir quantitativamente as relações entre variáveis. Neste guia, vou mostrar-lhe passo a passo como efetuar uma análise de correlação para o comportamento de vendas de smartphones e computadores portáteis no Excel. Este processo não só ilustra a aplicação de conceitos estatísticos, como também mostra como é fácil utilizar o Excel para analisar dados.
Principais conclusões
- O coeficiente de correlação de Pearson fornece uma avaliação quantitativa da relação entre duas variáveis.
- Conheça os diferentes métodos para calcular o coeficiente de correlação no Excel.
- A visualização dos resultados através de gráficos facilita a compreensão das relações entre as variáveis.
Instruções passo a passo
O procedimento seguinte mostra-lhe como calcular o coeficiente de correlação de Pearson no Excel. Centramo-nos nas vendas de smartphones e computadores portáteis para demonstrar uma aplicação clara e prática.
Para iniciar a análise de correlação, comece por abrir um novo livro de trabalho do Excel ou utilize um já existente onde estejam disponíveis os dados relevantes.

Em primeiro lugar, deve certificar-se de que as vendas correspondentes de smartphones e computadores portáteis são introduzidas em duas colunas separadas. Estas colunas constituem a base de dados em que se baseia a análise. Certifique-se de que os dados são introduzidos completa e corretamente para evitar resultados distorcidos.
Uma vez introduzidos os dados, selecione as duas colunas com as vendas. Para calcular o coeficiente de correlação, introduza a fórmula =CORREL() numa célula vazia, seguida dos dois intervalos de dados. Esta função calcula o coeficiente de correlação de Pearson com base nos dados selecionados.
Se aplicar a fórmula =CORREL(intervalo1; intervalo2), selecione todo o intervalo da coluna que representa as vendas de computadores portáteis, seguido do intervalo de vendas de smartphones. O resultado fornecerá o valor da correlação entre essas variáveis. Se a correlação for elevada, cerca de 0,96, isso indica uma forte relação positiva.
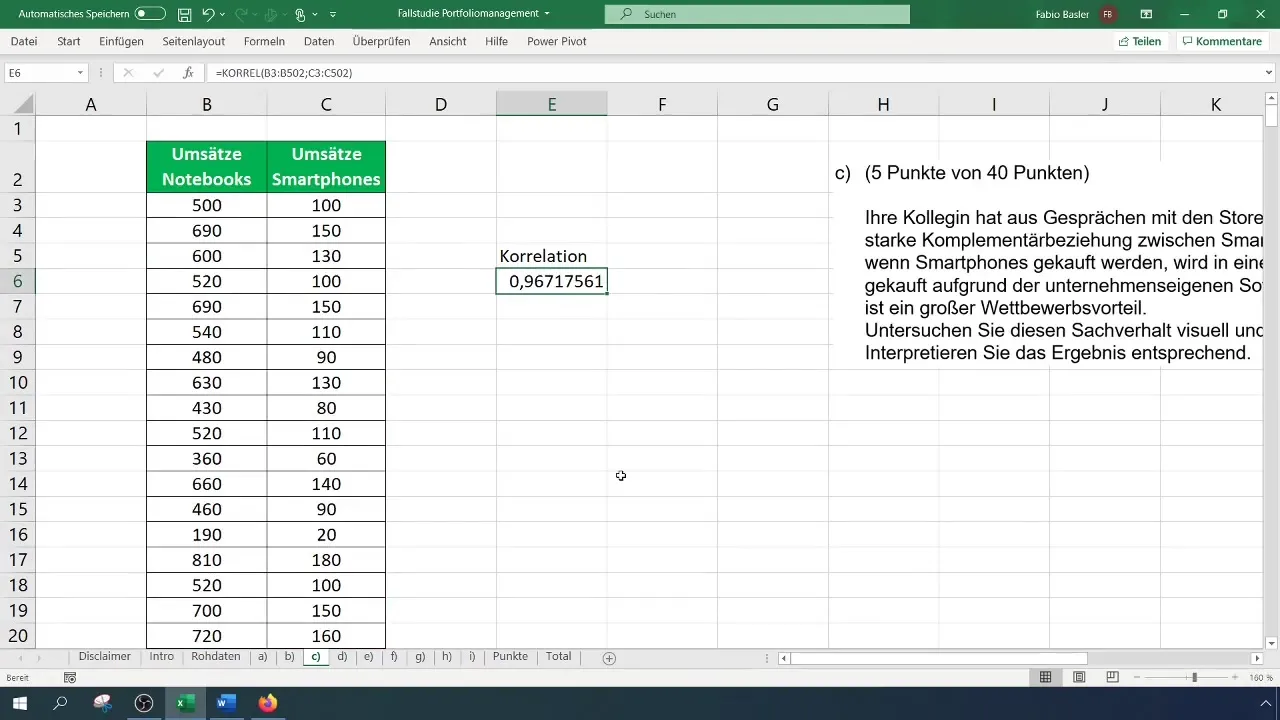
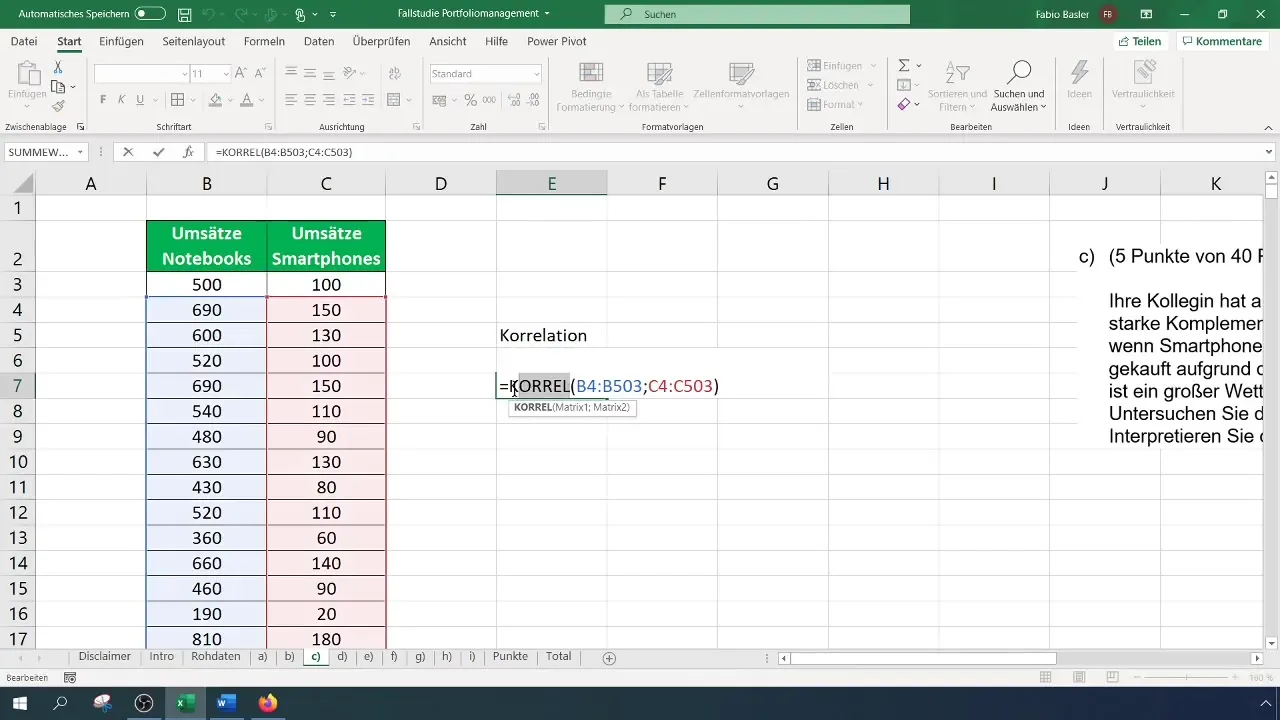
Para além da função KORREL, também pode utilizar a função =PEARSON(), que dá um resultado idêntico. Introduza esta função de forma semelhante à anterior e selecione os intervalos de dados para determinar a correlação.
Outra opção interessante para analisar correlações é a função de análise de dados no Excel. Para ativar esta função, vá ao menu "Ficheiro" e depois a "Opções". Em "Suplementos", pode ativar a opção de análise de dados, se ainda não estiver activada.
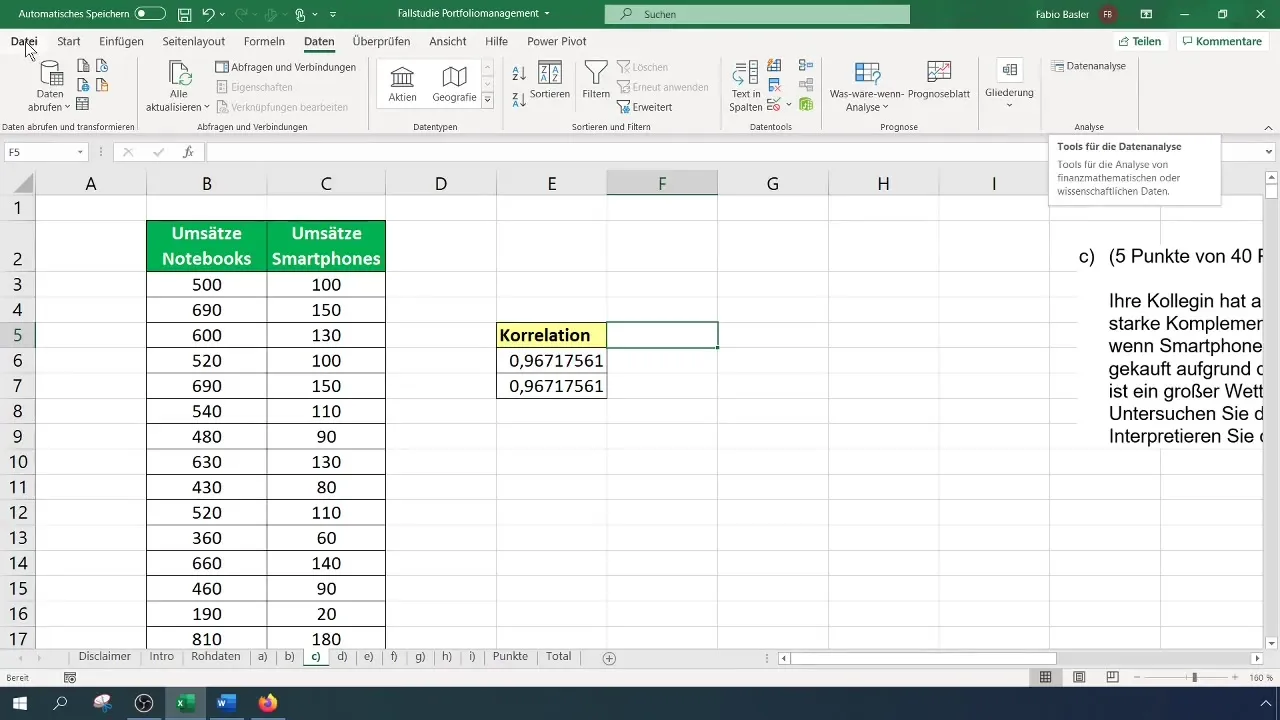
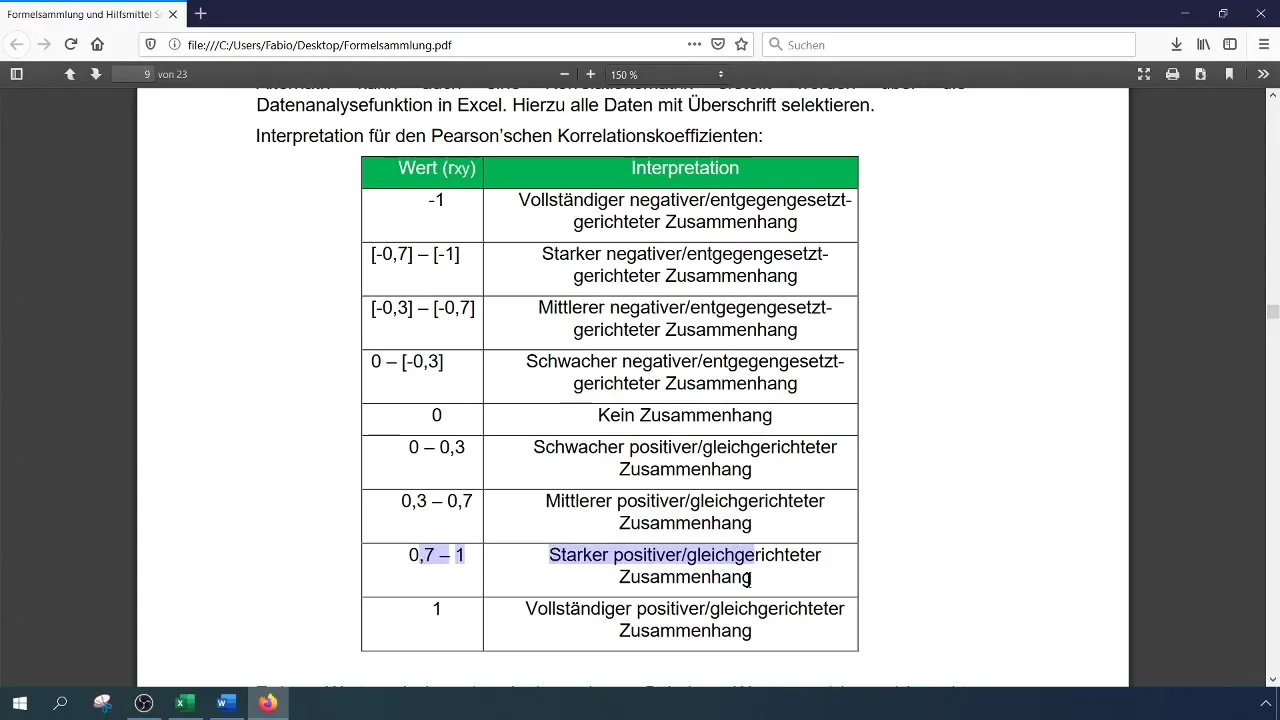
Depois de ativar a função de análise de dados, selecione "Análise de dados" no friso e clique em "Correlação". Abre-se um ecrã de entrada no qual define a área de entrada para os dados, incluindo os títulos das colunas.
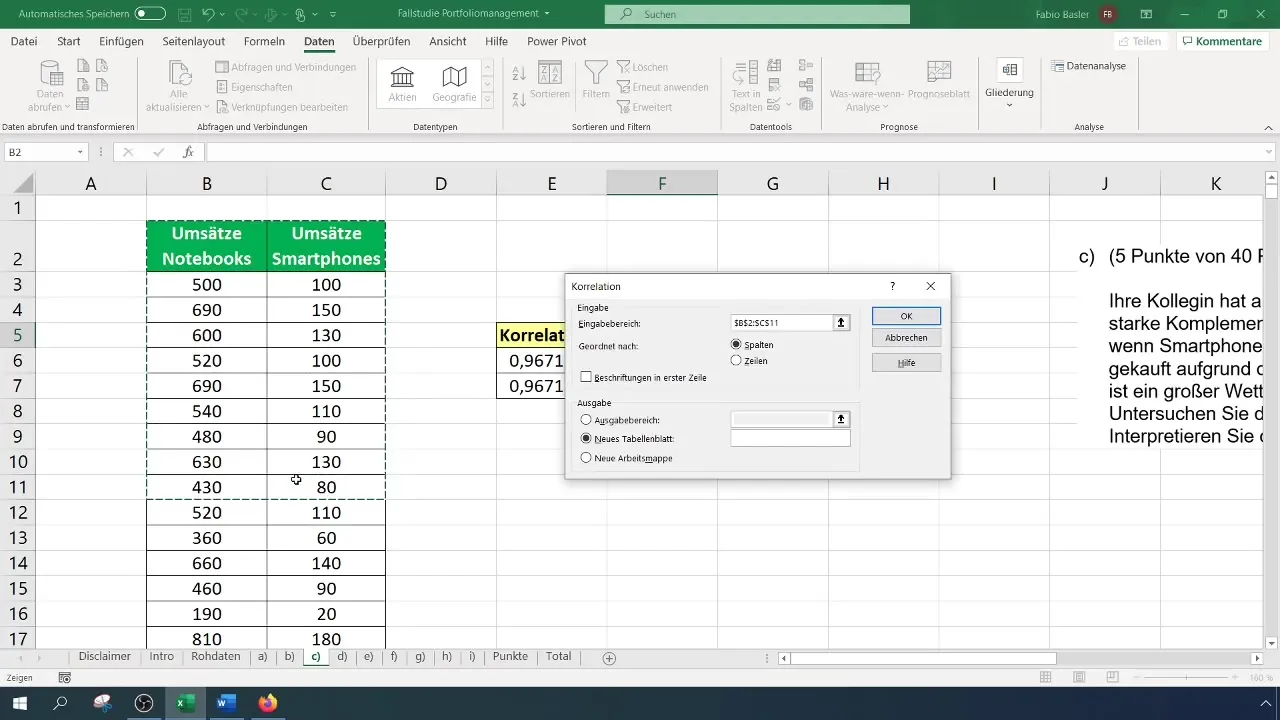
Ao definir o intervalo de saída, deve selecionar uma célula vazia na qual os resultados serão apresentados. Ao confirmar a entrada, é gerada uma matriz de correlação que mostra todas as relações dentro dos dados especificados. Aqui, nota-se novamente a alta correlação de cerca de 0,96.
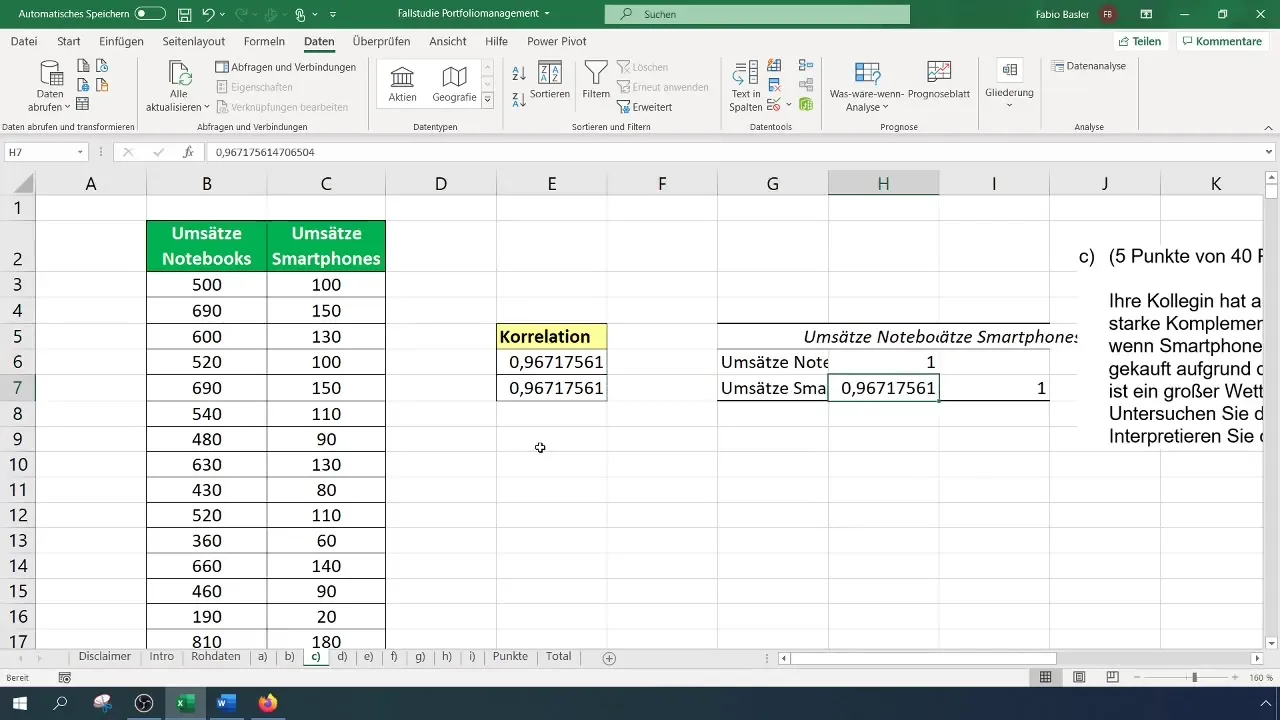
Um gráfico de dispersão é adequado para visualizar a relação entre as variáveis. Para tal, selecione uma célula vazia e insira um diagrama XY. Clique com o botão direito do rato no gráfico e selecione "Selecionar dados".
Adicione as vendas de smartphones e computadores portáteis. Esta representação visual mostra como os pontos estão distribuídos entre as duas variáveis e ilustra a relação através dos efeitos de agrupamento.
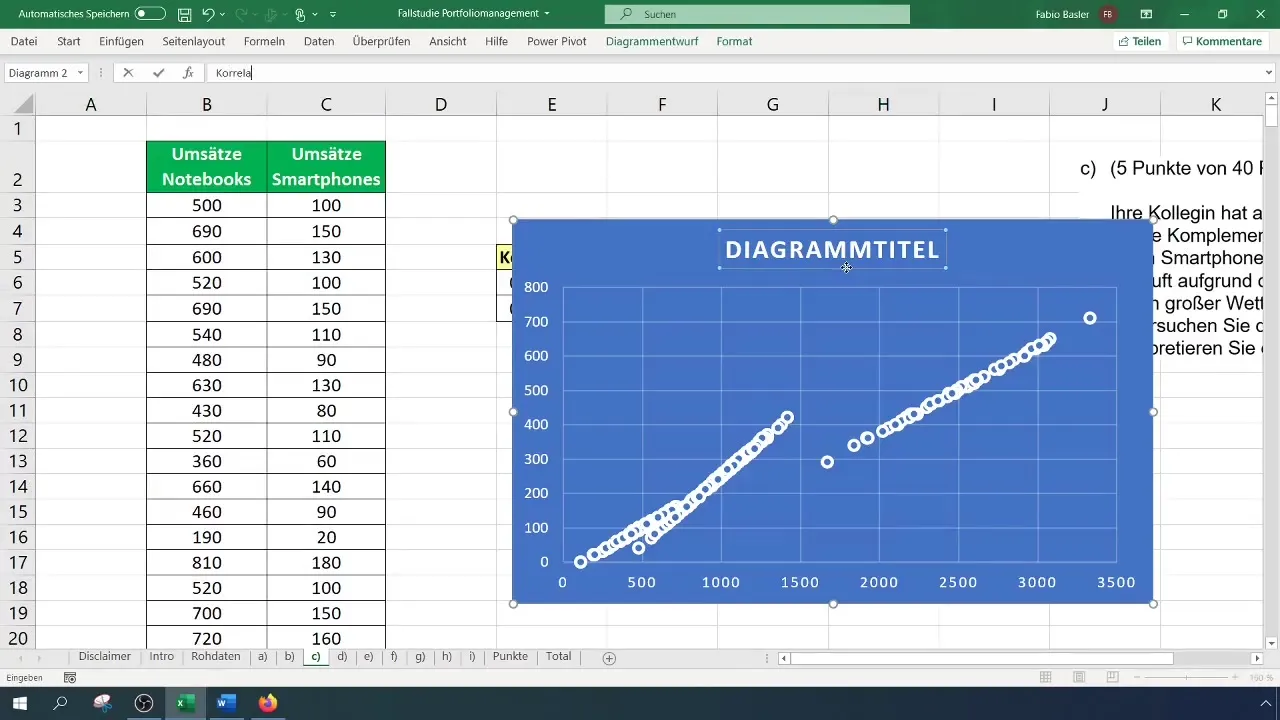
Uma forma adicional de analisar a relação é adicionar uma linha de tendência ao gráfico. Clique no sinal de mais no canto superior direito do gráfico e active a opção de linha de tendência. Também pode mostrar a fórmula e o coeficiente de determinação R² para uma análise mais aprofundada.
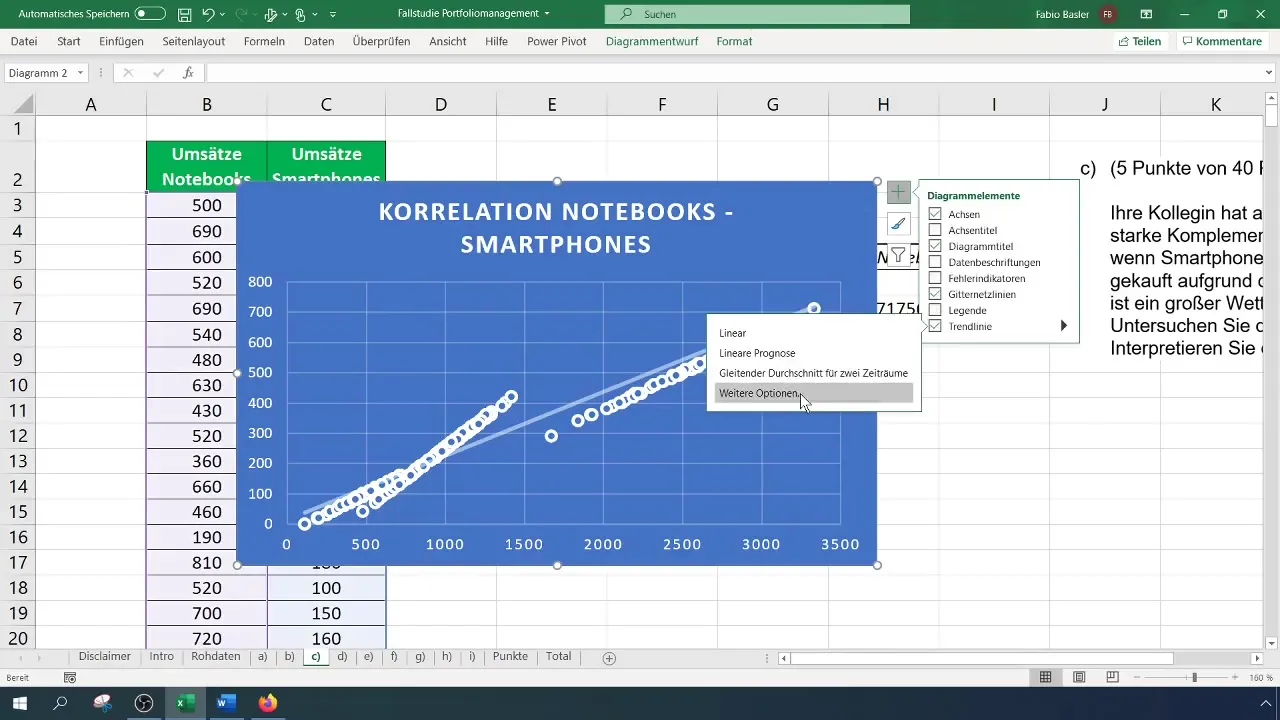
O coeficiente de determinação indica quão bem a linha de tendência descreve os dados e é o valor ao quadrado do coeficiente de correlação. Um R² de aproximadamente 0,935 reforça a força da relação entre os computadores portáteis e os smartphones, o que apoia a correlação calculada anteriormente.
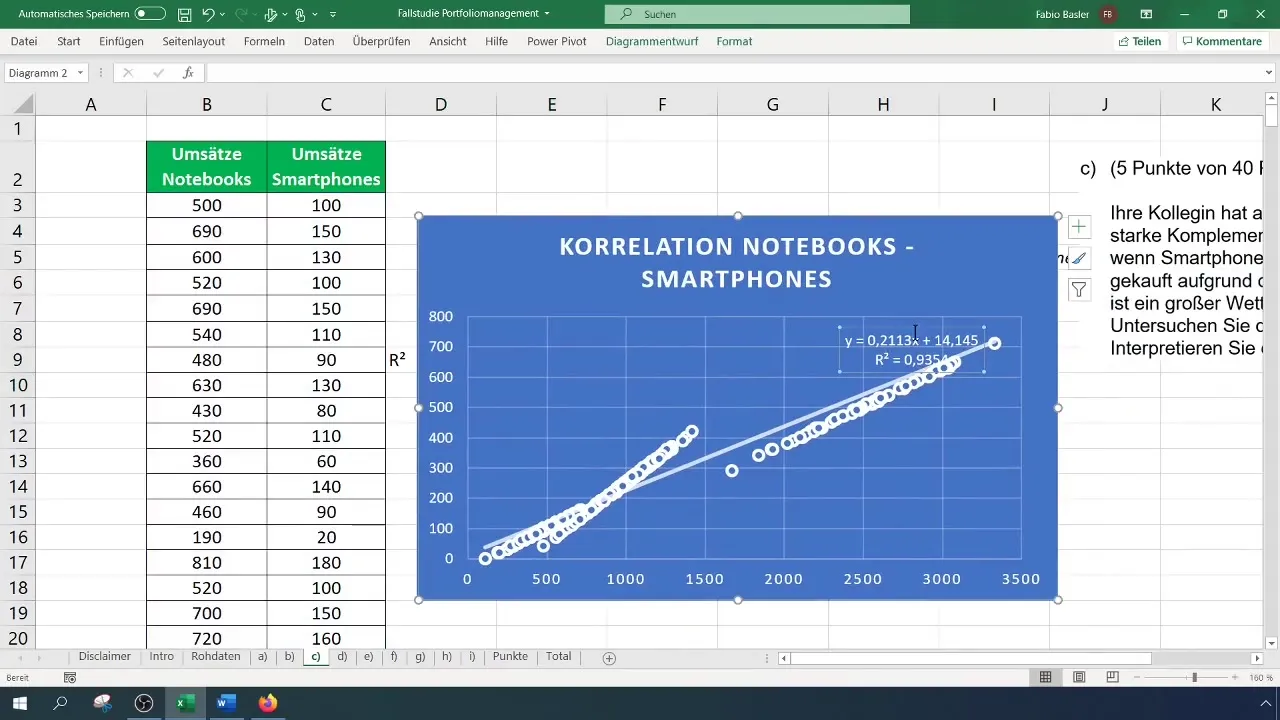
Por fim, é importante interpretar os resultados. Valores acima de 0,90 indicam uma forte correlação positiva, o que significa que um aumento numa área de vendas é acompanhado por um aumento na outra. Neste caso, a relação entre as vendas de smartphones e portáteis é extremamente forte.
Resumo
Neste guia, aprendeu a calcular e a interpretar o coeficiente de correlação de Pearson no Excel. Os vários métodos mostraram-lhe várias formas de visualizar quantitativa e visualmente a correlação entre as variáveis. Isto dá-lhe a oportunidade de analisar dados reais e obter informações comerciais importantes.
Perguntas mais frequentes
Como posso calcular o coeficiente de correlação de Pearson no Excel?Pode utilizar a função =CORREL(intervalo1; intervalo2) para calcular o coeficiente de correlação de Pearson.
O que é que um valor de correlação de 0,96 indica?Um valor de correlação de 0,96 indica uma forte relação positiva entre as variáveis analisadas.
Como posso ativar a função de análise de dados no Excel?Vá a "Ficheiro" > "Opções" > "Suplementos", selecione "Suplementos do Excel" e assinale a caixa "Função de análise".
Também posso calcular o coeficiente de correlação com uma matriz?Sim, pode utilizar a função "Análise de dados" para criar uma matriz de correlação para várias séries de dados.
Como interpreto o coeficiente de determinação R²? Um valor R² próximo de 1 indica que uma proporção elevada da variância na variável dependente é explicada pela variável independente.


