Os testes estatísticos são uma componente central da análise de dados e da tomada de decisões. Especialmente no domínio da biotecnologia, pode ser crucial testar hipóteses sobre a taxa de sucesso de substâncias activas. Neste tutorial, aprenderá a efetuar eficientemente um teste de uma amostra (teste 1-SP ) para o valor esperado com variância conhecida no Excel.
Principais conclusões
Este guia ensina-lhe:
- A base teórica do teste 1-SP.
- Os passos para efetuar o teste no Excel.
- A interpretação dos resultados.
Preparação dos dados
Para efetuar o teste 1-SP em Excel, é necessário dispor dos dados relevantes. No nosso exemplo, assumimos uma situação em que se está a analisar a taxa de sucesso de ingredientes activos. Sabe-se que a taxa média de sucesso era de 59%, com um desvio padrão de 19. Em primeiro lugar, deve introduzir os seus dados numa folha de cálculo do Excel.
Certifique-se de que os seus dados estão organizados em colunas para poder aceder-lhes mais tarde. Uma visão geral clara ajudá-lo-á a compreender mais facilmente as etapas individuais.
Resumo do teste
O teste 1-SP é utilizado para verificar se o valor médio de sucesso difere significativamente de um valor especificado. Neste caso, verificamos se a taxa de sucesso de 59% pode ser significativamente aumentada no futuro.
Formular hipóteses
As hipóteses que formula para o teste são cruciais:
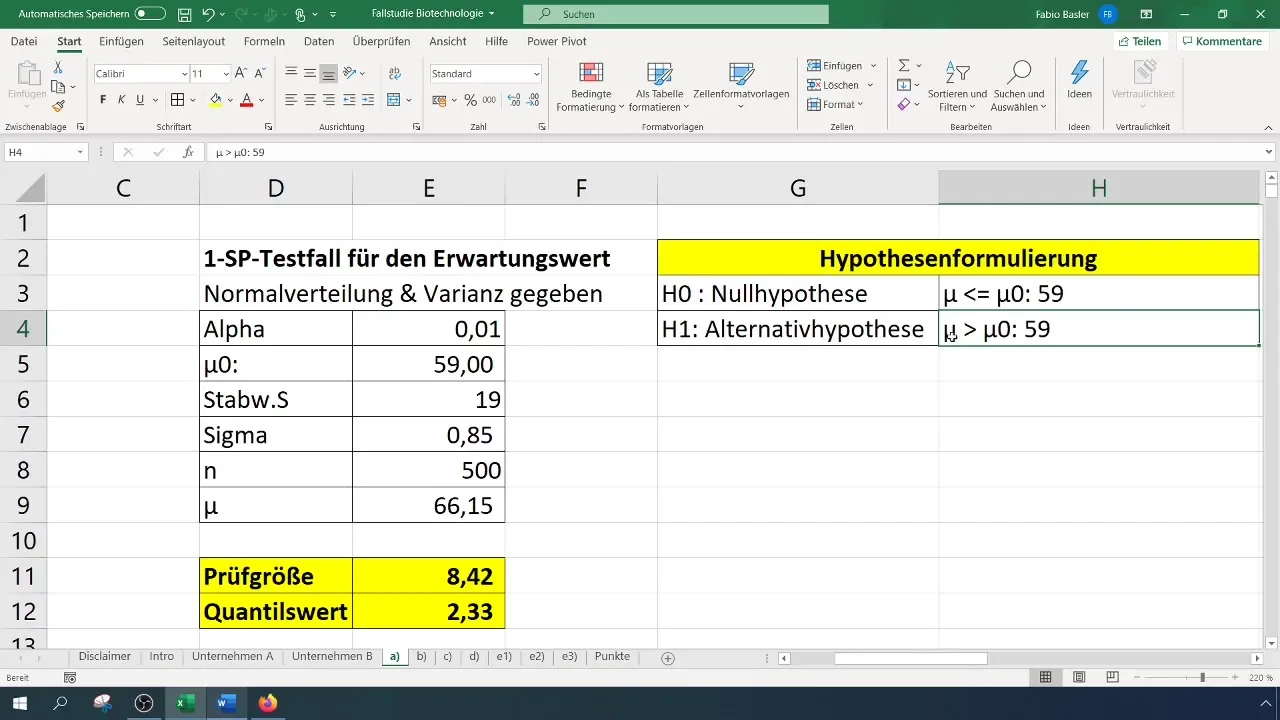
- Hipótese nula (H0): O verdadeiro valor esperado é igual a 59 (σ = 59%).
- Hipótese alternativa (H1): O verdadeiro valor esperado é maior que 59%.
Ao formular as hipóteses, a atenção deve centrar-se no que é exatamente necessário testar e na forma como isso se apresenta no seu contexto.
É importante reconhecer claramente a diferença entre a hipótese nula e a hipótese alternativa, uma vez que estas constituem a base para os cálculos seguintes.
Recolha da amostra
Para o nosso teste, recolhemos uma amostra de 500 ingredientes activos. É importante notar que a seleção da amostra é representativa e deve garantir, através do método adequado, que os resultados podem ser transferidos de forma realista para a população em geral.
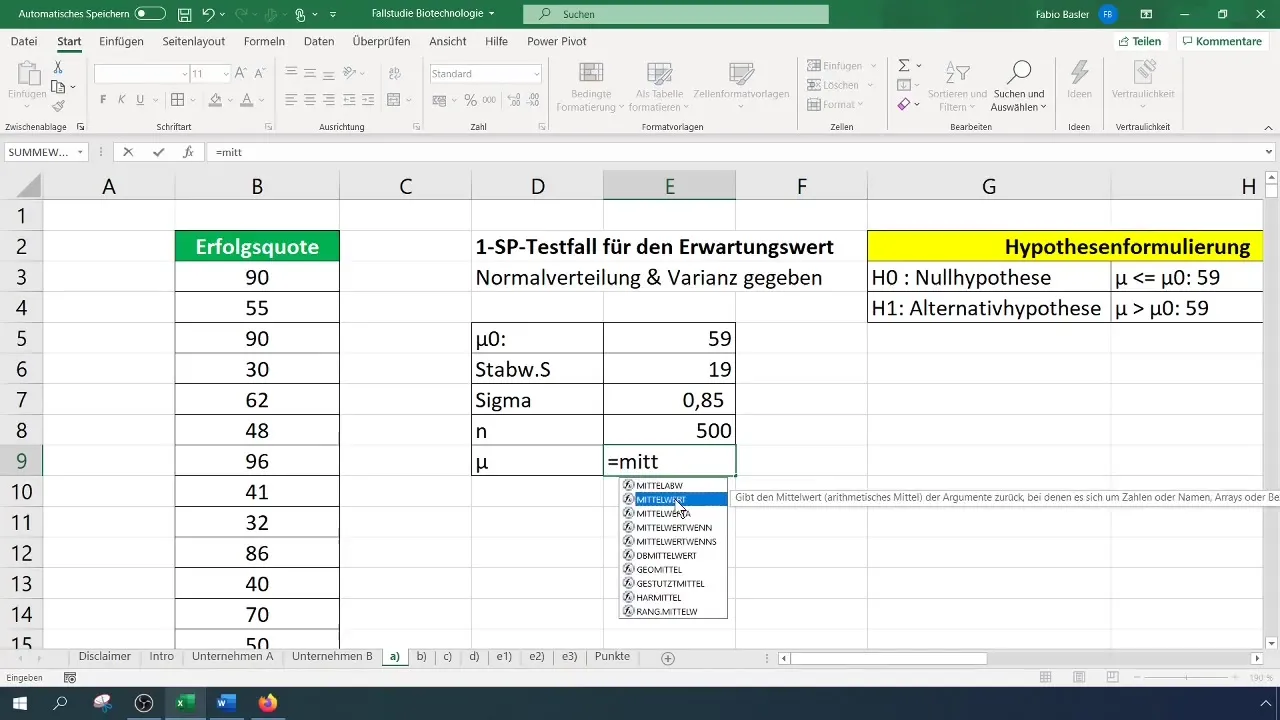
Para o teste, começa-se por calcular a média aritmética. Isto deve ser fácil de fazer, utilizando a fórmula adequada no Excel.
Cálculo da variável de teste
A variável de teste para um teste 1-SP é determinada pela seguinte fórmula
[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]
Aqui (\bar{x}) representa o valor médio da sua amostra, (\mu_0) representa o valor médio assumido (neste caso 59), (\sigma) representa o desvio padrão (aqui 19) e (n) representa o número de amostras (500).
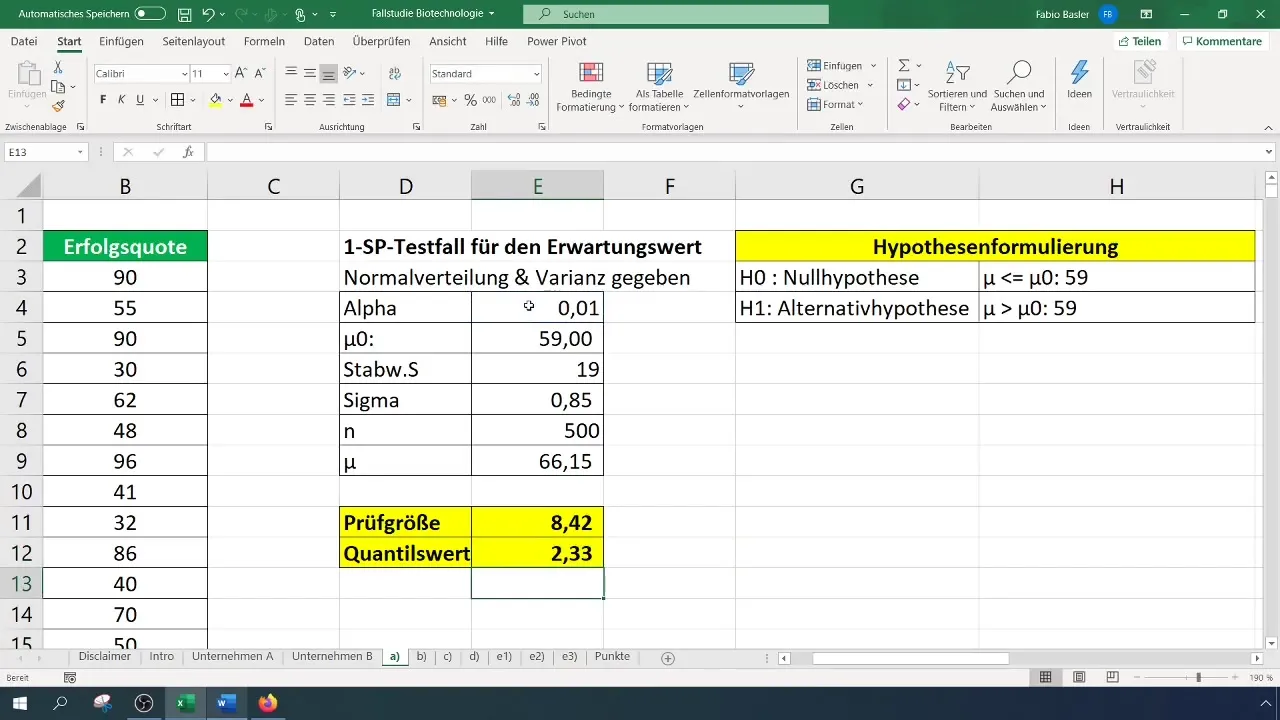
Depois de inserir os valores na fórmula, calcule o teste estatístico para determinar se é significativo ou não.
Determinação do valor crítico
Para um nível de significância de 1% (0,01), é necessário ler ou calcular o valor crítico. Isto pode ser feito no Excel com a função NORM.S.INV.
A fórmula é:
[ \text{NORM.S.INV}(1 - \alpha) ]
Em que (\alpha) é o nível de significância (0,01). O valor determinado é utilizado como base de comparação com a variável de teste.
Realização do teste
Agora que tem a estatística de teste e o valor crítico, compare os dois:
- Se a estatística de teste for maior do que o valor crítico, a hipótese nula é rejeitada.
- Caso contrário, não é possível rejeitar a hipótese nula.
No nosso caso, isso resulta em uma estatística de teste de 8,4, que excede o valor crítico de 2,33. Portanto, podemos rejeitar a hipótese nula. Isto indica que a taxa de sucesso foi significativamente melhorada.
Interpretação dos resultados
Uma vez efectuado o teste e obtidos os resultados, é necessário interpretá-los num contexto claro. Rejeitar a hipótese nula significa que o novo valor testado é significativamente diferente do anterior, neste caso, 59%.
Esta informação é extremamente importante para a tomada de decisões estratégicas na sua organização. Confirma que os esforços para melhorar a taxa de sucesso foram eficazes.
Resumo
Neste tutorial, aprendeu a efetuar um teste 1-SP para o valor esperado no Excel. Utilizando um estudo de caso, pôde seguir os passos desde a definição de hipóteses até ao cálculo dos dados e à interpretação dos resultados. Este conhecimento não é apenas valioso para análises científicas, mas também para aplicações práticas na empresa.


