O teste de qualidade de ajuste do qui-quadrado é um método simples para testar a hipótese de que uma determinada série de dados segue uma distribuição normal. Neste guia, você aprenderá como executar o teste qui-quadrado no Excel para determinar se as vendas de smartphones seguem uma distribuição normal. Iremos percorrer o processo passo a passo, desde a criação de uma tabela de frequência classificada até ao cálculo da estatística de teste e à sua comparação com o valor crítico do qui-quadrado.
Principais conclusões
- O teste de adequação do qui-quadrado ajuda a testar distribuições normais.
- É importante criar uma tabela de frequências classificadas.
- A estatística do teste é comparada com um valor crítico para rejeitar ou aceitar a hipótese nula.
Instruções passo a passo
Passo 1: Preparar os dados
Para efetuar o teste do qui-quadrado, precisa primeiro dos dados. Copie as vendas de smartphones para uma folha de cálculo do Excel. Certifique-se de que os dados estão organizados numa única coluna.

Passo 2: Criar um histograma
Para obter uma indicação visual inicial da distribuição, crie um histograma dos seus dados. Para o fazer, vá a "Inserir" e selecione "Gráficos". Adicione um histograma selecionando o intervalo para os dados.
Passo 3: Criar uma tabela de frequências classificadas
Precisa de uma tabela de frequências classificadas para o teste do qui-quadrado. Primeiro, determine o número de classes para a sua tabela - neste caso, utilizaremos seis classes. Calcule a largura dos intervalos e crie a tabela em conformidade.
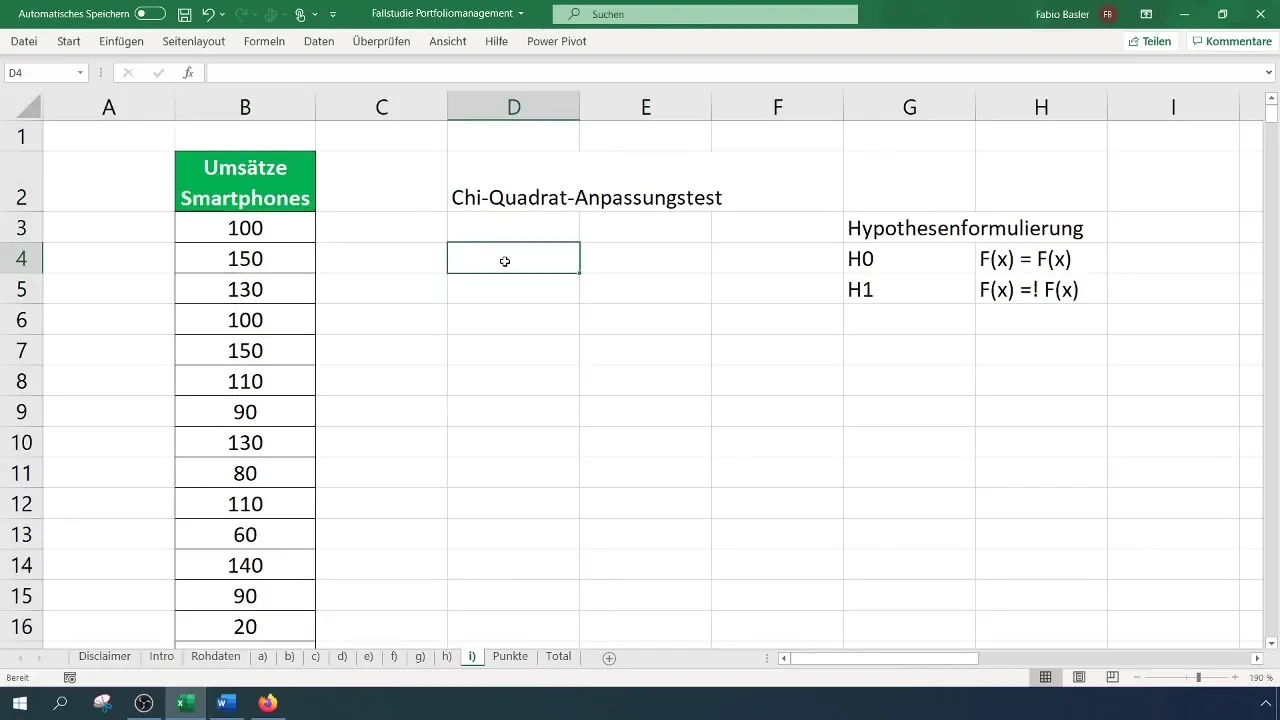
Passo 4: Calcular as frequências
Agora precisa de calcular as frequências observadas para cada classe. Vá a "Análise de dados" no menu e selecione "Histograma". Selecione o intervalo de entrada para os seus dados e os limites das classes. Determine o intervalo de saída para a tabela de frequências.
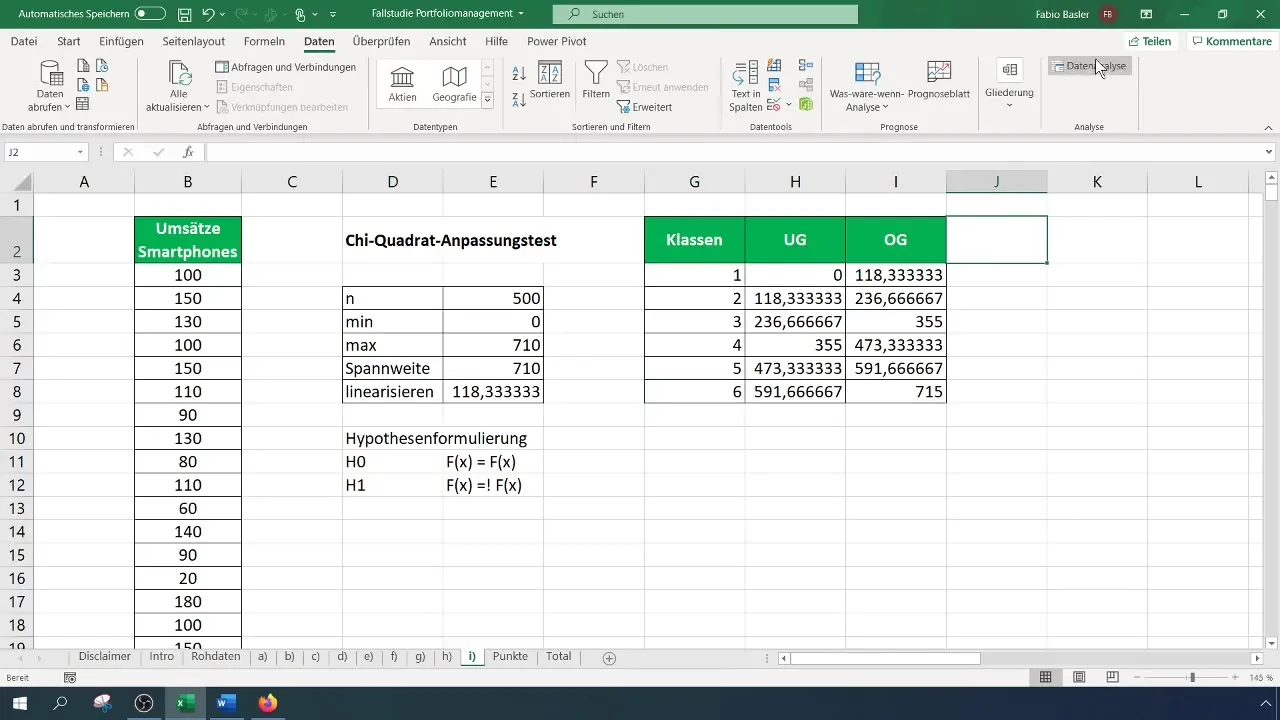
Passo 5: Calcular as frequências esperadas
Para determinar as frequências esperadas, calcule as probabilidades para cada classe com base na distribuição normal assumida. Para tal, necessita da média e do desvio padrão dos seus dados.
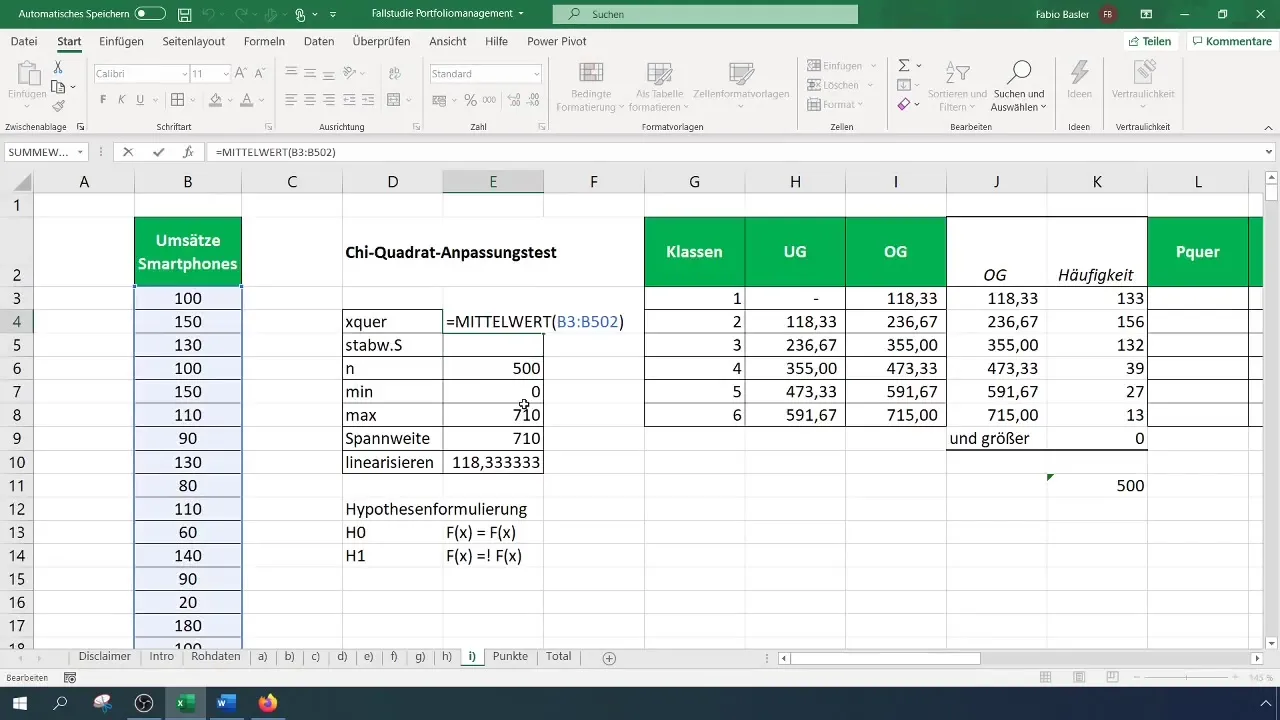
Passo 6: Calcular a estatística de teste
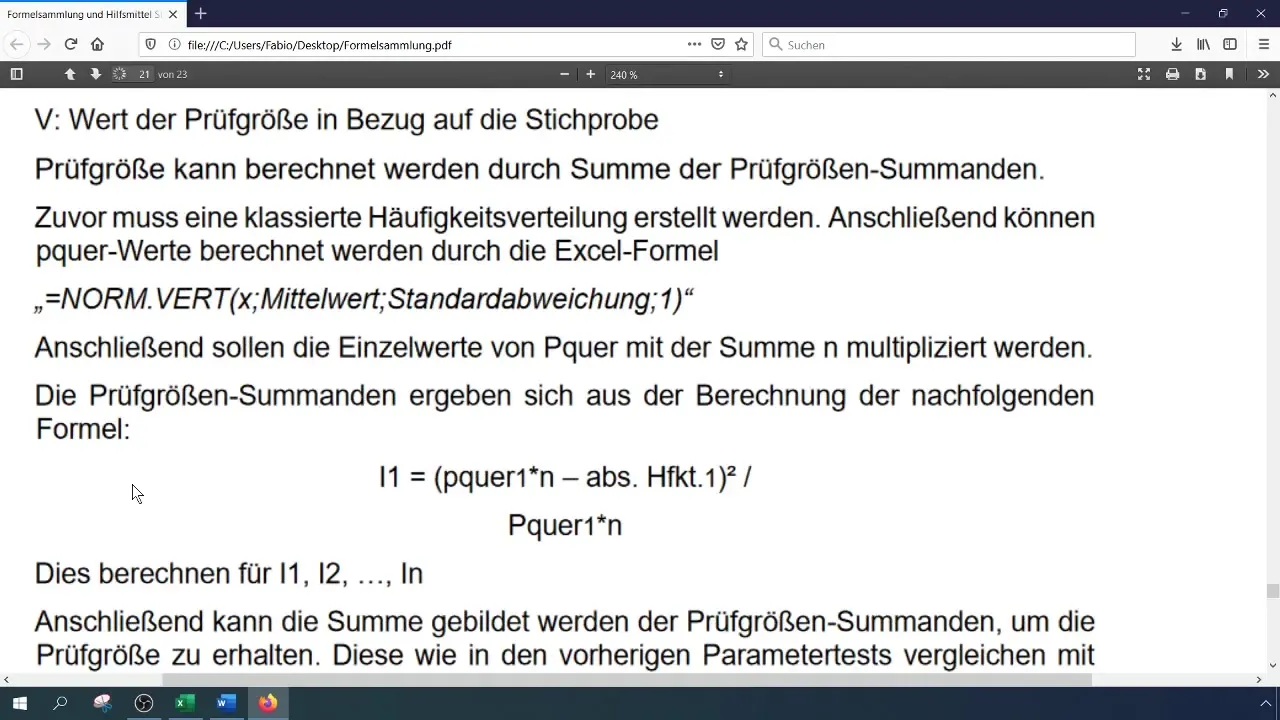
Calcule a estatística de teste (qui-quadrado) utilizando a fórmula
[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]
em que (O_i) são as frequências observadas e (E_i) as frequências esperadas. Pode efetuar este cálculo no Excel, guardando os componentes individuais em células separadas.
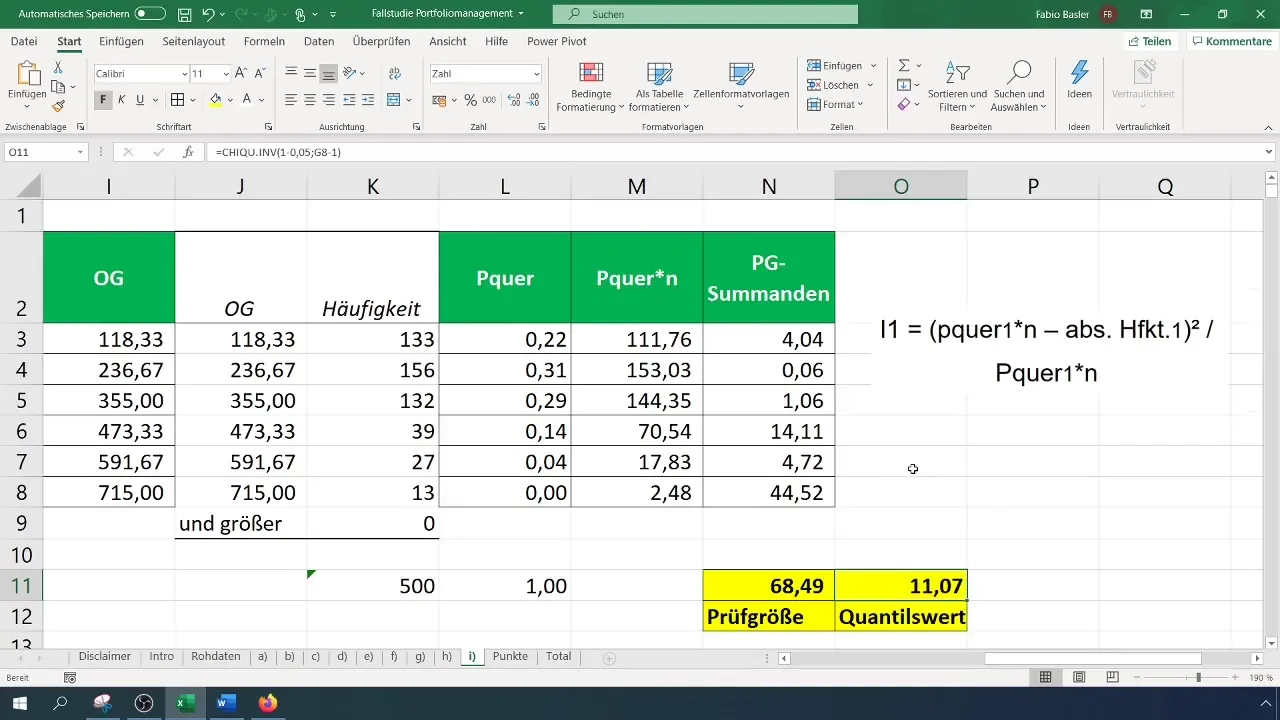
Passo 7: Calcular o valor crítico
Para avaliar o teste estatístico, é necessário calcular o valor crítico ( \chi^2 ) para o seu nível de confiança e o número de graus de liberdade. O número de graus de liberdade para o teste do qui-quadrado é (k - 1), em que (k) é o número de classes.
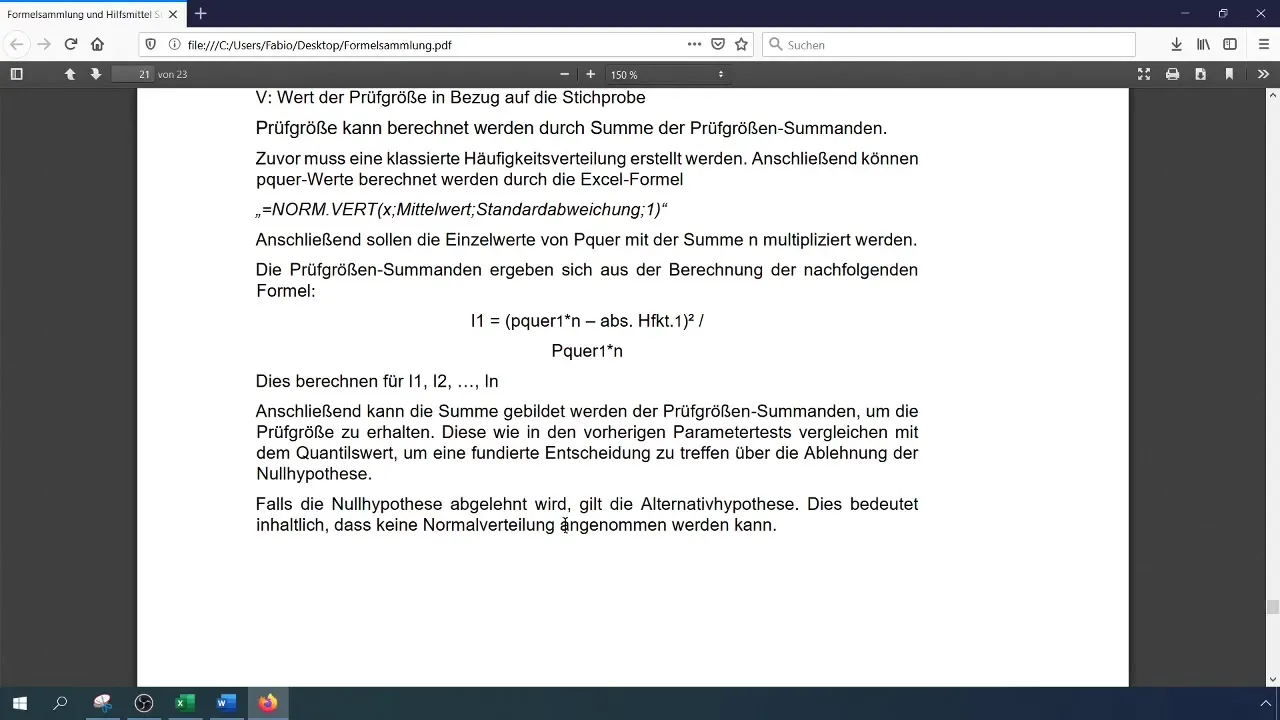
Passo 8: Teste as hipóteses
Compare a estatística de teste calculada com o valor crítico. Se a estatística de teste for maior do que o valor crítico, rejeite a hipótese nula, o que significa que os dados não são normalmente distribuídos. Caso contrário, aceite a hipótese nula.
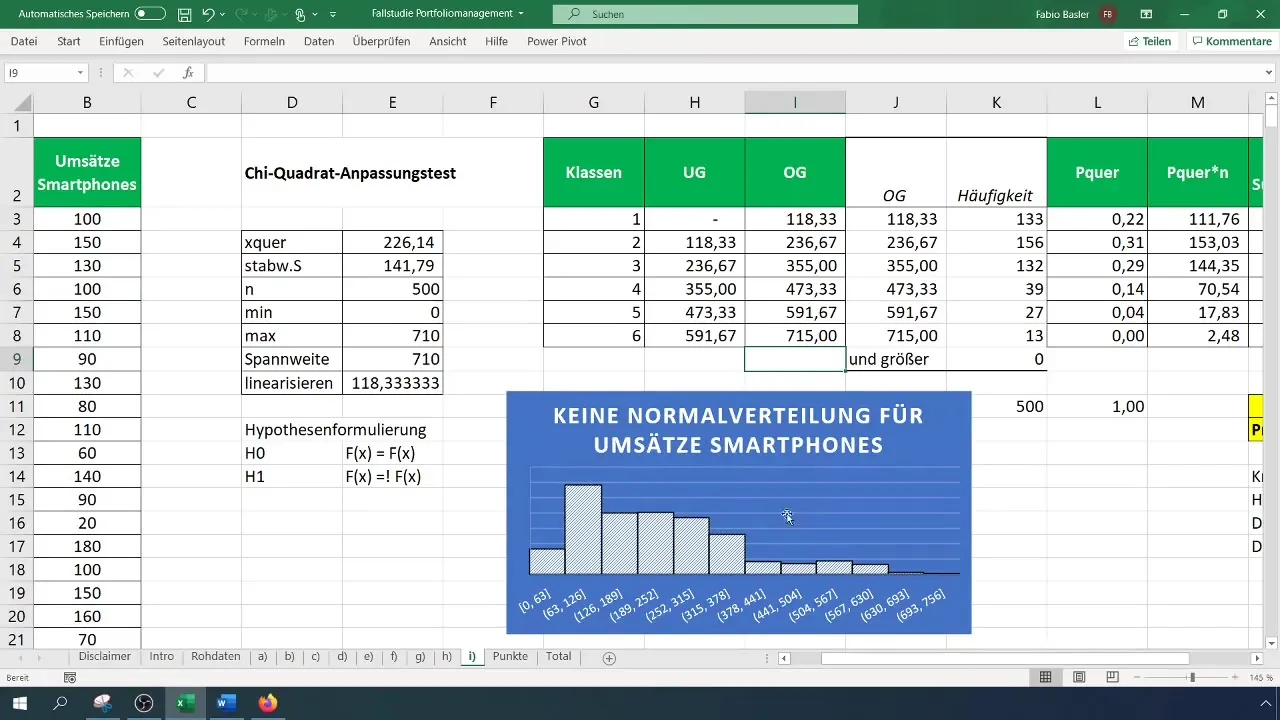
Passo 9: Resumir os resultados
Registe os seus resultados e expanda-os para incluir os dados gráficos e os testes de hipóteses. Não se esqueça de verificar o histograma para confirmar visualmente que a distribuição não é normal.
Resumir
Ao longo deste guia, aprendeu a efetuar o teste de ajuste Qui-Quadrado no Excel para analisar a distribuição normal das vendas do seu smartphone. As etapas incluem a criação de uma tabela de frequência classificada, cálculos para as frequências esperadas, a estatística de teste e, finalmente, a comparação com o valor crítico.


