Os cálculos estatísticos são uma parte indispensável da análise de dados, especialmente num ambiente de comércio eletrónico. A análise de dados históricos permite determinar probabilidades que são cruciais para as empresas. Neste guia, aprenderá a calcular probabilidades utilizando a distribuição de Poisson no Excel, com base num estudo de caso de um inquérito.
Principais lições A distribuição de Poisson permite determinar a probabilidade de eventos que ocorrem num período de tempo fixo. Neste exemplo, calcula-se a probabilidade de mais de dois, mas não mais de quatro clientes, comprarem algo numa loja de comércio eletrónico no espaço de uma hora, bem como a probabilidade de mais de dois clientes comprarem algo no total.
Instruções passo a passo
Vamos começar por calcular as probabilidades dos eventos descritos.
Passo 1: Compreender os princípios básicos da distribuição de Poisson
Antes de mais, é importante que compreenda o que é a distribuição de Poisson. Esta distribuição de probabilidade discreta é utilizada para quantificar o número de acontecimentos em períodos de tempo fixos. No exemplo atual, temos um valor médio de cinco compras por hora. Isto é formulado como um valor lambda (λ = 5).

Passo 2: Preparar os dados no Excel
Abra o Excel e prepare uma nova tabela. Certifique-se de que tem os parâmetros relevantes (lambda e o número de eventos desejados) claramente visíveis.
Passo 3: Determinar as probabilidades de compras dos clientes
Para o primeiro cenário, pretende calcular a probabilidade de mais de dois e, no máximo, quatro clientes comprarem algo. Para tal, é necessário calcular as probabilidades para dois e quatro clientes e, em seguida, determinar a diferença entre elas.

Passo 4: Utilizar a fórmula Excel para a distribuição de Poisson
Utilize a função POISSON.PROBABILITY para calcular as probabilidades. A fórmula é a seguinte:
- Para dois compradores: =POISSON.PROBABILITY(2; 5; TRUE).
- Para quatro compradores: =POISSON.PROBABILITY(4; 5; TRUE).
Etapa 5: Interpretar os resultados
Depois de aplicar as fórmulas, obtém duas probabilidades, por exemplo, 12% para dois clientes e 44% para quatro clientes. Agora subtraia a probabilidade de dois compradores da probabilidade de quatro compradores, o que lhe dá uma probabilidade de 32% de que mais de dois mas não mais de quatro clientes comprem algo.
Passo 6: Calcular outras probabilidades
Agora é altura de calcular a probabilidade de mais de dois clientes comprarem na sua loja de comércio eletrónico. Para tal, comece por calcular a probabilidade de haver exatamente dois compradores e subtraia este resultado a 1.
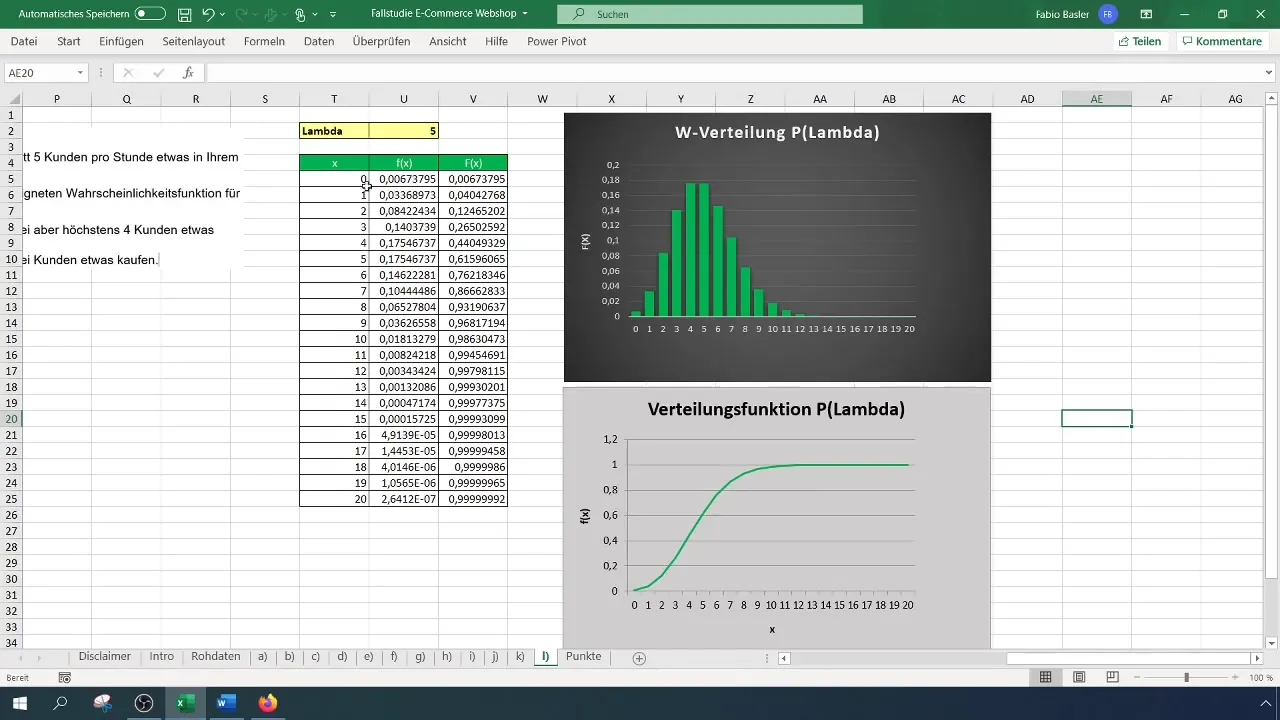
Passo 7: Utilizar a fórmula Excel para mais de dois compradores
A fórmula do Excel é: =1 - POISSON.PROBABILITY(2; 5; TRUE). Isto dá-lhe a probabilidade de mais de dois clientes comprarem algo, que neste caso é 88%.
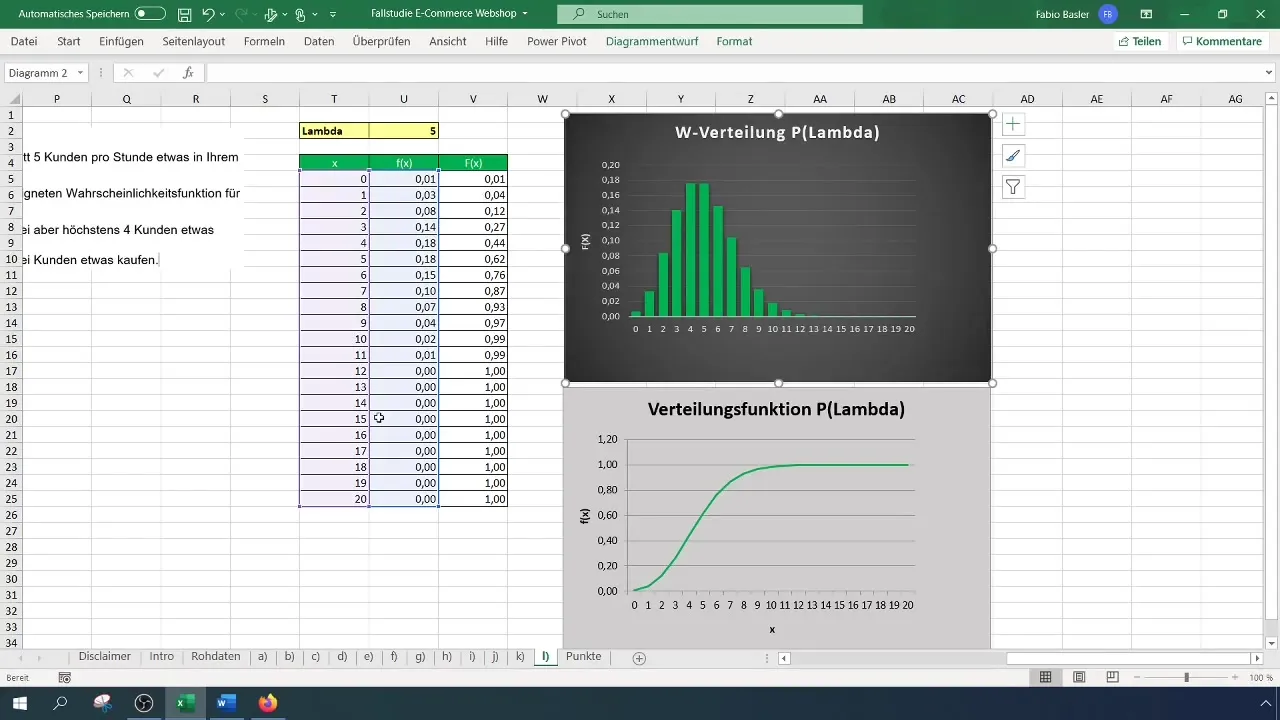
Passo 8: Resumir os resultados
Depois de efetuar todos os cálculos, anote as principais probabilidades. Descobriu que a probabilidade de mais de dois mas não mais de quatro clientes efectuarem encomendas é de 32%, enquanto a probabilidade de mais de dois clientes comprarem no total é de 88%.
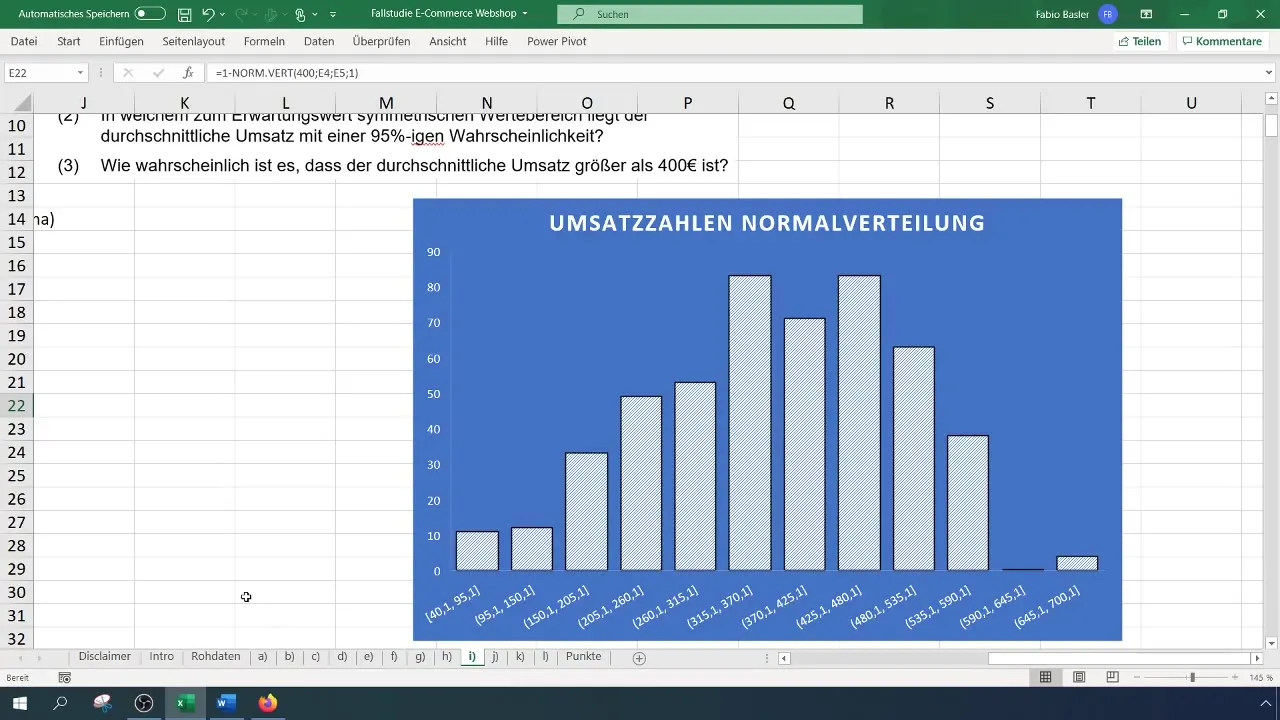
Resumo
Neste tutorial, você aprendeu a usar a distribuição de Poisson para calcular probabilidades no Excel. Executou passos para calcular e interpretar probabilidades para eventos específicos.


