Când te ocupi de analiza datelor, vei da repede de necesitatea de a identifica corelații între diferite variabile. În acest tutorial, îți voi arăta cum să realizezi o analiză de contingensă în Excel pentru a cuantifica relația dintre două variabile nominale. Pentru asta, vom folosi un exemplu practic din industria de furnizare auto pentru a înțelege cum poți obține informații valoroase din date.
Cele mai importante constatări
- Analiza de contingensă permite investigarea relațiilor între două variabile nominale.
- Coeficientul de contingensă cuantifică puterea relației.
- Un tabel pivot în Excel este un instrument esențial pentru analiză.
Ghid pas cu pas pentru analiza de contingensă
Pasul 1: Pregătirea datelor
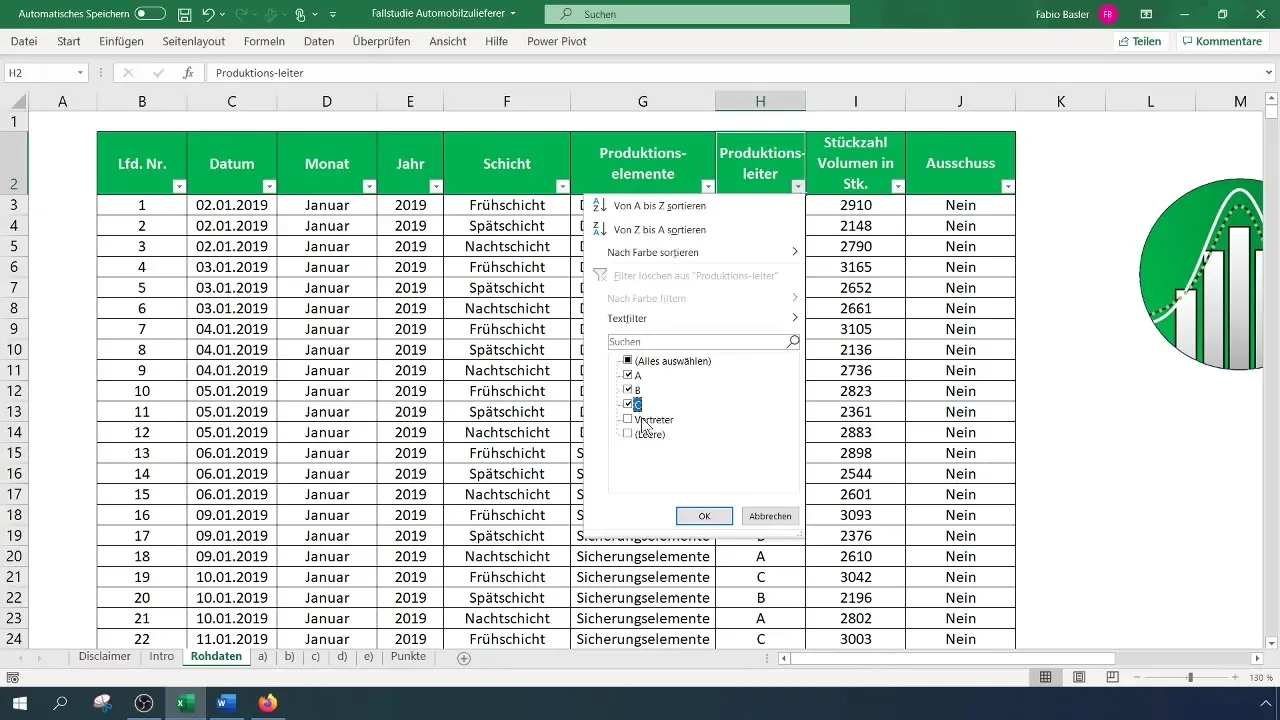
Înainte de a începe analiza de contingensă în Excel, trebuie să te asiguri că datele cu care lucrezi sunt corect pregătite. Șterge toate setările de filtrare pentru a garanta o vedere completă a datelor.
Creează un sumar care să includă managerul de producție și informațiile despre rebuturi ca date nominale. În cazul nostru, ne concentrăm pe liderii de schimb A, B și C și excludem toți ceilalți reprezentanți.
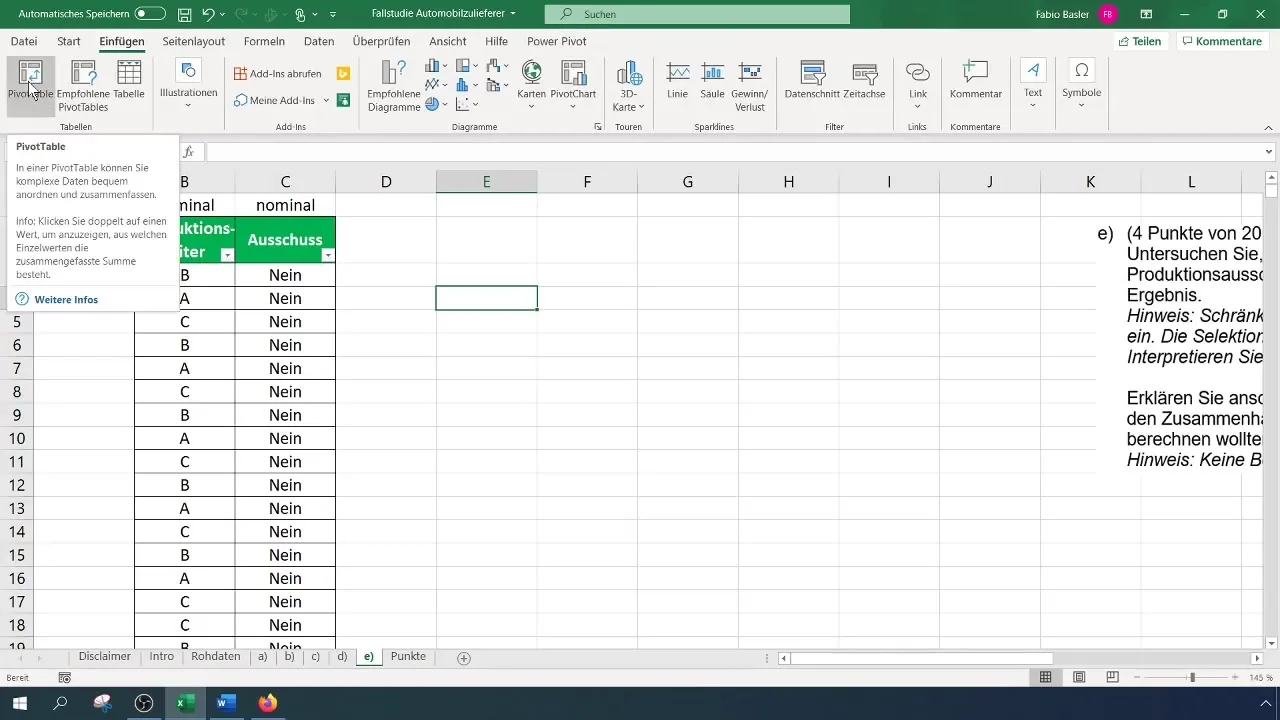
Pasul 2: Crearea tabelului pivot
Pentru a realiza analiza de contingensă, trebuie să creezi o distribuție de frecvență bidimensională care îți arată câte combinări de manager de producție și rebut apare de câte ori. Mergi în bara de meniu la "Inserare" și selectează "Tabel pivot".
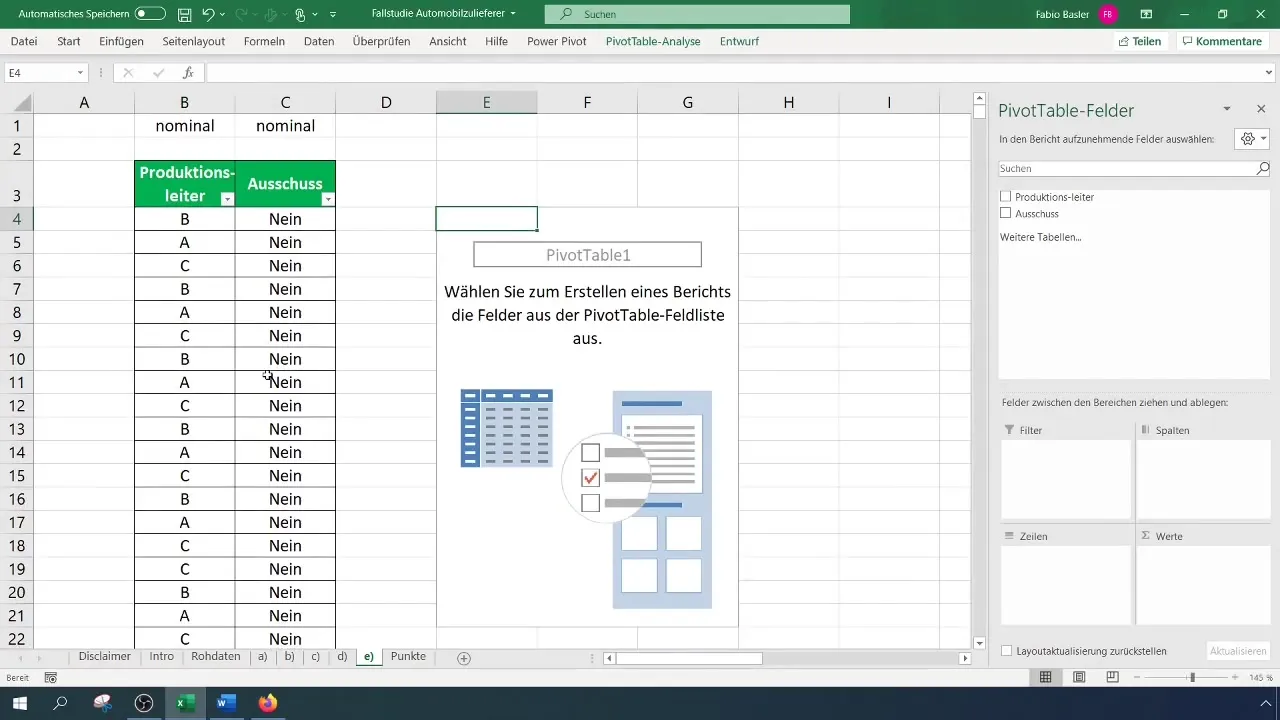
Selectează intervalul de date relevant și confirmă că titlurile sunt recunoscute corect. Tabelul tău pivot va fi acum creat și poți compara câmpurile pentru managerul de producție și rebut.
Pasul 3: Analiza frecvențelor
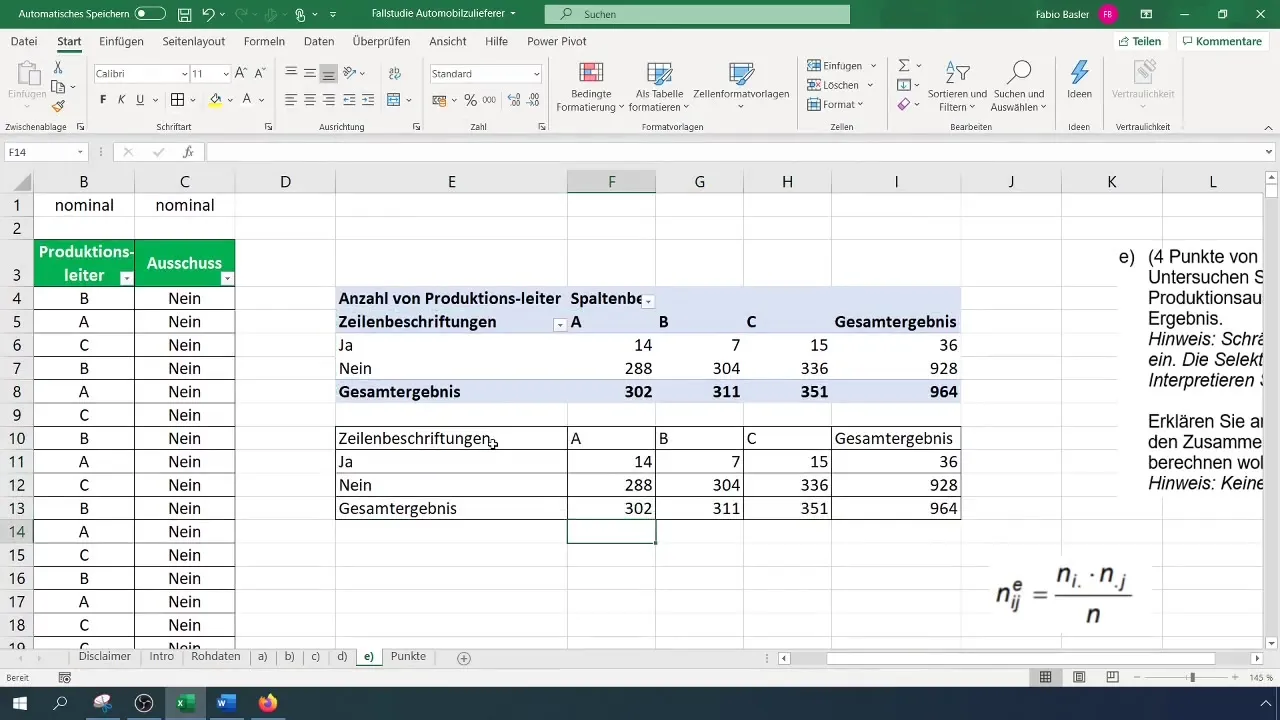
După ce ai creat tabelul pivot, poți determina frecvențele absolute. Plasează caracteristicile în rânduri și coloane în tabelul pivot. Acest lucru îți arată câte rebuturi au apărut pe fiecare manager de schimb.
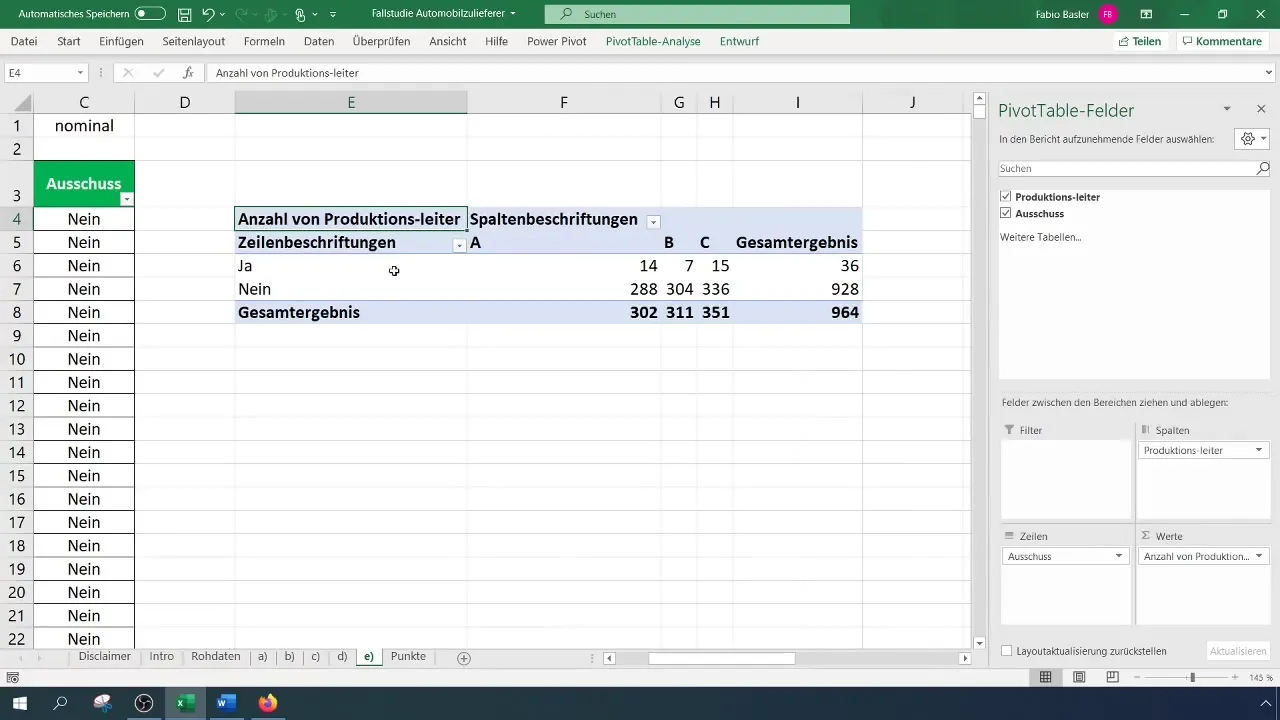
Analizează tabelul pivot și rezultatele sale. Ai grijă în special la distribuția variabilelor pentru a identifica la ce manager de schimb se întâmplă cel mai des sau cel mai rar rebuturile.
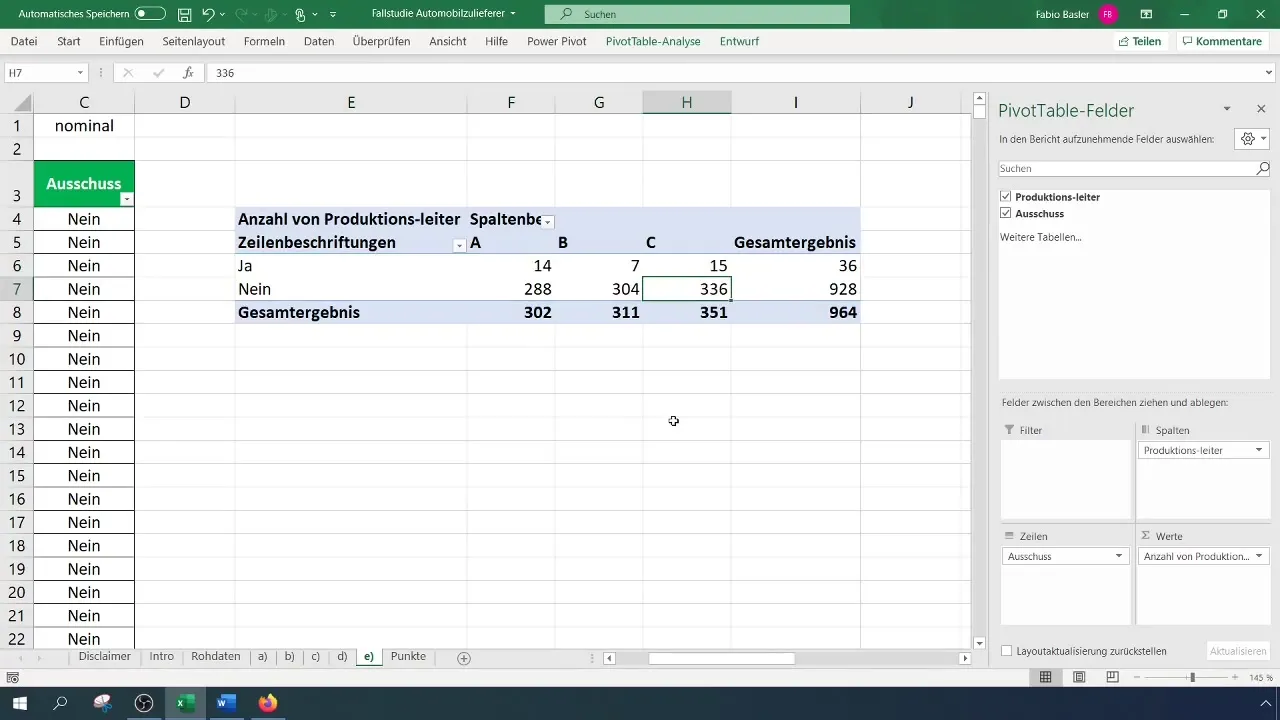
Pasul 4: Calcularea frecvențelor așteptate
Pentru a calcula coeficientul de contingensă, trebuie să determini frecvențele absolute așteptate. Formula generală este: (N_{ij} = \frac{(R_i \times C_j)}{N}), unde (R) reprezintă frecvența marginală a rândurilor iar (C) reprezintă frecvența marginală a coloanelor.
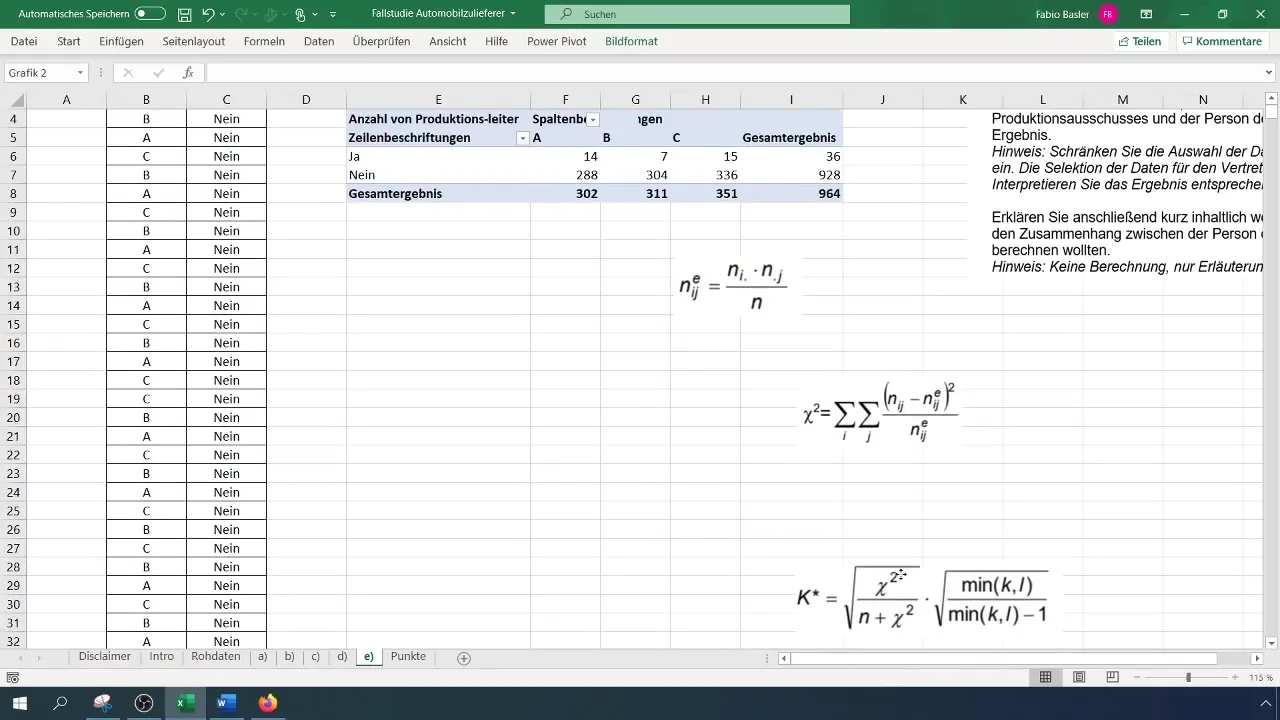
Aplică aceste calcule pe valorile din tabelul pivot. Asigură-te că creezi un tabel separat pentru frecvențele așteptate pentru a ține analizele ordonate.
Pasul 5: Calcularea valorii Chi-pătrat
Calculează acum valoarea Chi-pătrat pentru a evalua relația între variabile cantitativ. Formula este:
[ \chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}} ]
Aici (O) este frecvența observată iar (E) este frecvența așteptată.
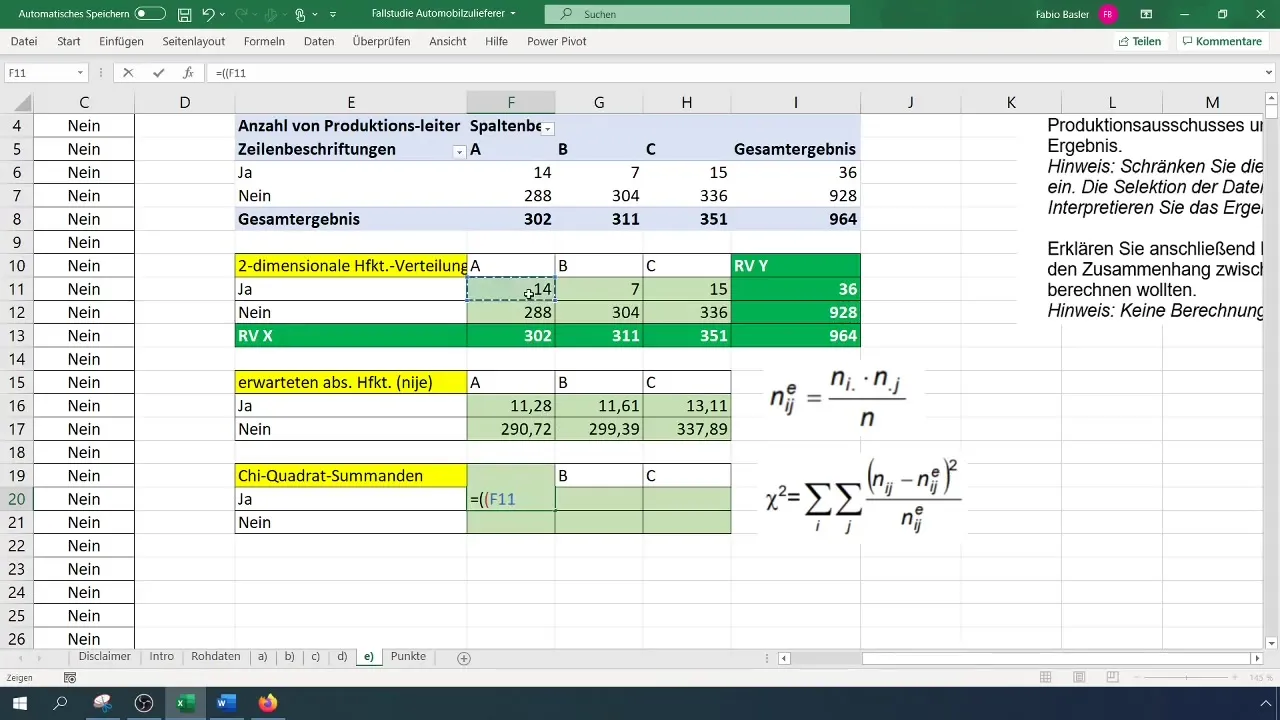
Calculează diferențele dintre frecvențele observate și cele așteptate și ridică-le la pătrat.
Pasul 6: Calcularea coeficienților de contingensă
Ultimul pas constă în calcularea coeficientului de contingensă. Formula de calcul este:
[ K = \sqrt{\frac{\chi^2}{N}} ]
Folosește valoarea chi-pătrat calculată anterior și numărul total de observații (N).
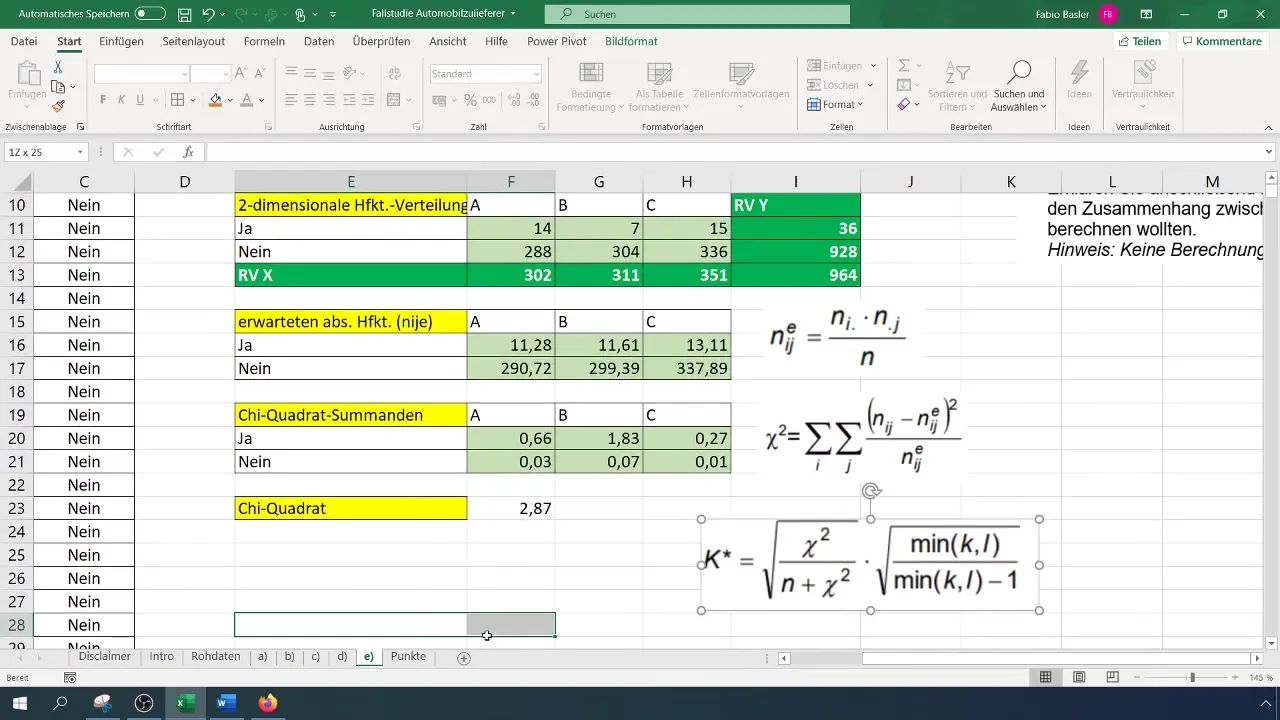
După ce ai calculat coeficientul de contingensă, poți interpreta rezultatul. Analiza noastră ne arată că coeficientul de contingensă de 0,077 indică o corelație slabă între variabile.
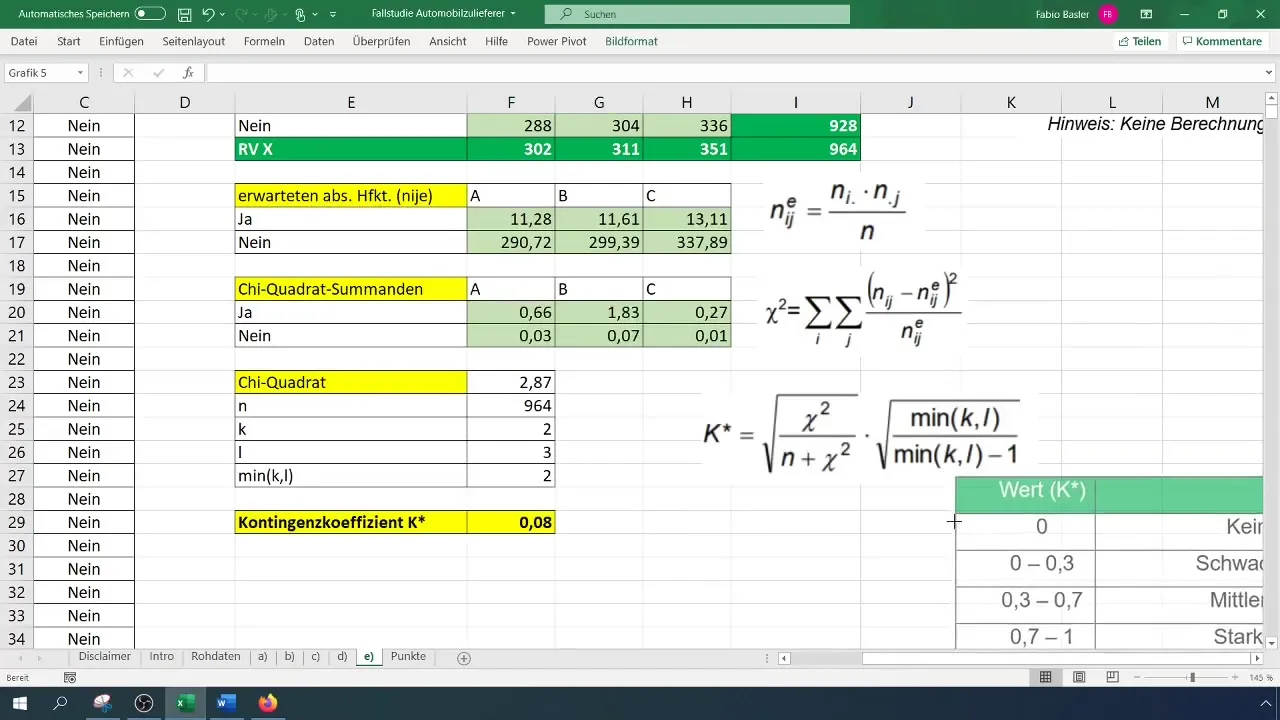
Pasul 7: Interpretarea rezultatelor
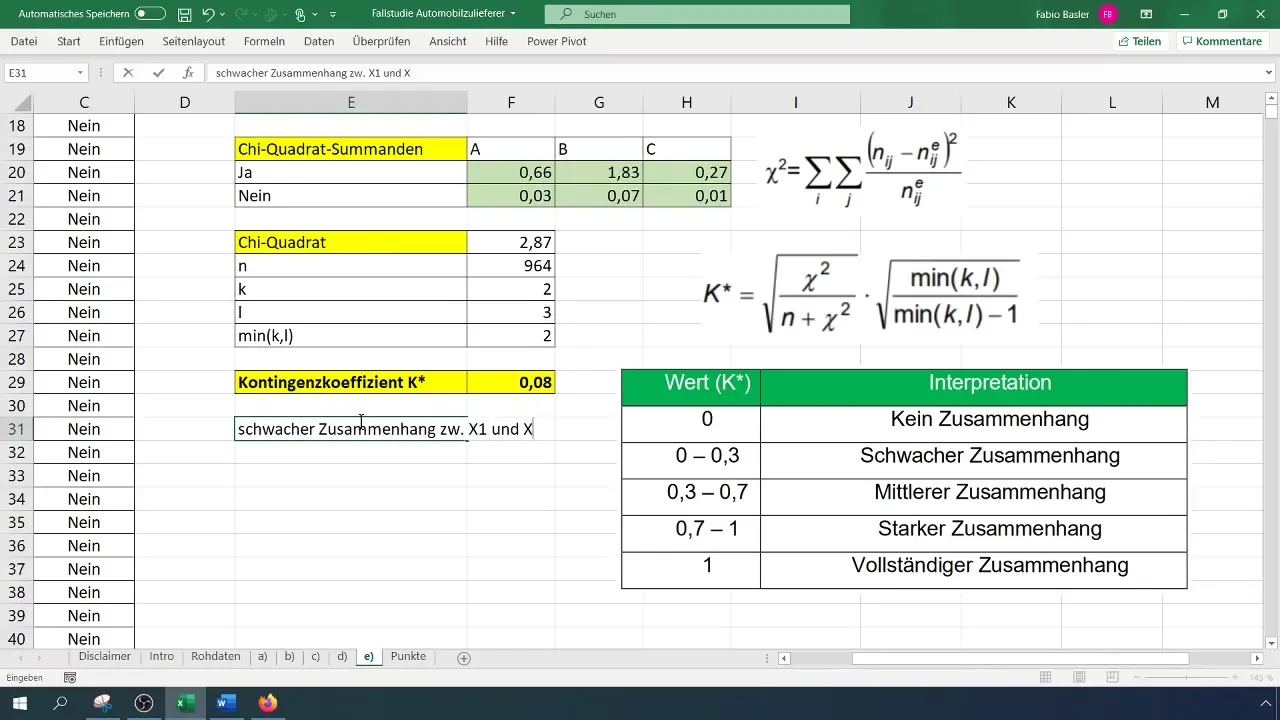
Ultimele etape ale analizei tale constau în interpretarea rezultatelor. Un coeficient de contingensă aproape de 0 arată că există puțină corelație între variabile. O valoare de 0,08 sugerează că șeful de producție nu are un impact semnificativ asupra apariției de material defectuos.
Rezumat
În acest ghid ai învățat cum să realizezi analiza de contingință în Excel pentru a identifica corelațiile dintre variabile nominale. Ai învățat cum să-ți pregătești datele, să creezi un tabel pivot și să efectuezi calculele necesare pentru coeficientul de contingensă.
Întrebări frecvente
Cum să gestionez un volum mare de date?Dacă lucrezi cu multe valori, clasifică datele în grupuri pentru a simplifica analiza.
Pot efectua analiza de contingință în alte instrumente software?Da, principiile de bază ale analizei de contingință sunt aplicabile în multe programe de statistică și limbaje de programare, chiar dacă pașii pot varia.
Care variabile sunt potrivite pentru analiza de contingință?Variabilele nominal-escalară sunt ideale pentru acest tip de analiză, deoarece nu au o ordine de rang.
Cum interpretez coeficientul de contingensă?O valoare între 0 și 0,3 indică o corelație slabă, între 0,3 și 0,6 una moderată, iar peste 0,6 una puternică.


