Testul de potrivire Chi-pătrat pentru distribuția normală cu Excel

Testul de ajustare Chi-^2 reprezintă o metodă simplă de a verifica ipoteza dacă un set de date dat urmează o distribuție normală. În acest ghid vei învăța cum să efectuezi testul Chi-^2 în Excel pentru a determina dacă vânzările de smartphone-uri corespund unei distribuții normale. Vom parcurge pas cu pas procesul, începând de la crearea unei tabele de frecvență clasată până la calcularea valorii testului și compararea acesteia cu valoarea critică a lui Chi-^2.

Concluzii cheie

• Testul de ajustare Chi-^2 ajută la testarea distribuțiilor normale.
• Este important să creezi o tabelă de frecvență clasată.
• Valoarea testului este comparată cu o valoare critică pentru a respinge sau a accepta ipoteza nulă.

Ghid pas-cu-pas

Pasul 1: Pregătirea datelor

Pentru a efectua testul Chi-^2, ai nevoie inițial de date. Copiază vânzările smartphone-urilor într-o foaie de calcul Excel. Asigură-te că datele tale sunt organizate într-o singură coloană.

Pasul 2: Crearea unui histogram

Pentru a obține primele indicii vizuale cu privire la distribuție, creează un histogram al datelor tale. Mergi la „Inserare” și selectează „Diagrame”. Adaugă un histogramă selectând intervalul datelor.

Pasul 3: Crearea tabelei de frecvență clasată

Pentru testul Chi-^2 ai nevoie de o tabelă de frecvență clasată. În primul rând, stabilește numărul de clase pentru tabela ta - în acest caz, vom folosi șase clase. Calculează lățimea intervalelor și creează tabela în consecință.

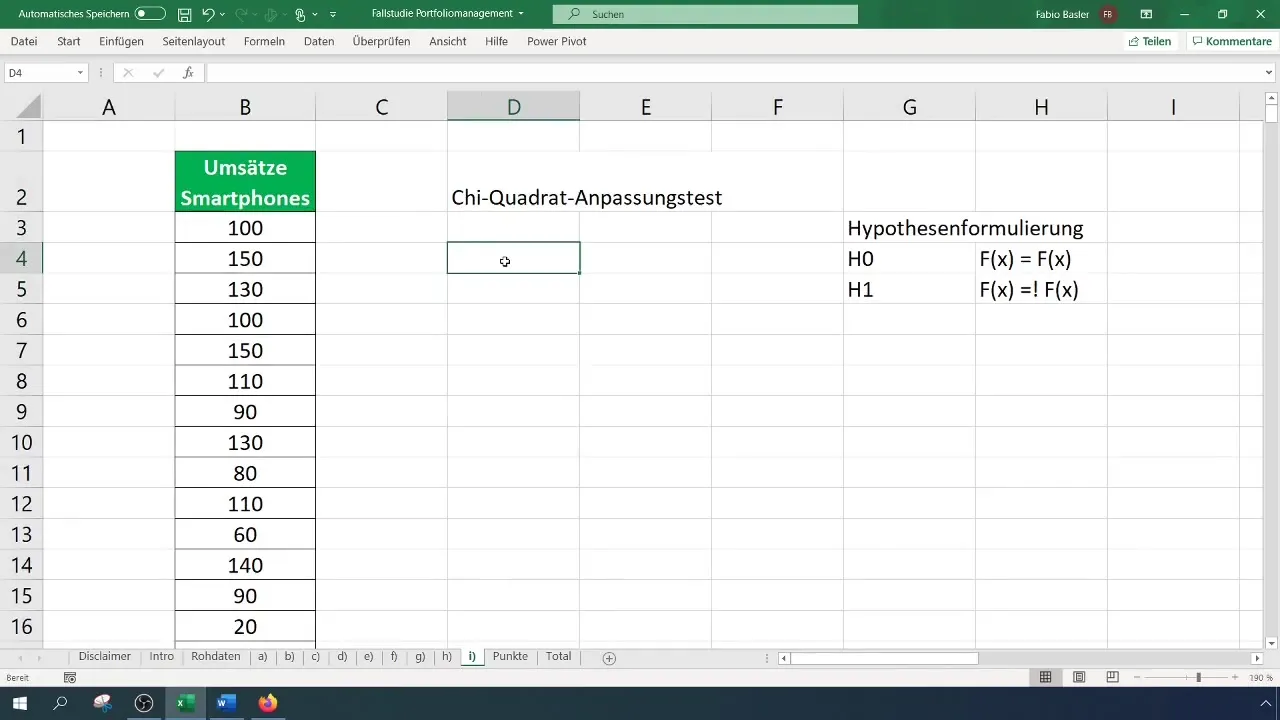
Pasul 4: Calcularea frecvențelor

Acum trebuie să calculezi frecvențele observate pentru fiecare clasă. Mergi la „Analiza datelor” din meniu și selectează „Histogramă”. Alege intervalul de intrare pentru datele tale și limitele claselor. Stabilește intervalul de ieșire pentru tabela de frecvență.

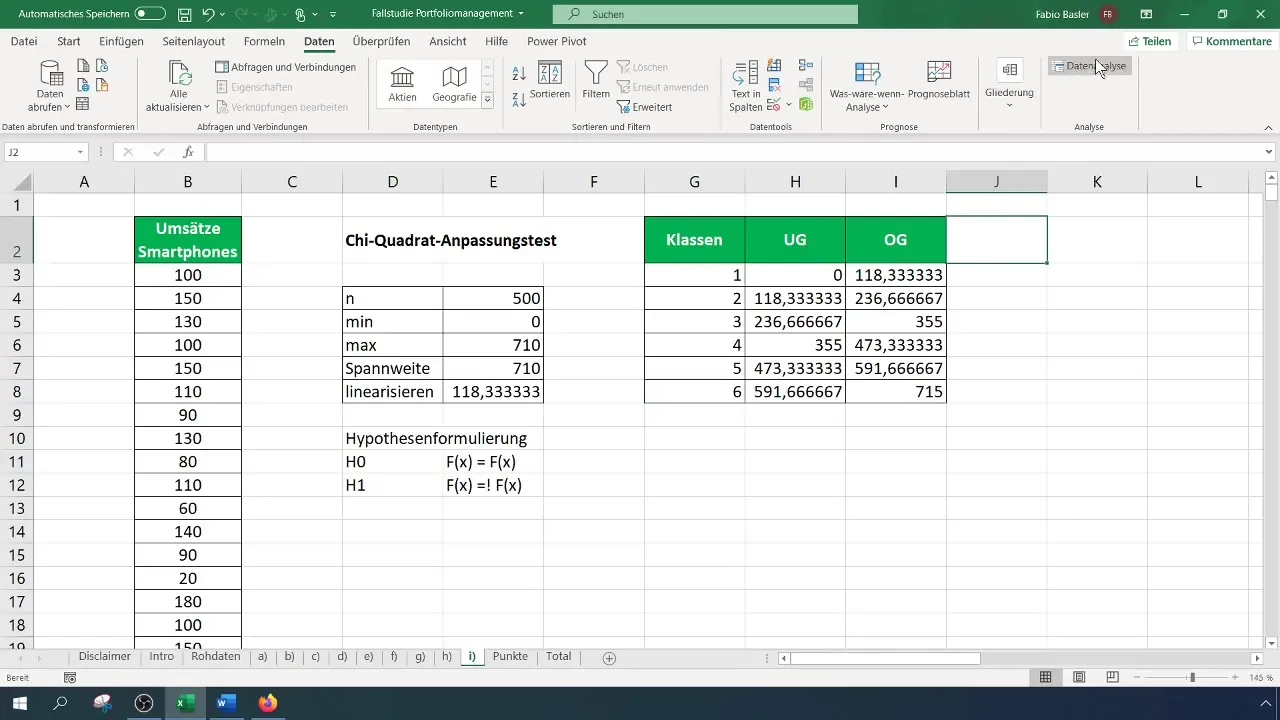
Pasul 5: Calcularea frecvențelor estimate

Pentru a estima frecvențele, calculează probabilitățile pentru fiecare clasă pe baza presupusei distribuții normale. Pentru acest lucru, ai nevoie de valoarea medie și deviația standard a datelor tale.

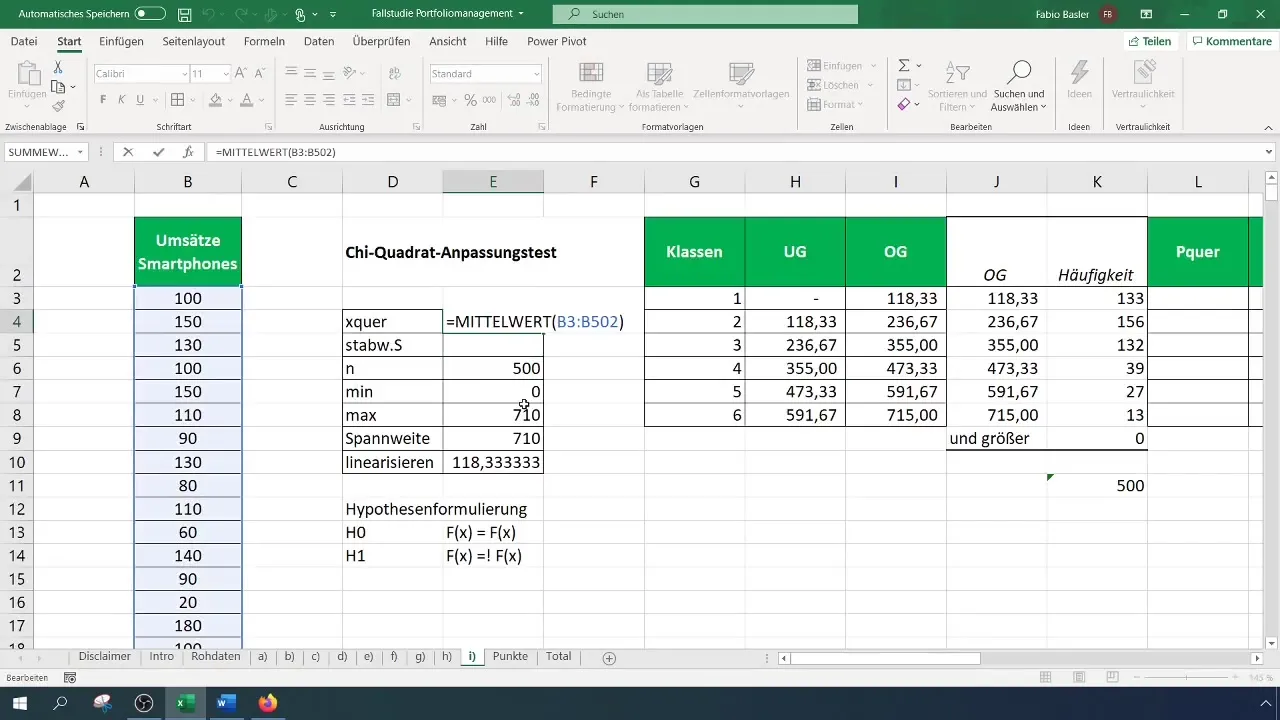
Pasul 6: Calcularea valorii testului

Calculează valoarea testului (Chi-^2) folosind formula:

[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]

unde (O_i) sunt frecvențele observate și (E_i) sunt frecvențele estimate. Poți efectua această calculație în Excel stocând componente individuale în celule separate.

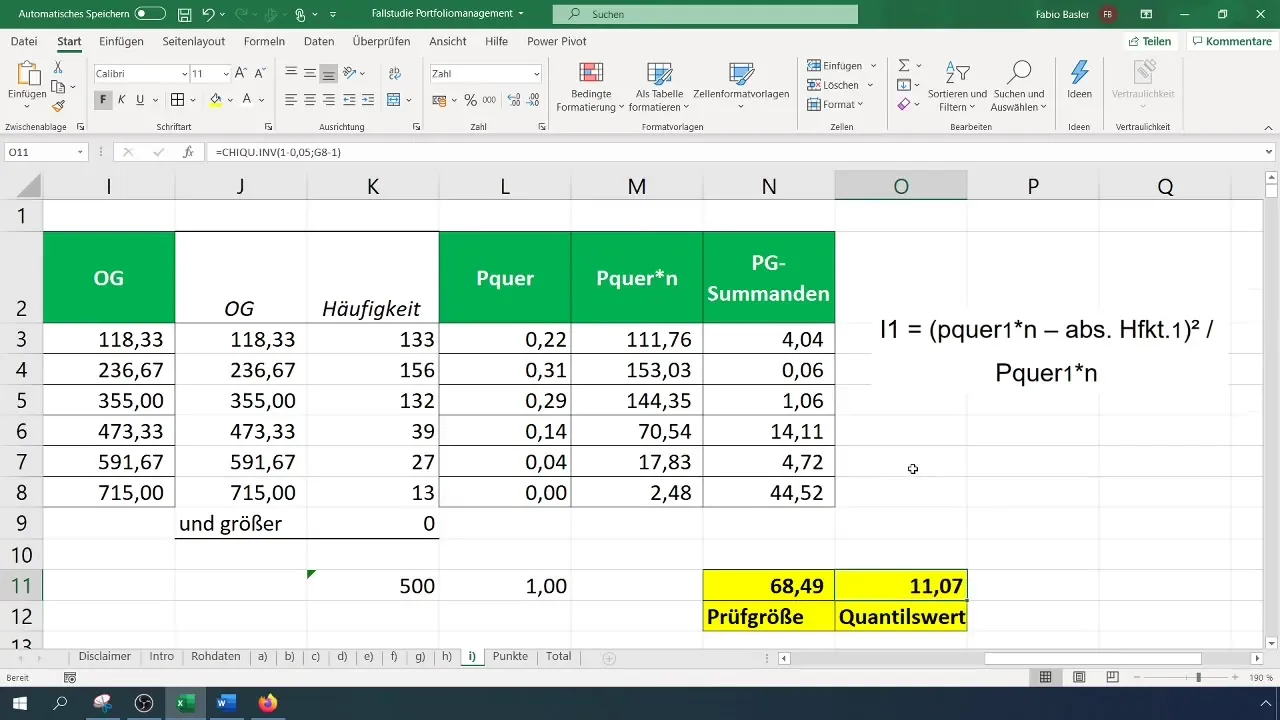
Pasul 7: Calcularea valorii critice

Pentru a evalua valoarea testului, trebuie să calculezi valoarea critică ( \chi^2 ) pentru nivelul tău de încredere și numărul de grade de libertate. Numărul de grade de libertate pentru testul Chi-^2 este (k - 1), unde (k) reprezintă numărul de clase.

Pasul 8: Verificarea ipotezelor

Compară valoarea testului calculată cu valoarea critică. Dacă valoarea testului este mai mare decât valoarea critică, respinge ipoteza nulă, ceea ce înseamnă că datele nu sunt distribuite normal. În caz contrar, accepți ipoteza nulă.

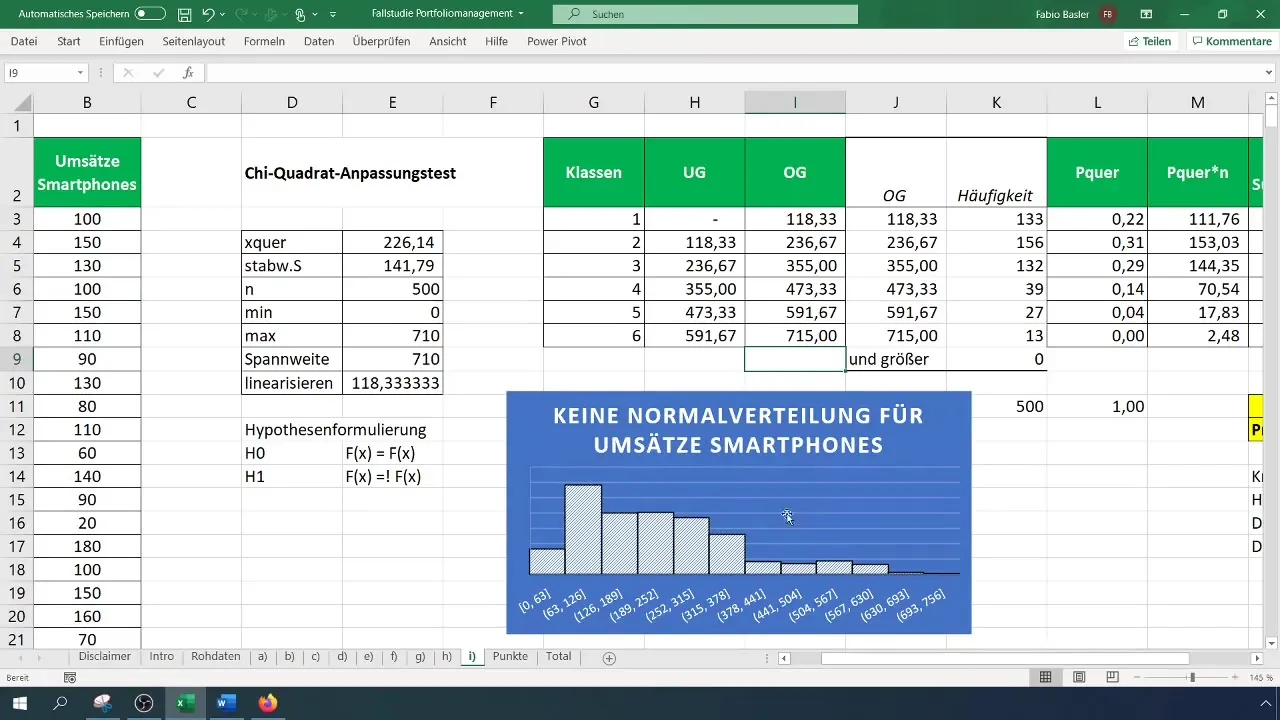
Pasul 9: Rezumatul rezultatelor

Păstrează-ți rezultatele și extinde-le cu datele grafice și testele de ipoteze. Nu uita să verifici histograma pentru a confirma vizual că distribuția nu este normală.

Rezumat

În cursul acestui ghid, ai învățat cum să realizezi testul de ajustare Chi-Pătrat în Excel pentru a analiza distribuția normală a vânzărilor de smartphone-uri. Pașii includ crearea unei tabele de frecvențe clasificate, calculul frecvențelor așteptate, a mărimii testului și în cele din urmă compararea acestora cu valoarea critică.