Успешный 1-SP-тест математического ожидания в Excel

Статистические тесты являются центральной частью анализа данных и принятия решений. Особенно в области биотехнологии может быть решающим проверка гипотез о успешности лекарственных веществ. В рамках этого учебного пособия вы узнаете, как провести односторонний тест (1-SP-тест) для математического ожидания с известной дисперсией эффективно в Excel .

Основные выводы

Это руководство предоставляет вам:

• Теоретические основы 1-SP-теста.
• Шаги по выполнению теста в Excel.
• Интерпретацию результатов.

Подготовка данных

Для проведения 1-SP-теста в Excel сначала вам понадобятся соответствующие данные. В нашем примере мы предполагаем, что вы анализируете успеваемость лекарственных веществ. Известно, что средний уровень успешности ранее составлял 59%, с стандартным отклонением 19. Сначала вам следует занести ваши данные в таблицу Excel.

Убедитесь, что ваши данные организованы в столбцы, чтобы позже вы могли получить к ним доступ. Хорошая структурированность поможет вам легче следовать каждому шагу.

Обзор теста

1-SP-тест служит для проверки, отличается ли среднее значение успешности значительно от заданного значения. В данном случае мы проверяем, можно ли заметно увеличить успешность до 59% в будущем.

Формулирование гипотез

Формулирование гипотез, которые вы предполагаете проверить в тесте, имеет решающее значение:

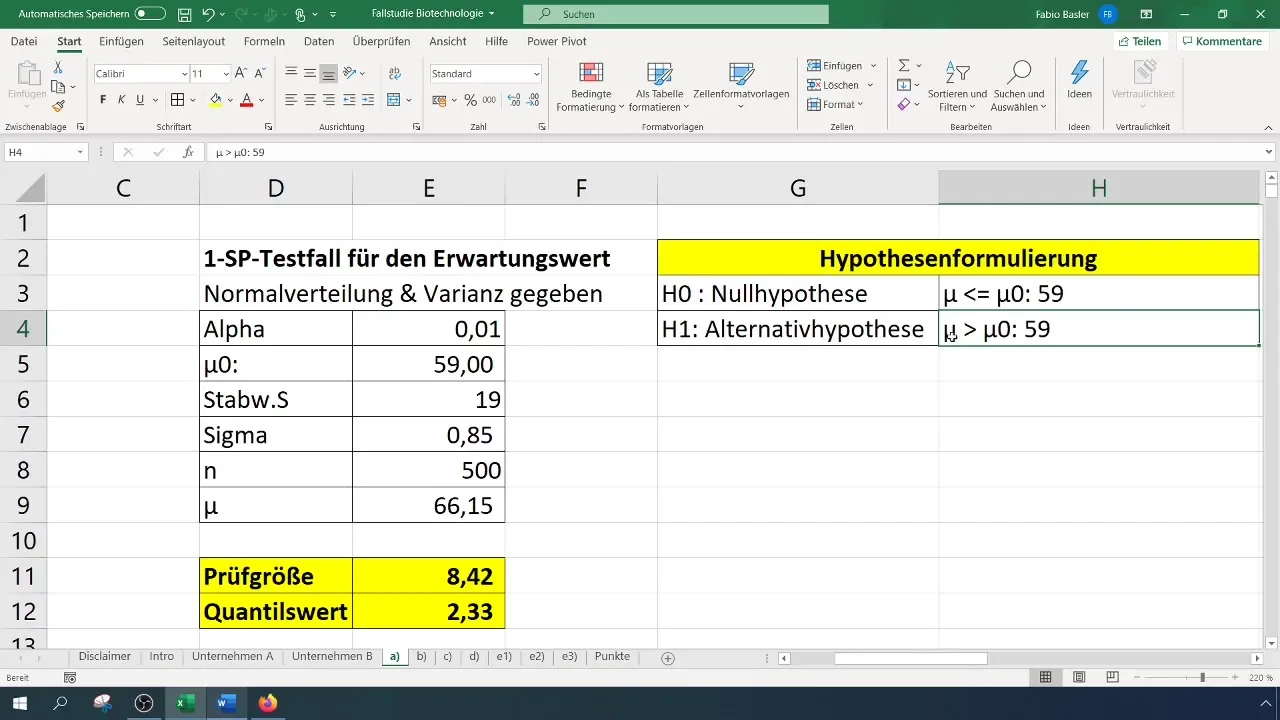
• Нулевая гипотеза (H0): Истинное математическое ожидание равно 59 (σ = 59%).
• Альтернативная гипотеза (H1): Истинное математическое ожидание больше 59%.

При формулировании гипотез важно понимать, что именно должно быть протестировано и как это будет выражено в вашем контексте.

Важно четко видеть разницу между нулевой гипотезой и альтернативной гипотезой, поскольку они являются основой для последующих вычислений.

Отбор выборки

Для нашего теста мы берем выборку из 500 лекарственных веществ. Важно отметить, что выборка должна быть репрезентативной и должна быть гарантирована подходящим методом, чтобы ваши результаты можно было реалистично перенести на всю популяцию.

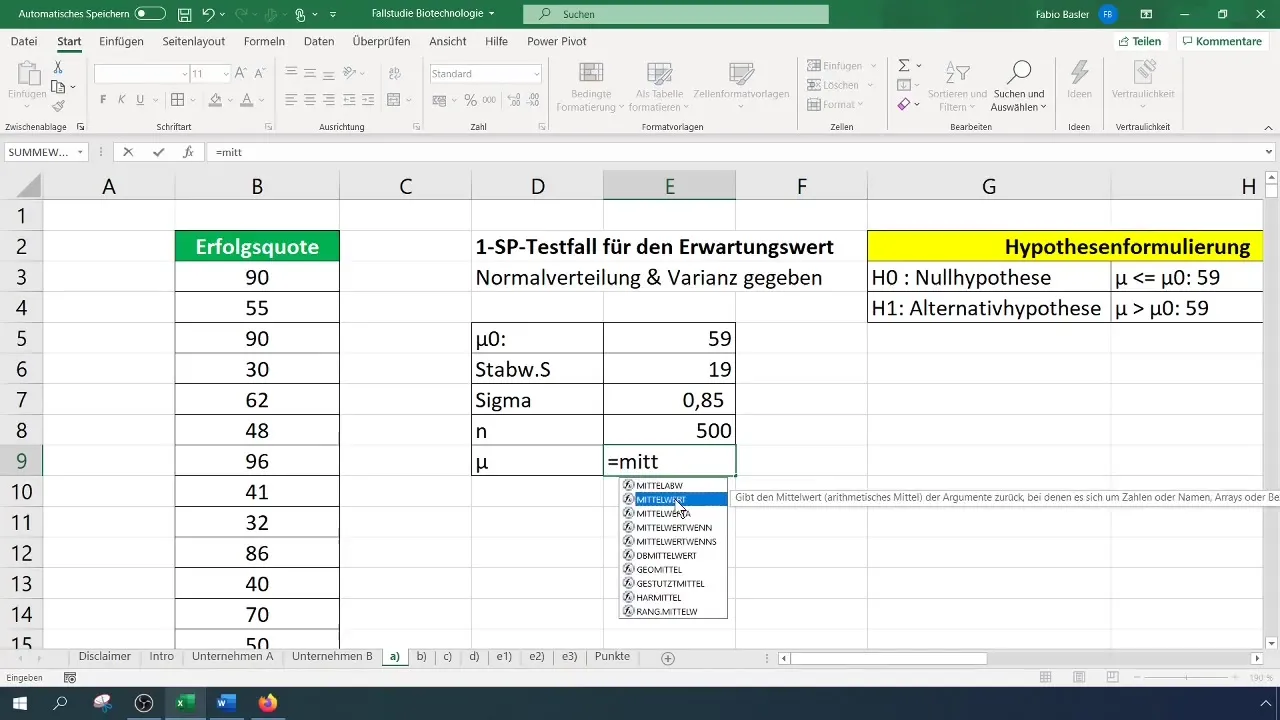
Для теста сначала рассчитайте арифметическое среднее значение. Это должно быть просто сделать в Excel, используя соответствующую формулу.

Определение размера проверки

Размер проверки для 1-SP-теста определяется следующей формулой:

[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]

Здесь (\bar{x}) - среднее вашей выборки, (\mu_0) - предполагаемое среднее значение (в данном случае 59), (\sigma) - стандартное отклонение (здесь 19), а (n) - количество выборок (500).

После подстановки значений в формулу рассчитайте размер проверки, чтобы определить, является ли он значимым или нет.

Определение критического значения

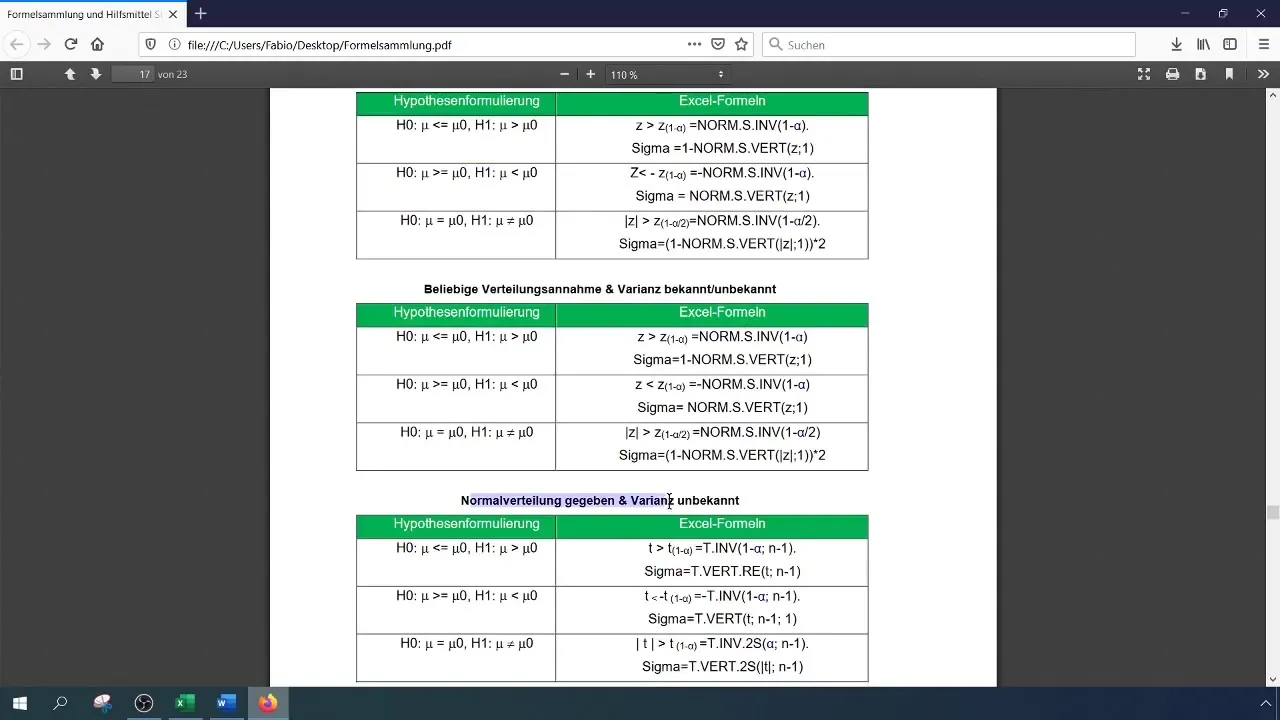
Для уровня значимости 1% (0,01) вам нужно прочитать или рассчитать критическое значение. Это можно сделать в Excel с помощью функции NORM.S.INV.

Формула выглядит следующим образом:

[ \text{NORM.S.INV}(1 - \alpha) ]

Здесь (\alpha) - уровень значимости (0,01). Полученное значение будет использовано для сравнения с размером проверки.

Проведение теста

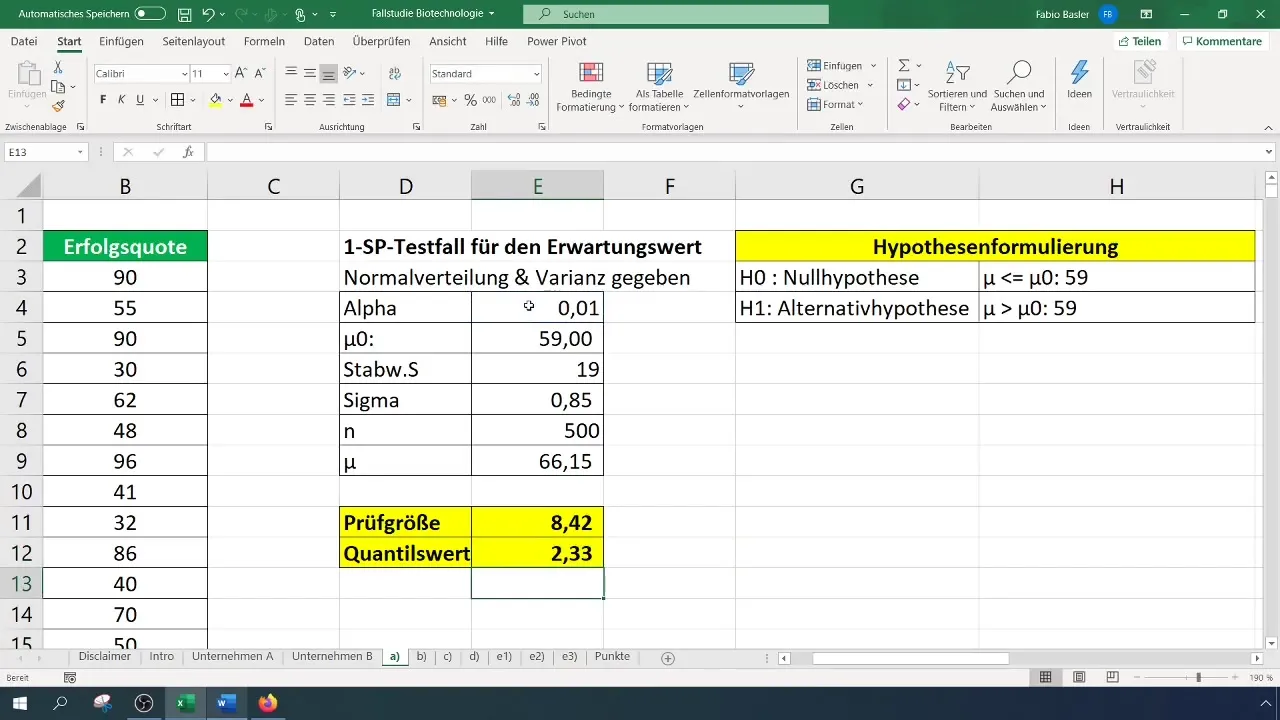
После того как у вас есть и размер проверки, и критическое значение, сравните их:

• Если размер проверки больше критического значения, то нулевая гипотеза отклоняется.
• В противном случае вы не можете отклонить нулевую гипотезу.

В нашем случае статистический критерий составляет 8,4, что превышает критическое значение 2,33. Поэтому мы можем отклонить нулевую гипотезу. Это свидетельствует о значительном улучшении процента успешных результатов.

Интерпретация результатов

После того как вы провели тест и получили результаты, вам следует ясно интерпретировать их в конкретном контексте. Отклонение нулевой гипотезы означает, что тестируемое новое значение значительно отличается от прошлого значения, в данном случае 59%.

Эта информация имеет огромное значение для стратегического принятия решений в вашей компании. Она подтверждает, что усилия по улучшению процента успешных результатов были эффективны.

Итог

В этом учебнике вы узнали, как провести тест на ожидаемое значение для одной выборки в Excel. На примере кейс-стади тестирования вы смогли проследить шаги от формулирования гипотез до расчета данных и интерпретации результатов. Эти знания ценны не только для научных исследований, но и для практических приложений в компании.