Тест приспособления критерия X представляет собой простой метод проверки гипотезы о том, следует ли данный ряд данных нормальному распределению. В этом руководстве вы узнаете, как выполнить тест Хи-квадрат в Excel, чтобы определить, соответствуют ли продажи смартфонов нормальному распределению. Мы будем пошагово проходить через процесс, начиная с создания классифицированной таблицы частот и заканчивая вычислением тестовой статистики и сравнением с критическим значением Хи-квадрат.
Основные выводы
- Тест адаптации критерия Хи-квадрат помогает проверять нормальные распределения.
- Важно создать классифицированную таблицу частот.
- Тестовая статистика сравнивается с критическим значением для отклонения или принятия нулевой гипотезы.
Пошаговое руководство
Шаг 1: Подготовка данных
Для проведения теста Хи-квадрат вам сначала понадобятся данные. Скопируйте продажи смартфонов в лист Excel. Убедитесь, что ваши данные организованы в один столбец.

Шаг 2: Создание гистограммы
Для получения первых визуальных указаний о распределении создайте гистограмму ваших данных. Для этого перейдите в "Вставка" и выберите "Диаграммы". Добавьте гистограмму, выбрав диапазон для данных.
Шаг 3: Создание классифицированной таблицы частот
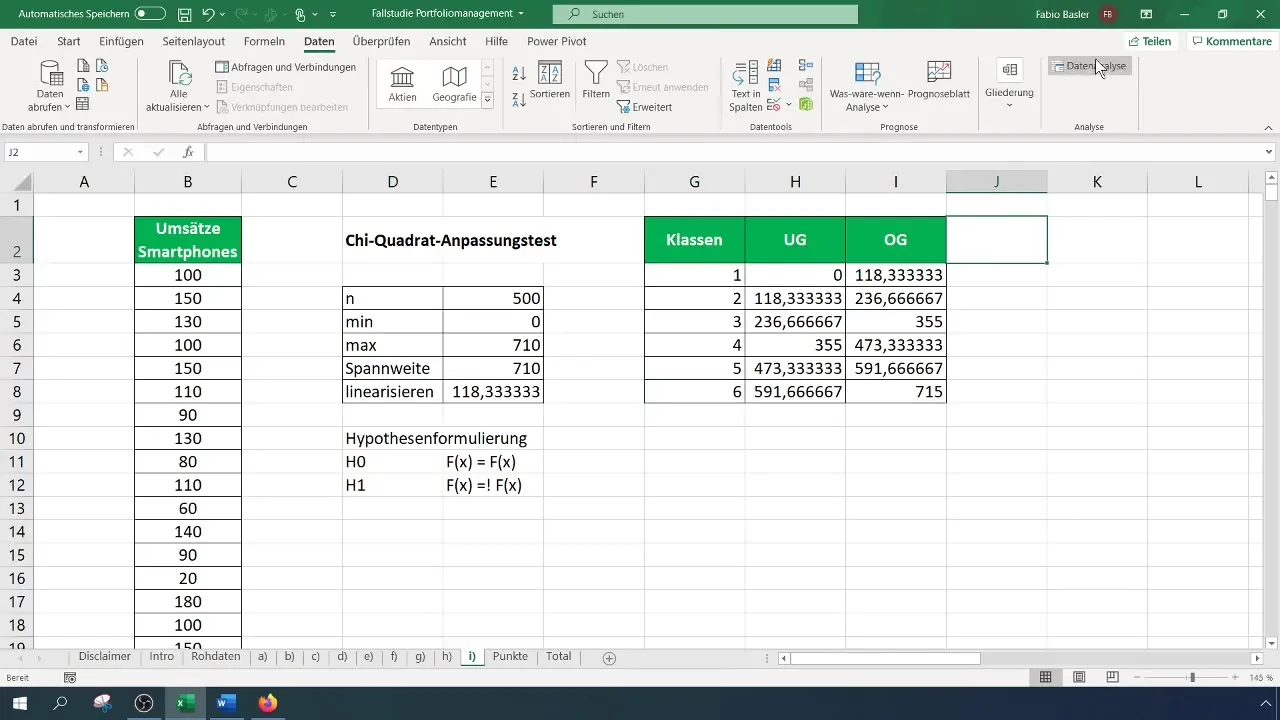
Для теста Хи-квадрат вам нужна классифицированная таблица частот. Сначала определите количество классов для вашей таблицы - в этом случае мы используем шесть классов. Рассчитайте ширину интервалов и создайте таблицу соответственно.
Шаг 4: Расчет частот
Теперь вам нужно рассчитать наблюдаемые частоты для каждого класса. Перейдите в меню "Анализ данных" и выберите "Гистограмма". Выберите диапазон ввода для ваших данных и границы классов. Определите диапазон вывода для таблицы частот.
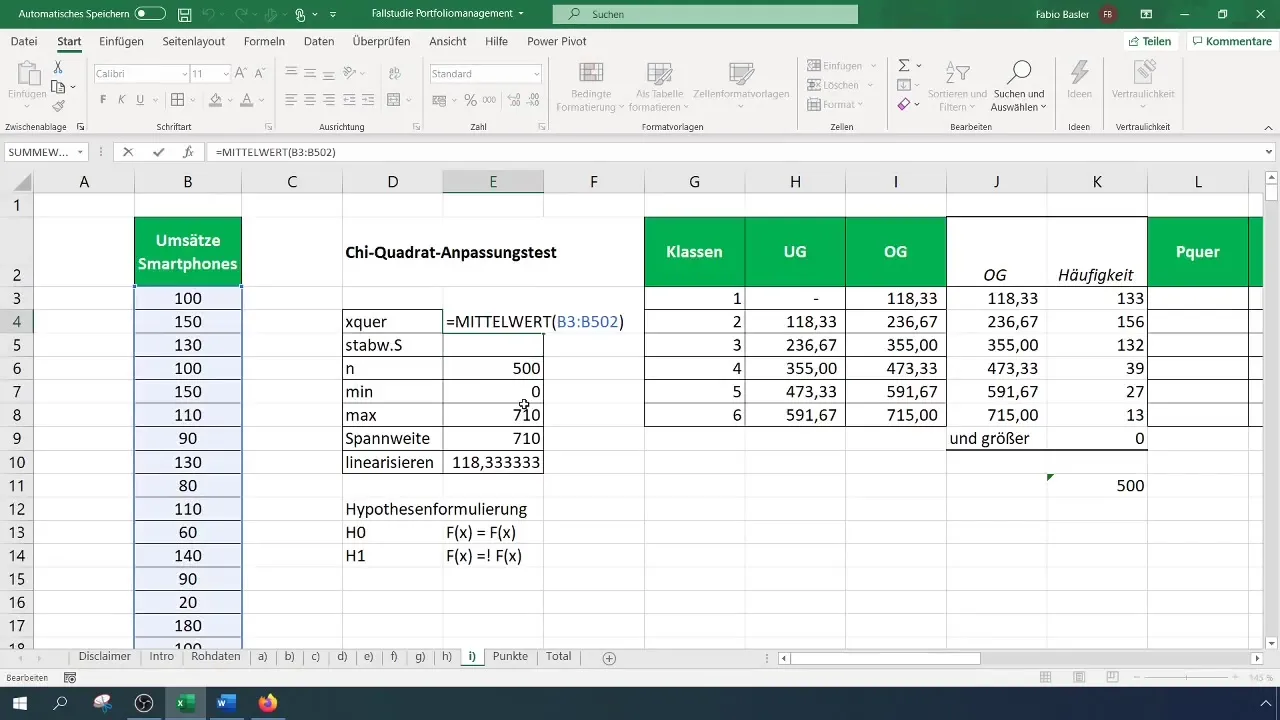
Шаг 5: Расчет ожидаемых частот
Для определения ожидаемых частот рассчитайте вероятности для каждого класса на основе предполагаемого нормального распределения. Для этого вам понадобятся среднее значение и стандартное отклонение ваших данных.
Шаг 6: Расчет тестовой статистики
Рассчитайте тестовую статистику (критерий Хи-квадрат) по формуле:
[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]
где (O_i) - наблюдаемые, а (E_i) - ожидаемые частоты. Вы можете выполнить это вычисление в Excel, сохраняя отдельные компоненты в разных ячейках.
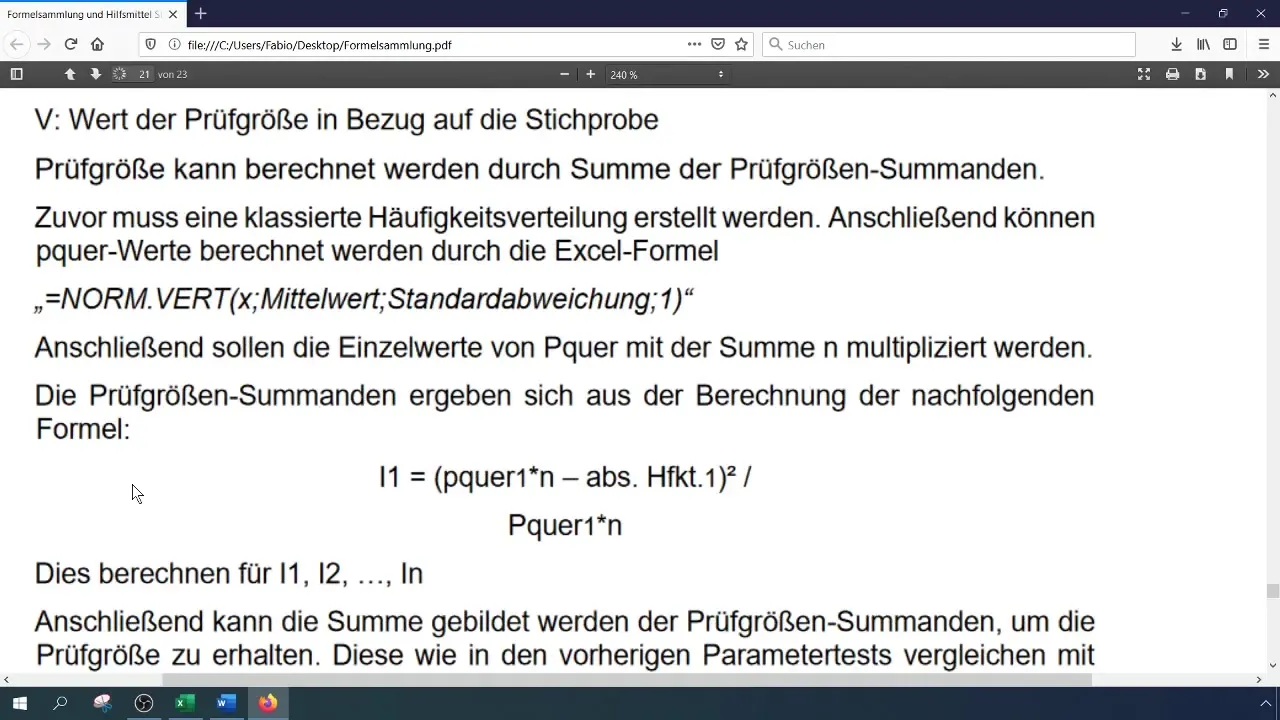
Шаг 7: Расчет критического значения
Для оценки тестовой статистики вам необходимо рассчитать критическое значение ( \chi^2 ) для вашего уровня доверия и количества степеней свободы. Количество степеней свободы для теста Хи-квадрат составляет (k - 1), где (k) - количество классов.
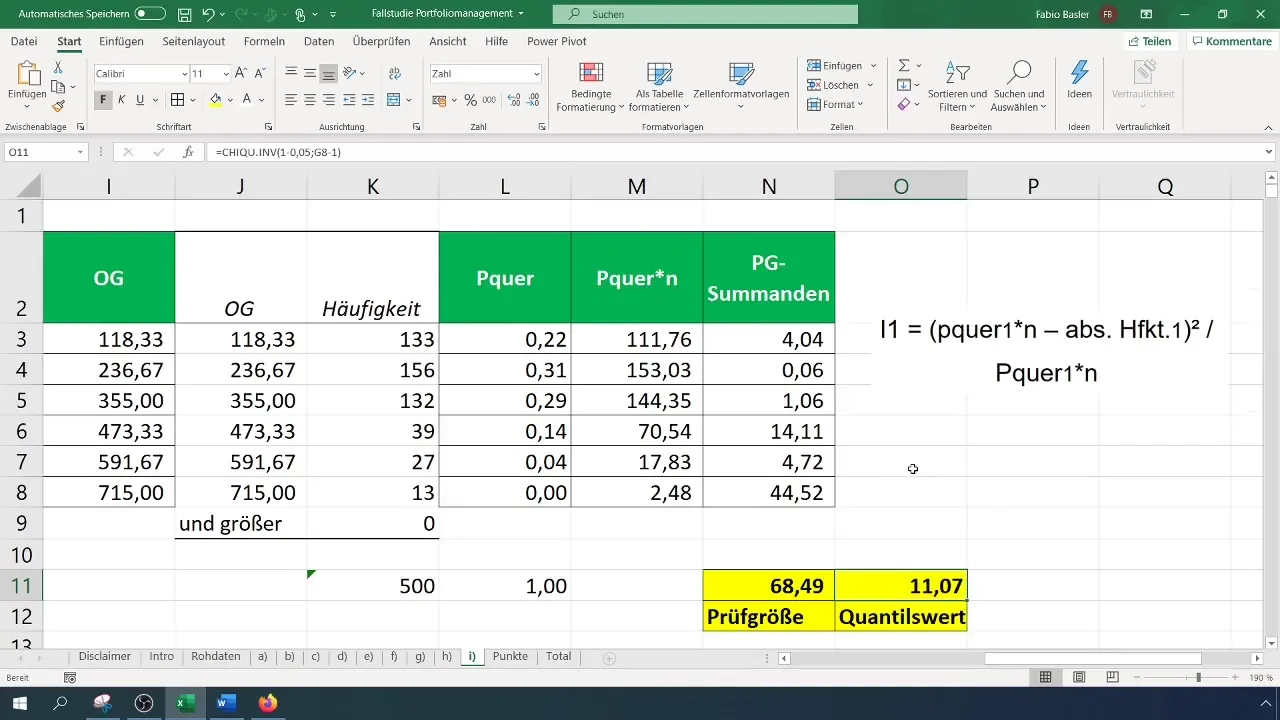
Шаг 8: Проверка гипотез
Сравните вашу рассчитанную тестовую статистику с критическим значением. Если тестовая статистика больше критического значения, отклоните нулевую гипотезу, что означает, что данные не имеют нормального распределения. В противном случае примите нулевую гипотезу.
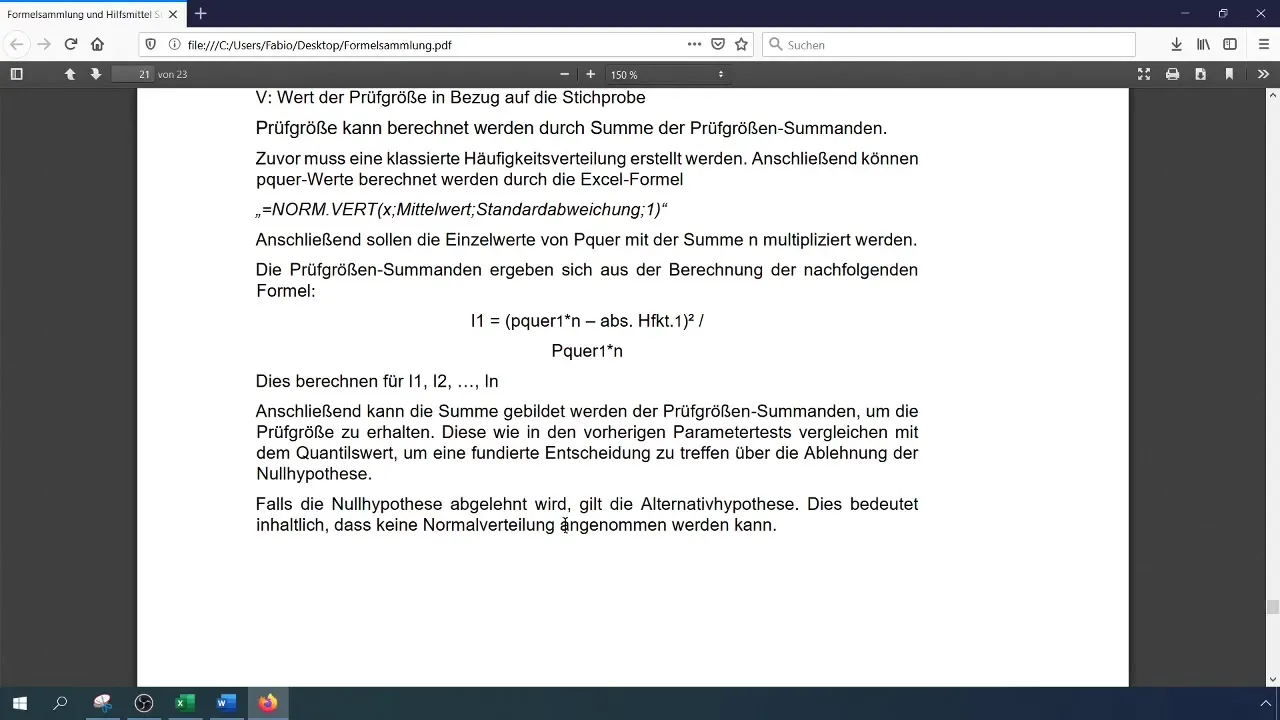
Шаг 9: Обобщение результатов
Запишите свои результаты и дополните их графическими данными и тестами гипотез. Не забудьте проверить свою гистограмму, чтобы визуально подтвердить, что распределение не является нормальным.
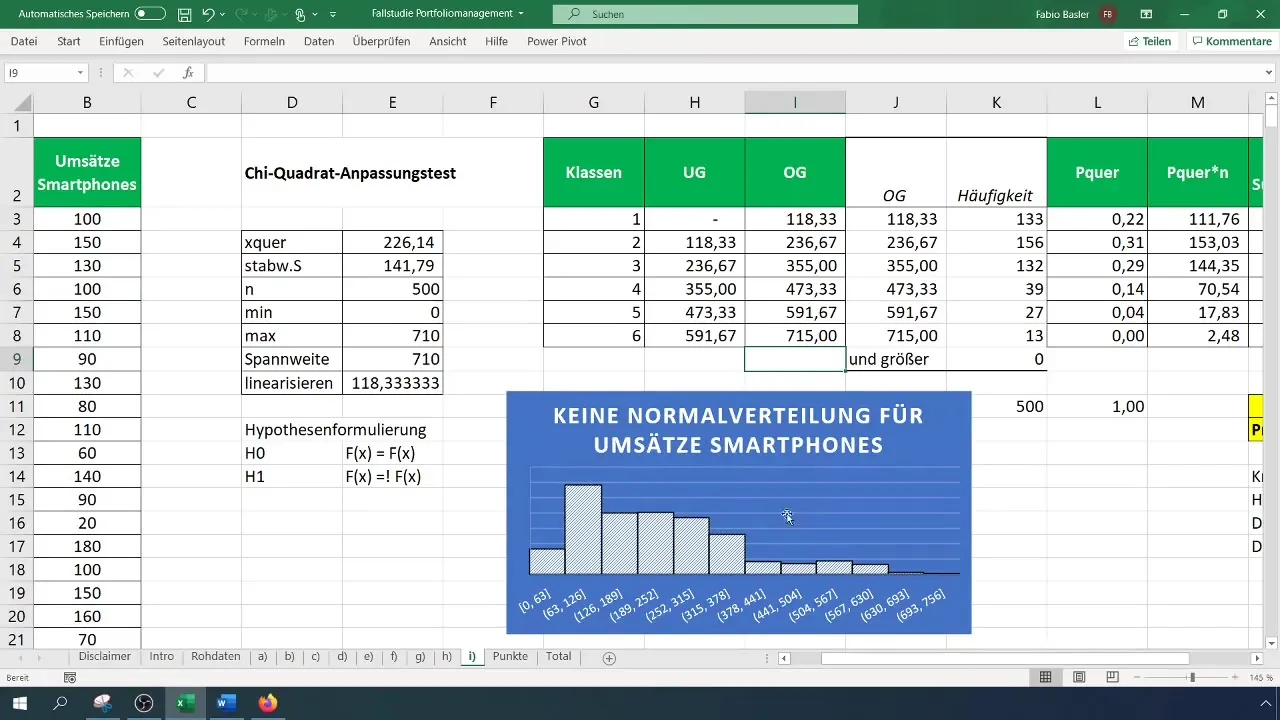
Обзор
В этом руководстве вы узнали, как выполнять тест приспособления хи-квадрат в Excel для анализа нормального распределения выручки от смартфонов. Шаги включают в себя создание таблицы частот, расчеты ожидаемых частот, тестовую статистику и, наконец, сравнение её с критическим значением.
Часто задаваемые вопросы
Что такое тест приспособления хи-квадрат?Тест приспособления хи-квадрат проверяет, соответствует ли наблюдаемое частотное распределение нормальному распределению.
Сколько классов мне необходимо для таблицы частот?Обычно требуется как минимум от 5 до 10 классов, чтобы анализ данных был информативным.
Что делать, если нулевая гипотеза отвергается?Если вы отвергаете нулевую гипотезу, это означает, что данные не имеют нормальное распределение.
Как рассчитать критическое значение хи-квадрат?Критическое значение определяется по таблице распределения хи-квадрат по степеням свободы и желаемому уровню значимости.


