Статистические анализы являются необходимым инструментом в управлении портфелем. Особенно мощным методом является регрессионный анализ, особенно когда речь идет о определении влияния нескольких независимых переменных на зависимую переменную. Хотите узнать, как построить и проанализировать линейную функциональную зависимость с помощью множественной регрессии в Excel? Это руководство предоставляет вам четкий обзор и детальное пошаговое руководство.
Основные выводы
- Регрессионный анализ помогает количественно оценить влияние независимых переменных на зависимую переменную.
- Важно оценить качество и статистическую значимость регрессионной модели.
- Исходя из оценки коэффициентов, можно определить, какая из независимых переменных оказывает более сильное воздействие на зависимую переменную.
Пошаговое руководство по регрессионному анализу в Excel
Подготовка данных
Прежде чем приступить к регрессионному анализу, необходимо подготовить данные. Зависимая переменная (y) в данном случае - это выручка от ноутбуков, а независимые переменные (x1 и x2) - количество сотрудников и количество конкурентных действий. Сначала введите все необходимые данные в Excel и структурируйте их наглядно.
Проверка корреляции
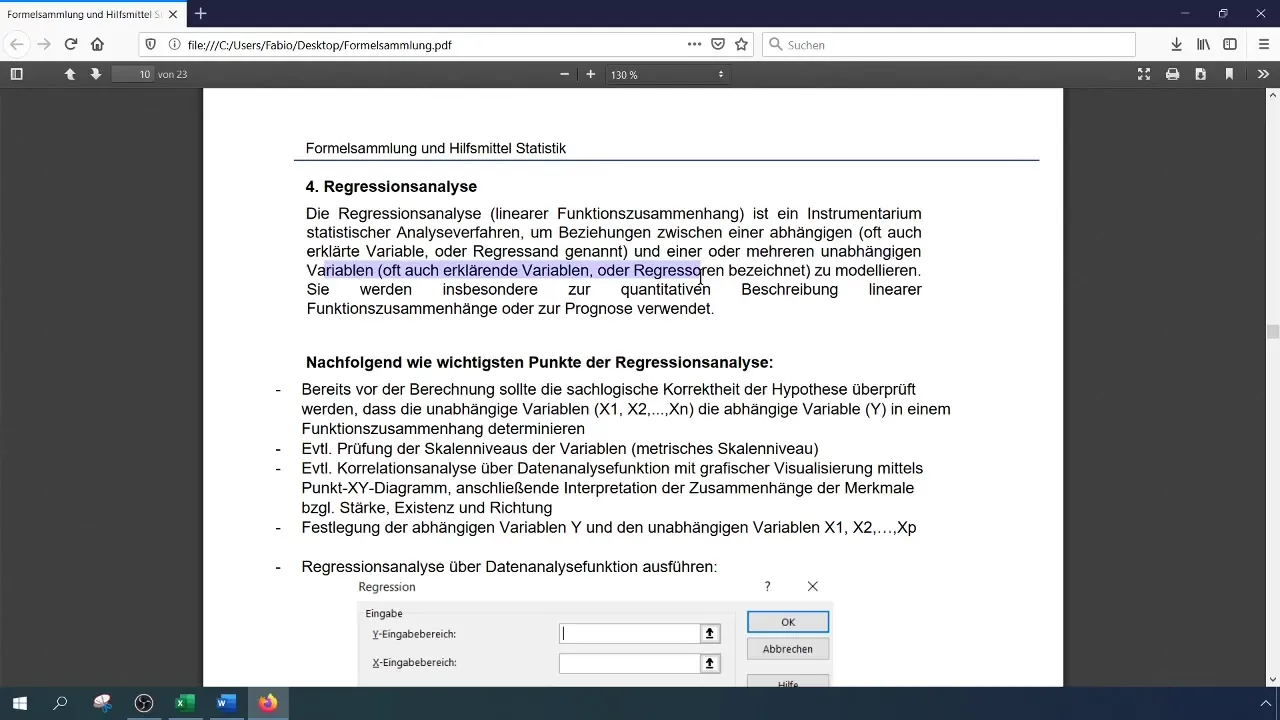
Для получения первых намеков на возможные взаимосвязи между переменными вы можете создать матрицу корреляции. Эта матрица поможет вам увидеть, насколько сильно связаны различные переменные друг с другом. Вы можете сделать это через функцию «Анализ данных» в Excel и затем выбрать матрицу корреляции, включив все необходимые диапазоны данных.
Проведение регрессионного анализа
Теперь вы готовы выполнить регрессионный анализ. Для этого снова выберите функцию «Анализ данных», затем выберите «Регрессия». Здесь вы укажите диапазон ввода для зависимой переменной (выручка от ноутбуков) и независимые переменные (количество сотрудников и конкурентные действия).
Интерпретация результатов
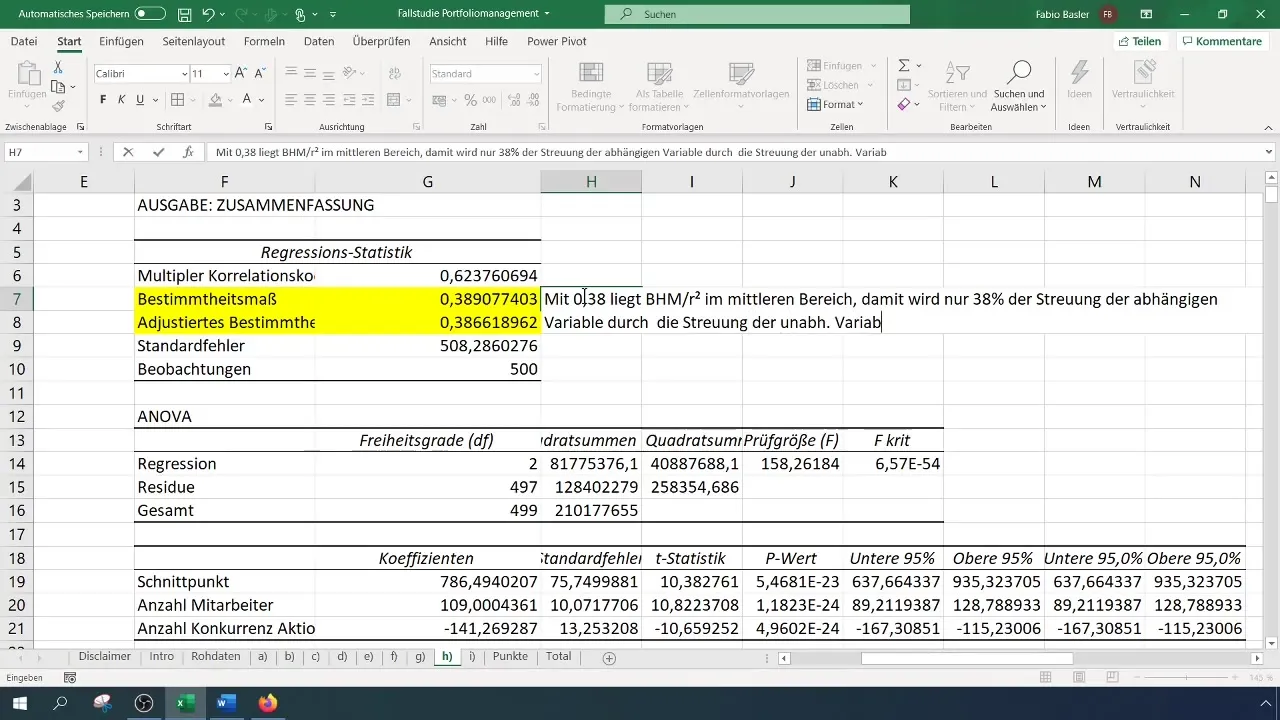
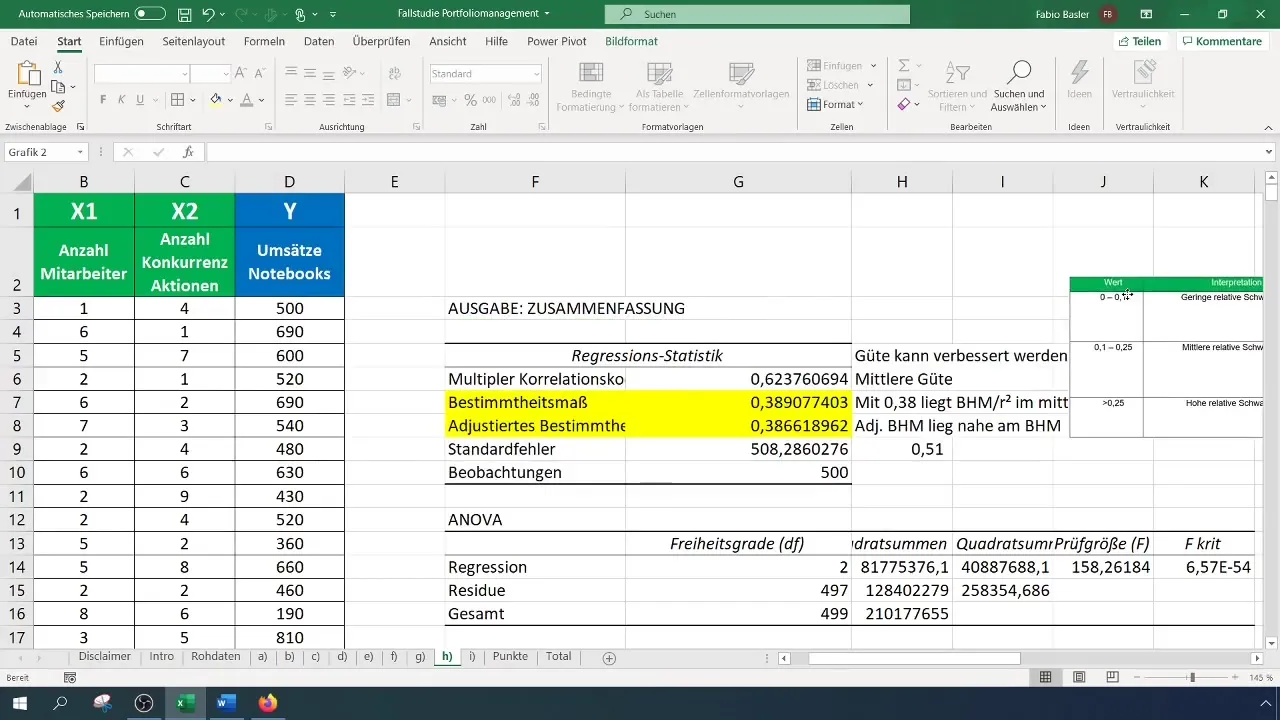
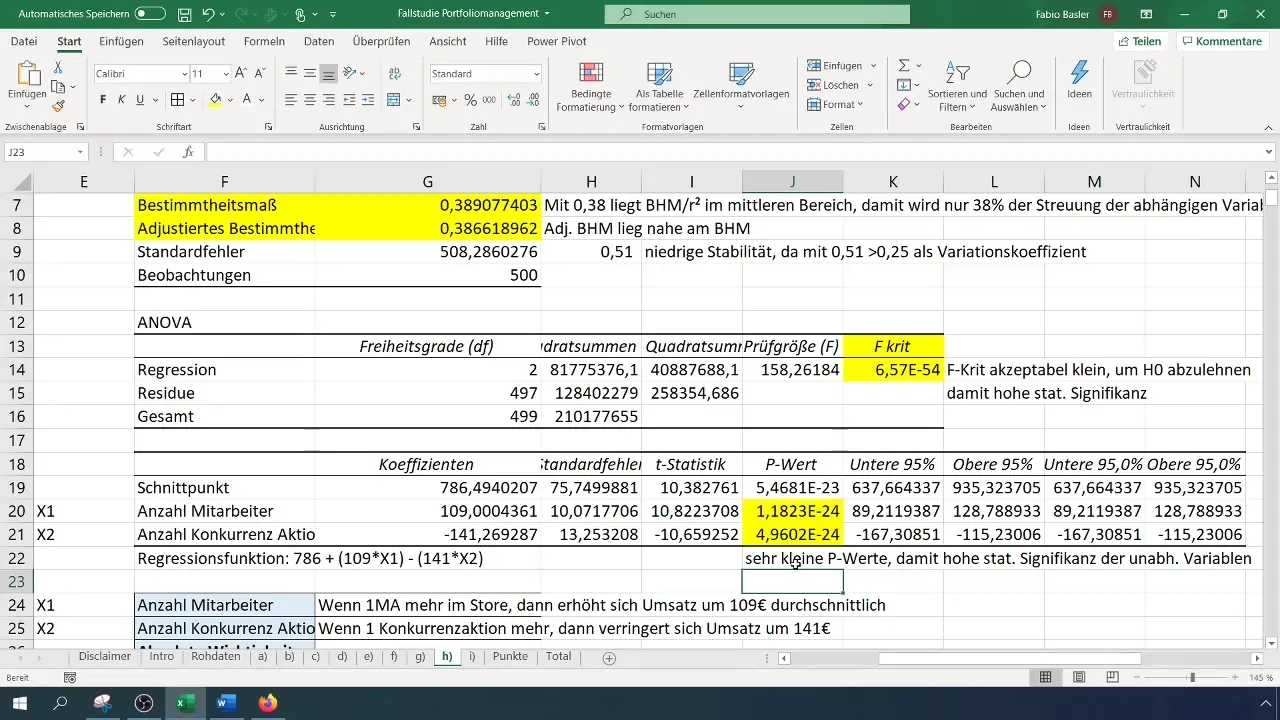
После проведения регрессионного анализа вы получите множество выводов и статистических данных. Первым важным пунктом является коэффициент детерминации (R²), который описывает долю объяснения зависимой переменной независимыми переменными. Значение R² равное 0,38 указывает на то, что 38% изменчивости в выручке могут быть объяснены этими двумя независимыми переменными.
В оценке важно обратить внимание на то, насколько стабильна модель. Вы можете использовать стандартную ошибку для определения стабильности. Например, если вы получаете стандартную ошибку 0,51, это означает высокую относительную изменчивость и низкую стабильность.
Оценка сильных факторов влияния
Определяющим этапом является выяснение, какая из независимых переменных оказывает более сильное влияние на зависимую переменную. Вы можете сделать это с помощью коэффициентов, указывающих абсолютную значимость переменных. Так, коэффициент x1 (количество сотрудников) равен 109, в то время как коэффициент x2 (количество конкурентных действий) равен -141. Это говорит о том, что каждое увеличение количества сотрудников увеличивает выручку на 109 евро, а каждое увеличение конкурентных действий уменьшает выручку на 141 евро.
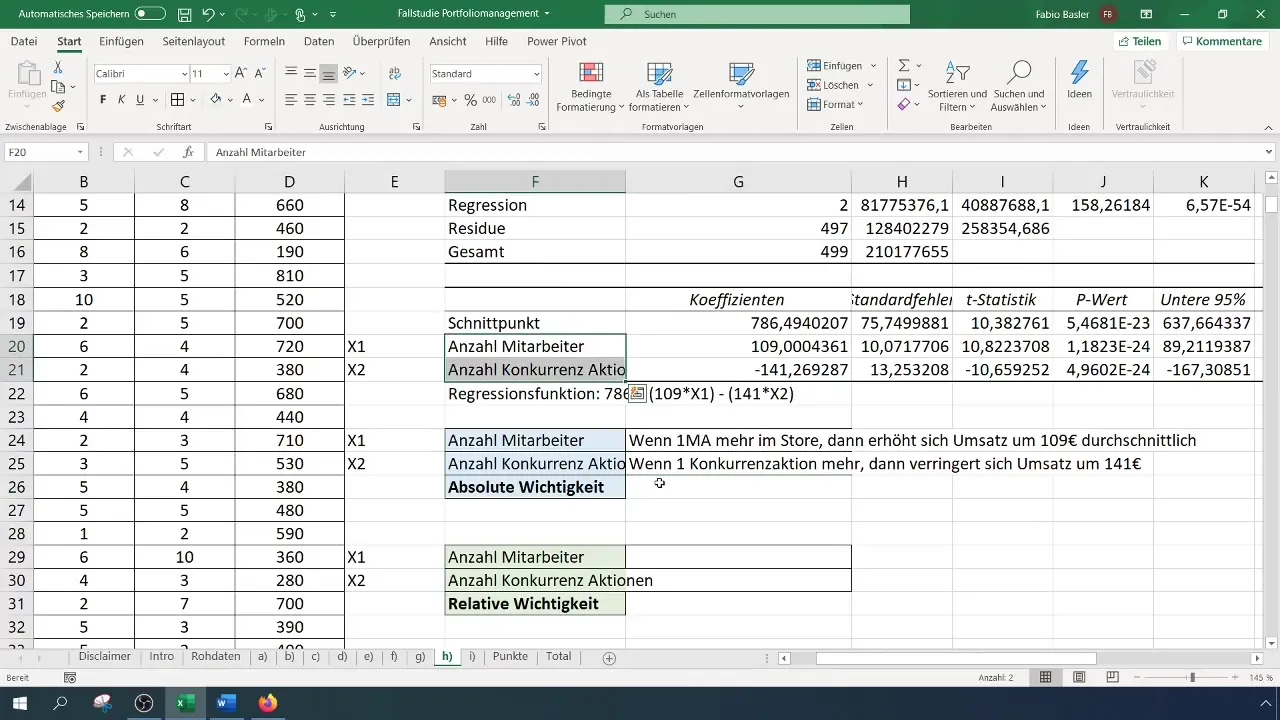
Оценка статистической значимости
Еще одним важным аспектом регрессионного анализа является статистическая значимость. Вы можете определить это по значениям p-значений и F-теста, которые оба должны иметь очень маленькие значения. Это говорит о том, что независимые переменные имеют значительное влияние на зависимую переменную и оправдывает использование модели.
Итог
Регрессионный анализ в Excel позволяет количественно оценить связь между различными переменными. В этом руководстве вы узнали шаги по выполнению и интерпретации множественной регрессии. Обратите внимание на качество и стабильность модели, а также критически оцените отдельные факторы влияния, чтобы принимать обоснованные решения в управлении портфелем.
Часто задаваемые вопросы
Какие данные мне нужны для регрессионного анализа?Вам понадобится зависимая переменная (например, выручка) и как минимум одна или несколько независимых переменных (например, количество сотрудников, действия конкурентов).
Как интерпретировать коэффициент детерминации R²?Более высокое значение R² означает, что большая часть изменчивости зависимой переменной объясняется независимыми переменными.
Как проверить статистическую значимость?Вы можете использовать p-значения и F-тест; низкие значения указывают на высокую значимость.
В чем разница между R² и скорректированным R²?Скорректированный R² учитывает количество независимых переменных и предоставляет более реалистичную оценку при моделях с несколькими переменными.
Как оценить силу факторов влияния?Это делается путем рассмотрения коэффициентов независимых переменных, которые количественно характеризуют влияние каждой переменной на зависимую переменную.


