Умение использовать инструменты анализа данных в Excel имеет решающее значение для успеха в бизнесе и продажах. Это руководство посвящено корреляционному и регрессионному анализу , чтобы выяснить, как количество сотрудников и количество телефонных звонков влияют на показатели продаж. Выполнение обоих анализов поможет вам оценить эти взаимосвязи количественно и сделать интерпретацию результатов понятной.
Ключевые выводы
- Разница между корреляцией и регрессией: корреляция показывает связь между двумя переменными, а регрессия анализирует влияние нескольких независимых переменных на зависимую переменную.
- Понимание статистической значимости и качества модели.
- Количественная оценка важности регрессоров.
Пошаговое руководство
1. подготовка к анализу данных
Прежде чем приступить к анализу, необходимо убедиться, что данные правильно подготовлены в Excel. Импортируйте данные о продажах, количестве сотрудников и телефонных звонках в рабочий лист Excel. Убедитесь, что все наборы данных полны и что имеются необходимые переменные.

2 Выполните корреляционный анализ
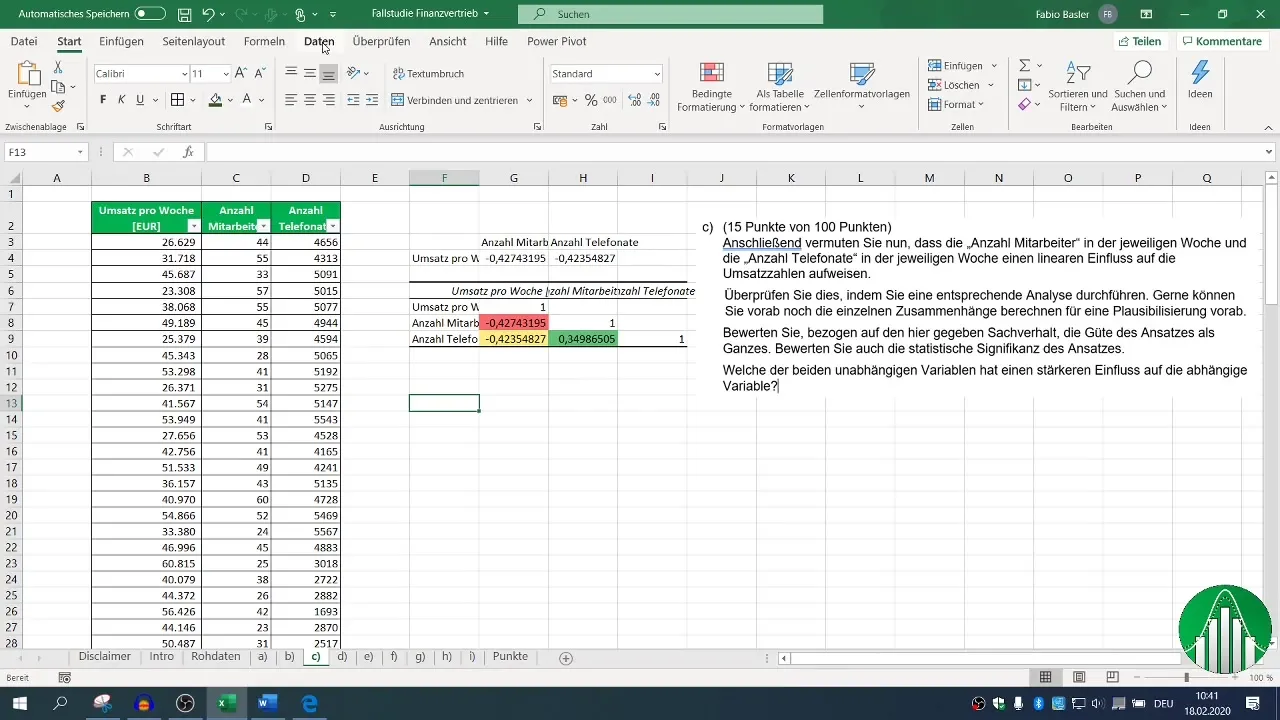
Чтобы проанализировать корреляцию между переменными оборота, количества сотрудников и телефонных звонков, можно рассчитать коэффициент корреляции. Для этого используйте формулу =КОРРЕЛ() в Excel. Чтобы получить представление обо всех переменных, создайте корреляционную матрицу.
Сначала выделите соответствующие столбцы для оборота и количества сотрудников. Используйте формулу =CORREL(, чтобы выбрать диапазоны для оборота и количества сотрудников. Результат показывает, насколько сильна корреляция.
3. создание корреляционной матрицы
Для более полного анализа мы рекомендуем использовать функции анализа данных Excel. Активируйте функцию анализа данных, если вы еще не сделали этого. Перейдите на вкладку "Данные", нажмите на "Анализ данных" и выберите "Корреляция".
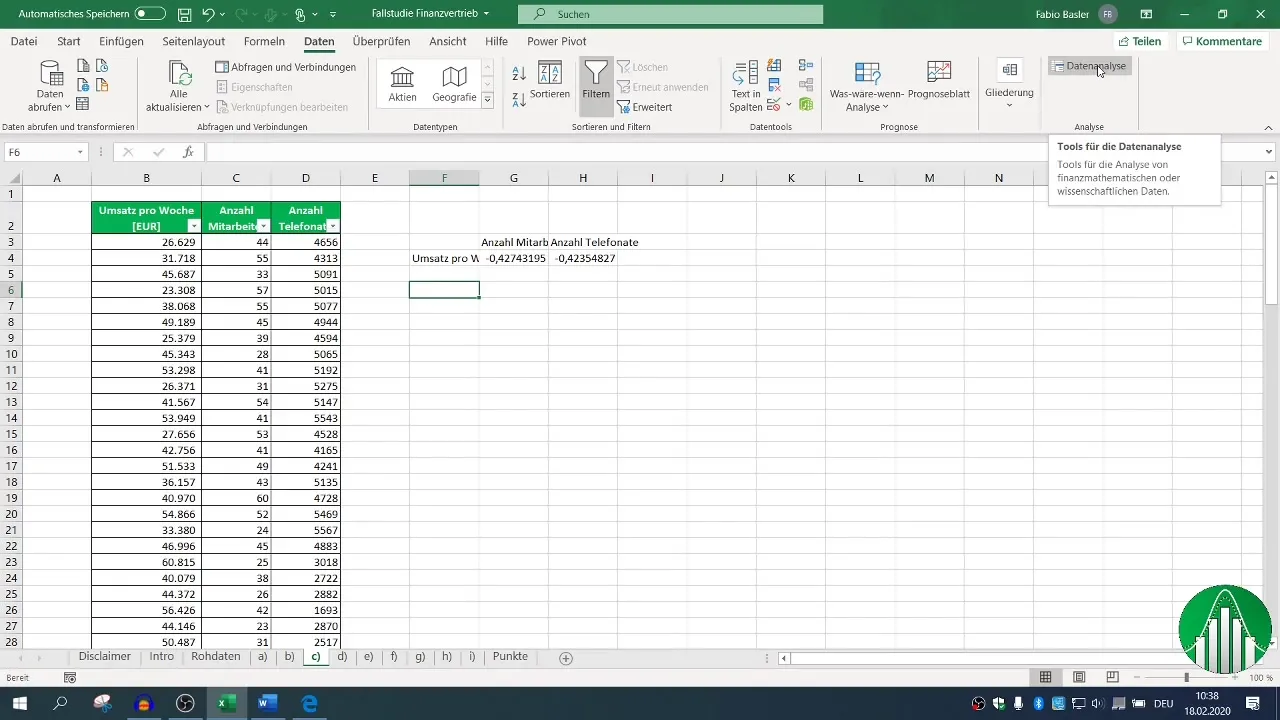
Определите диапазон ввода данных и установите флажок для заголовка, чтобы Excel правильно распознал метки. Определив выходной диапазон, вы можете сгенерировать корреляционную матрицу, которая покажет вам все соответствующие взаимосвязи.
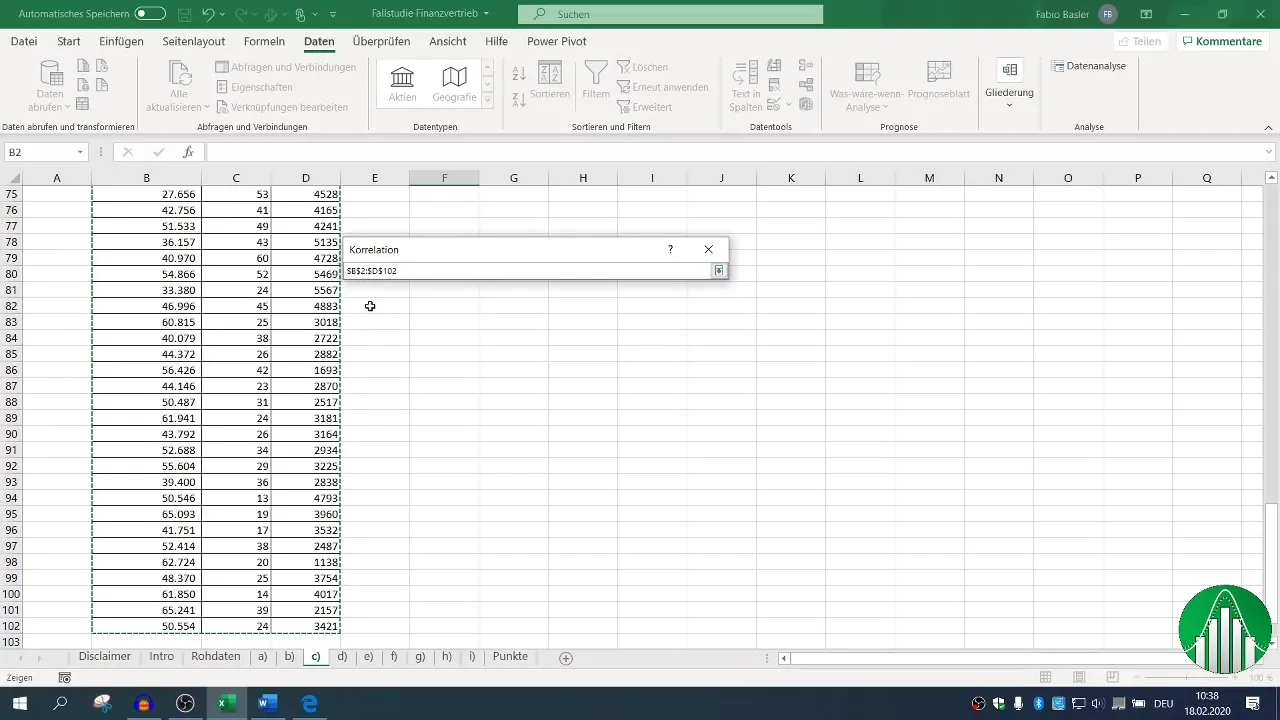
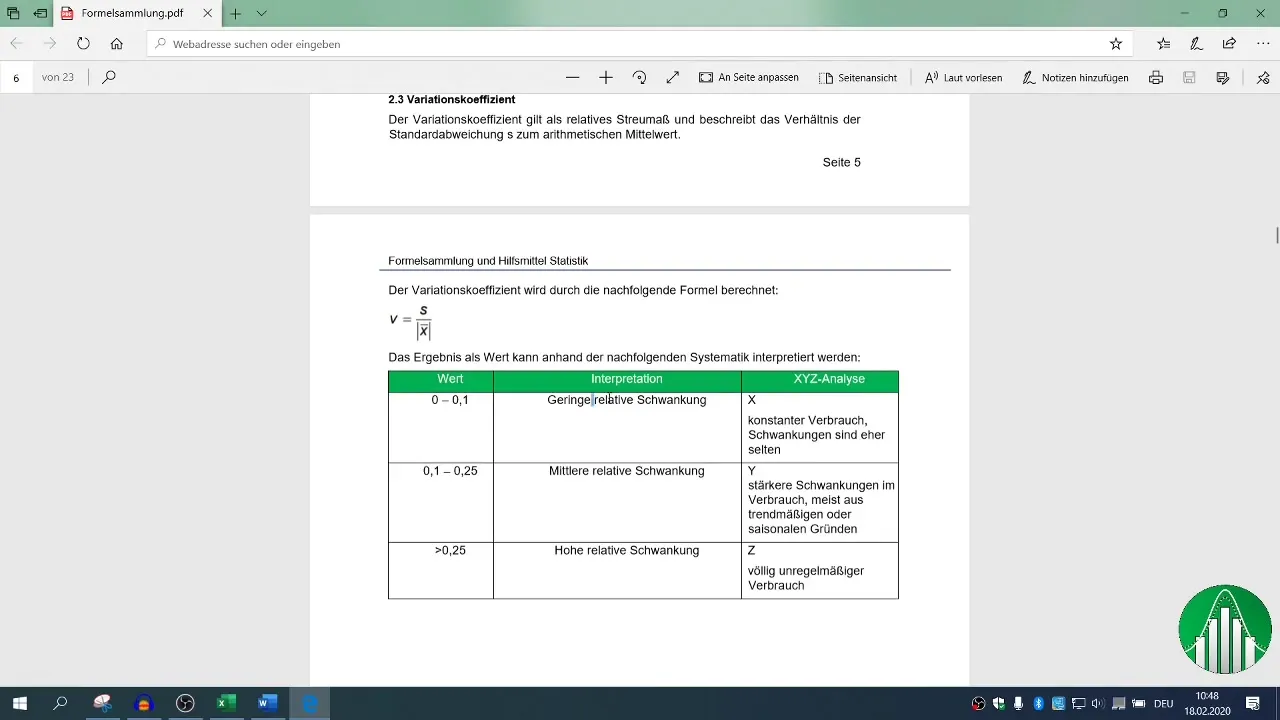
4. Визуализация корреляций
Чтобы сделать результаты более наглядными, полезно использовать графическое представление с помощью диаграммы XY. Выберите данные по осям X и Y и сгенерируйте облако точек.
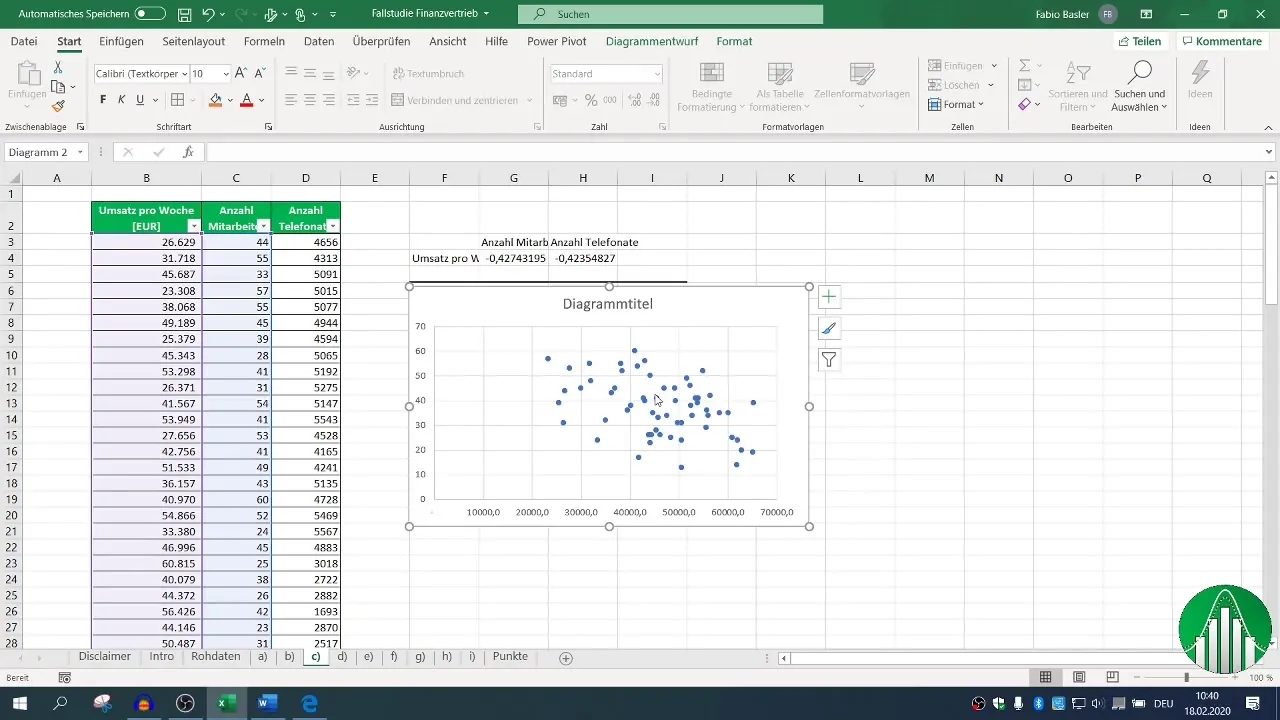
Добавьте линию тренда для визуализации взаимосвязи. Это может дать более интуитивное представление о данных.
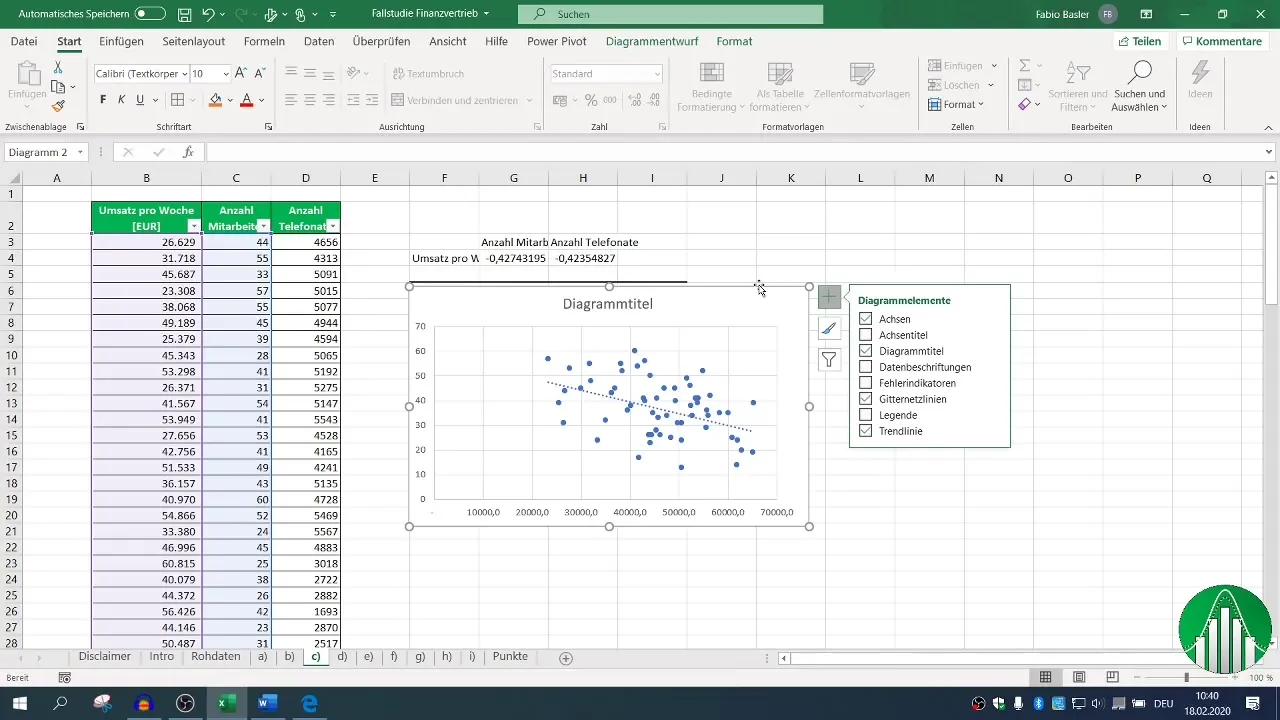
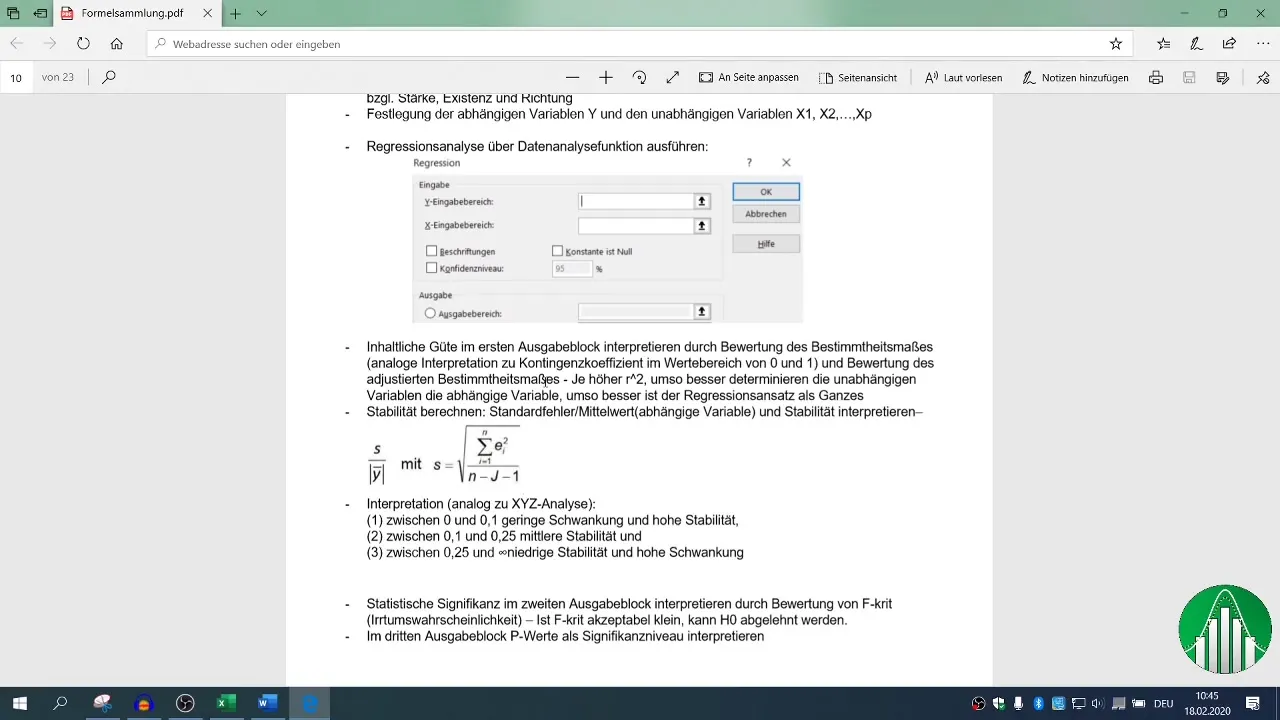
5. Проведение регрессионного анализа
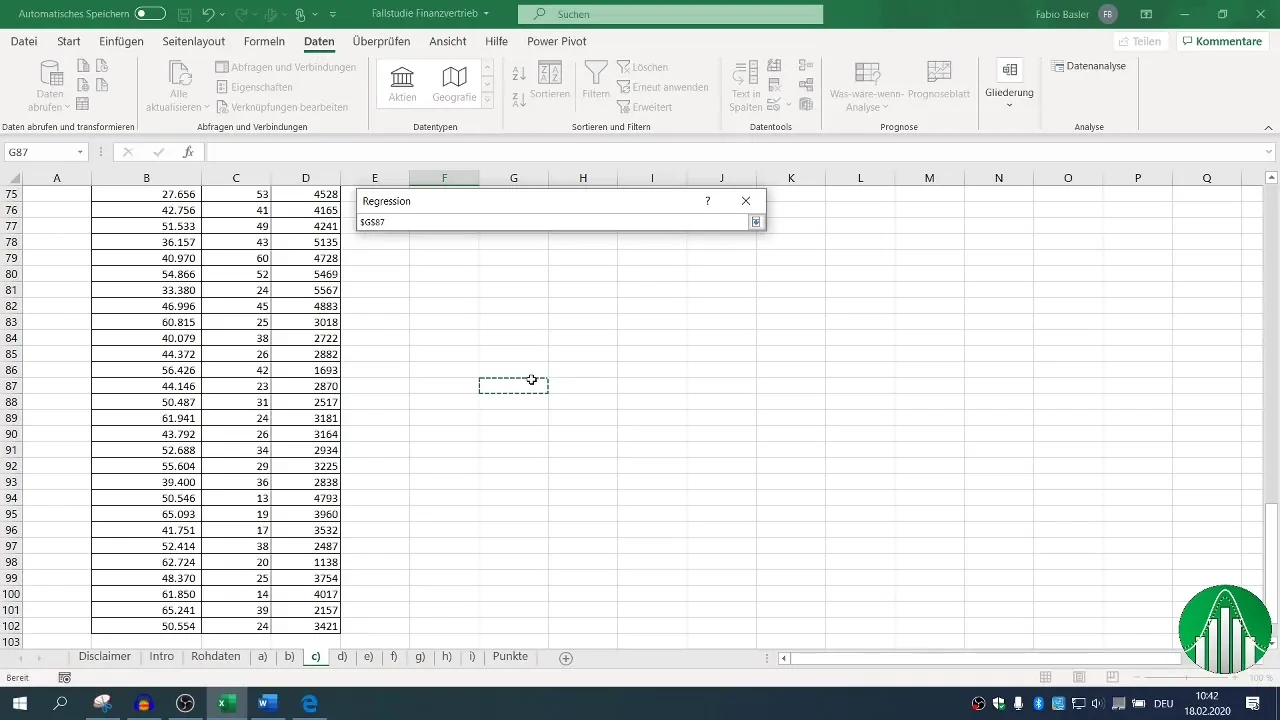
Теперь наступает этап регрессионного анализа. Снова перейдите в раздел "Данные" и выберите "Анализ данных", затем "Регрессия". Здесь вы можете определить зависимую переменную (оборот) и независимые переменные (количество сотрудников и телефонных звонков) для области ввода.
Убедитесь, что установлен заголовок для значений, и определите выходной диапазон. По умолчанию уровень доверия установлен на 95 %, что достаточно для большинства анализов.
6. оценка регрессионного анализа
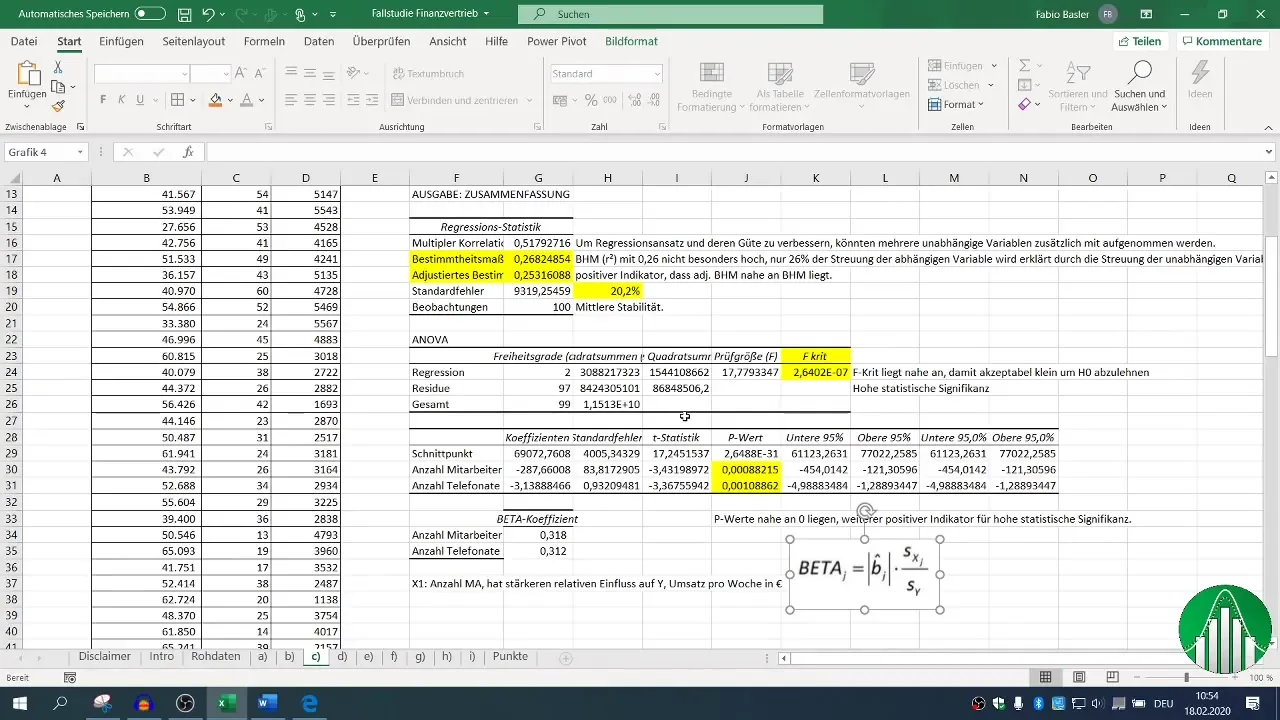
После проведения регрессии в вашем распоряжении окажутся различные блоки вывода. Сконцентрируйтесь на коэффициенте детерминации (R²), который описывает качество модели. R², равный 0,26, означает, что только 26 % изменчивости продаж объясняется независимыми переменными.
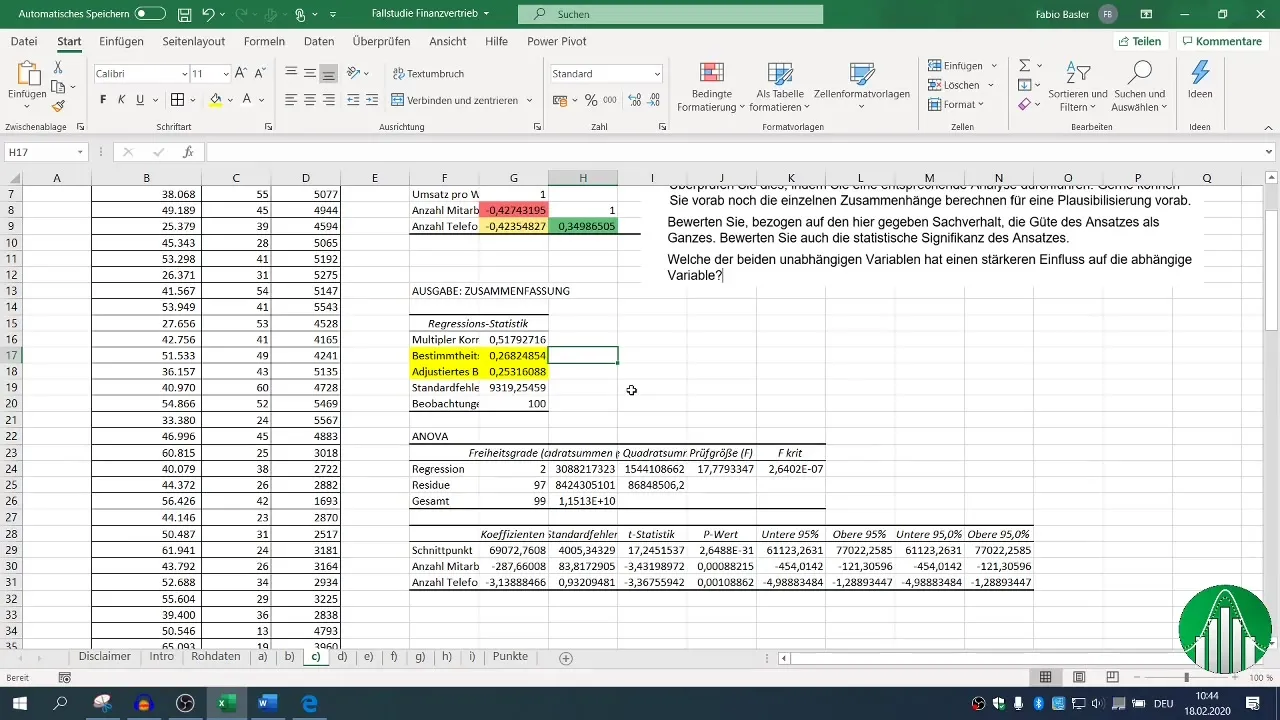
Скорректированный коэффициент детерминации должен быть близок к R², что в данном случае является положительным показателем.
7 Оценка статистической значимости
F-значение и p-значения независимых переменных имеют решающее значение для оценки статистической значимости вашей модели. Значение p-value ниже 0,05 указывает на то, что связь статистически значима.
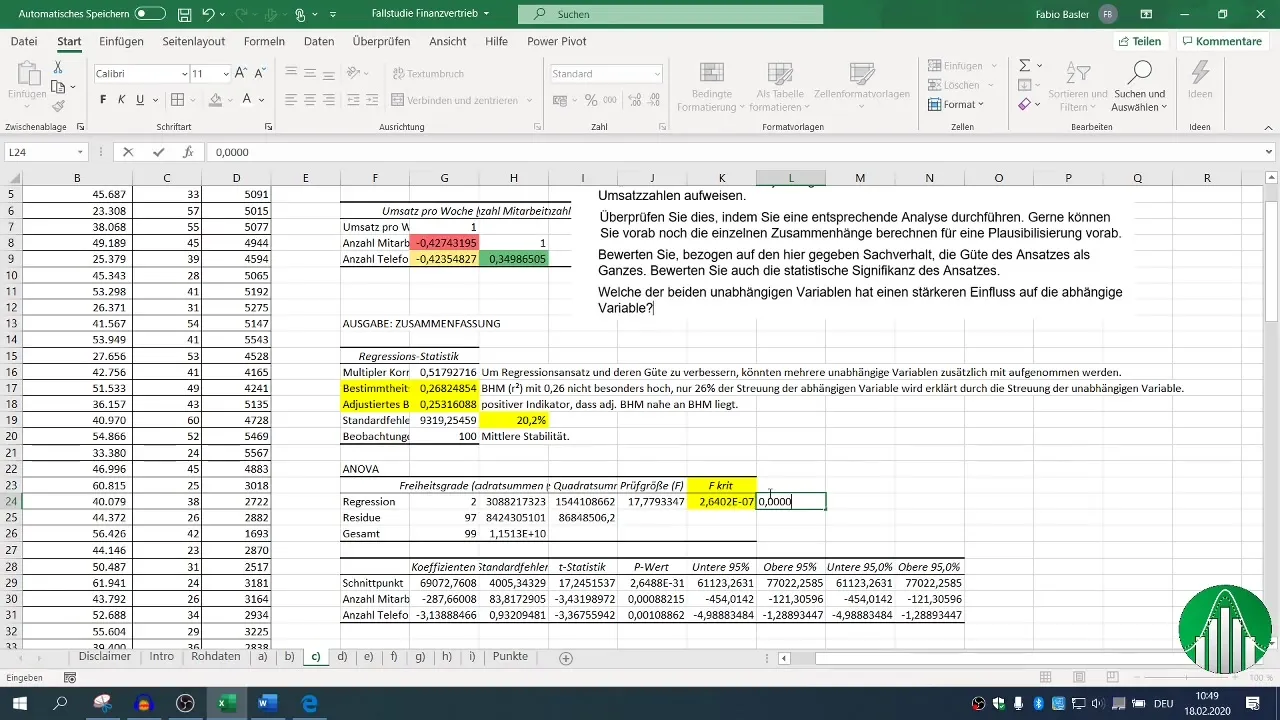
Оценка этих статистических параметров в сочетании с R² поможет вам понять стабильность и значимость результатов.
8 Сравнение влияющих факторов
В конечном итоге вас интересует, какой фактор - количество сотрудников или телефонных звонков - оказывает более сильное влияние на показатели продаж. Здесь вы берете бета-коэффициенты и сравниваете их.
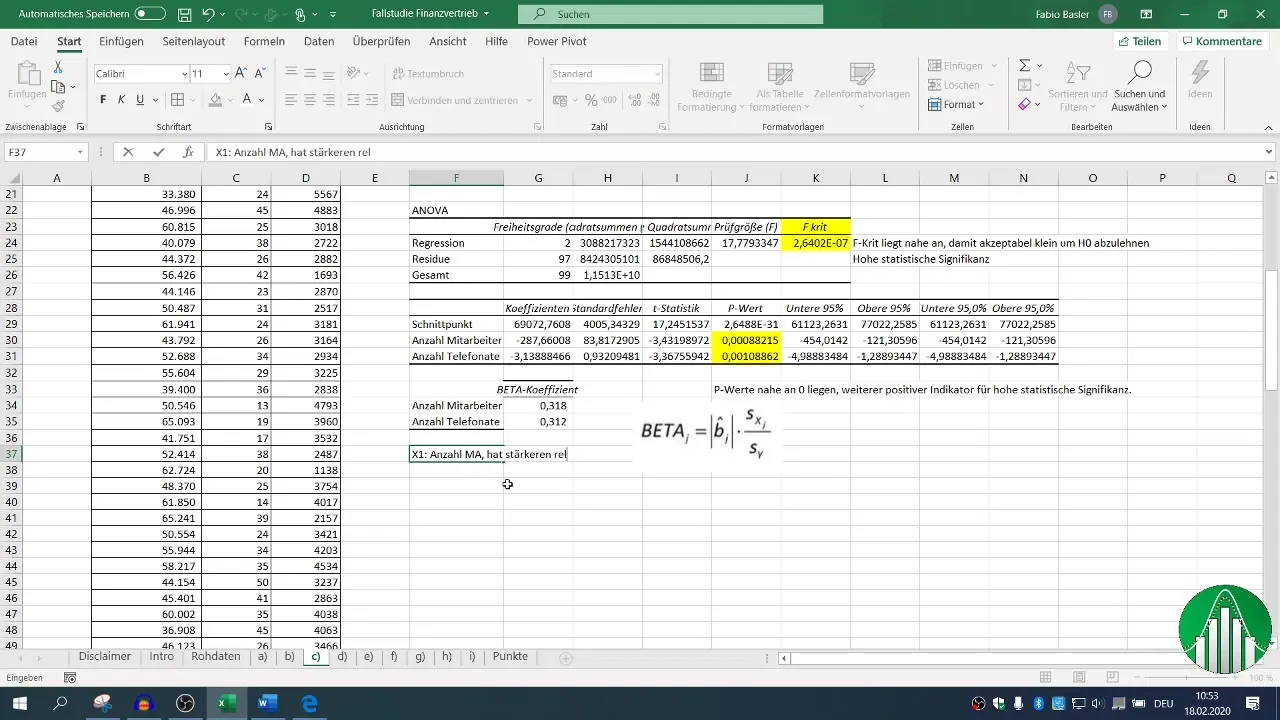
Более высокий бета-коэффициент указывает на относительное влияние; может оказаться, что количество сотрудников оказывает большее влияние на оборот, чем количество телефонных звонков.
Резюме
Предыдущий анализ дал вам ценные сведения о статистических взаимосвязях между переменными оборота, количества сотрудников и телефонных звонков. Систематически выполняя корреляционный и регрессионный анализ в Excel, вы сможете принимать обоснованные решения на основе полученных результатов.
Часто задаваемые вопросы
Почему корреляционный анализ важен?Корреляционный анализ помогает выявить взаимосвязь между двумя переменными до проведения подробного регрессионного анализа.
Как интерпретировать R² в регрессионном анализе?R² 0,26 означает, что 26 % вариации зависимой переменной (продаж) объясняется независимыми переменными.
В чем разница между корреляцией и регрессией?Корреляция измеряет связь между двумя переменными, а регрессия оценивает влияние нескольких независимых переменных на зависимую переменную.
Как проверить статистическую значимость?Статистическая значимость проверяется с помощью p-значения; p-значения ниже 0,05 считаются значимыми.
Какую роль играют бета-коэффициенты? Бета-коэффициенты показывают относительное влияние независимых переменных на зависимую переменную.


