Проверка статистических гипотез - незаменимый инструмент для принятия обоснованных решений. В следующем разделе мы покажем вам, как выполнить двухвыборочный F-тест в Excel для проверки достоверности гипотез о дисперсии данных о продажах. В этом руководстве вы шаг за шагом пройдете весь процесс, чтобы уверенно применять изученные методики.
Основные выводы
- Двухвыборочный F-тест используется для сравнения дисперсий двух групп данных.
- Цель - проверить, отличается ли дисперсия фактических данных о продажах от предполагаемого значения.
- Excel предоставляет инструменты для выполнения необходимых расчетов и сравнений.
Пошаговые инструкции
1. подготовка данных
Прежде чем приступить к тестированию, убедитесь, что ваши данные подготовлены. Важно снять фильтры, чтобы включить все необходимые данные. Начните с выбора данных в соответствующих столбцах.

2. определение параметров
Определите параметры теста. Вы должны знать, сколько точек данных вы анализируете. В нашем примере мы предполагаем, что у вас есть 100 данных о продажах, которые имеют нормальное распределение.

3. Запись предыдущего значения дисперсии
Известная дисперсия или значение продаж в прошлом играет центральную роль в вашем анализе. В данном примере предыдущее значение составляет 116 миллионов евро в неделю.
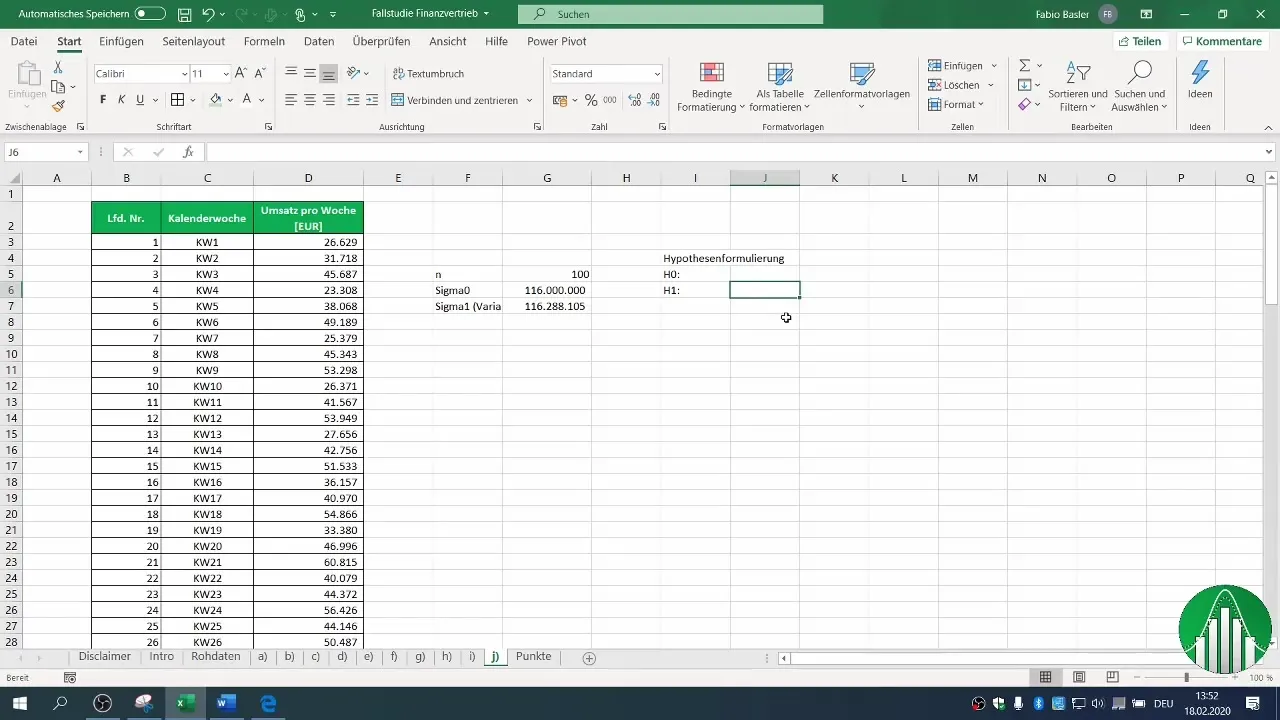
4. Формулировка гипотезы
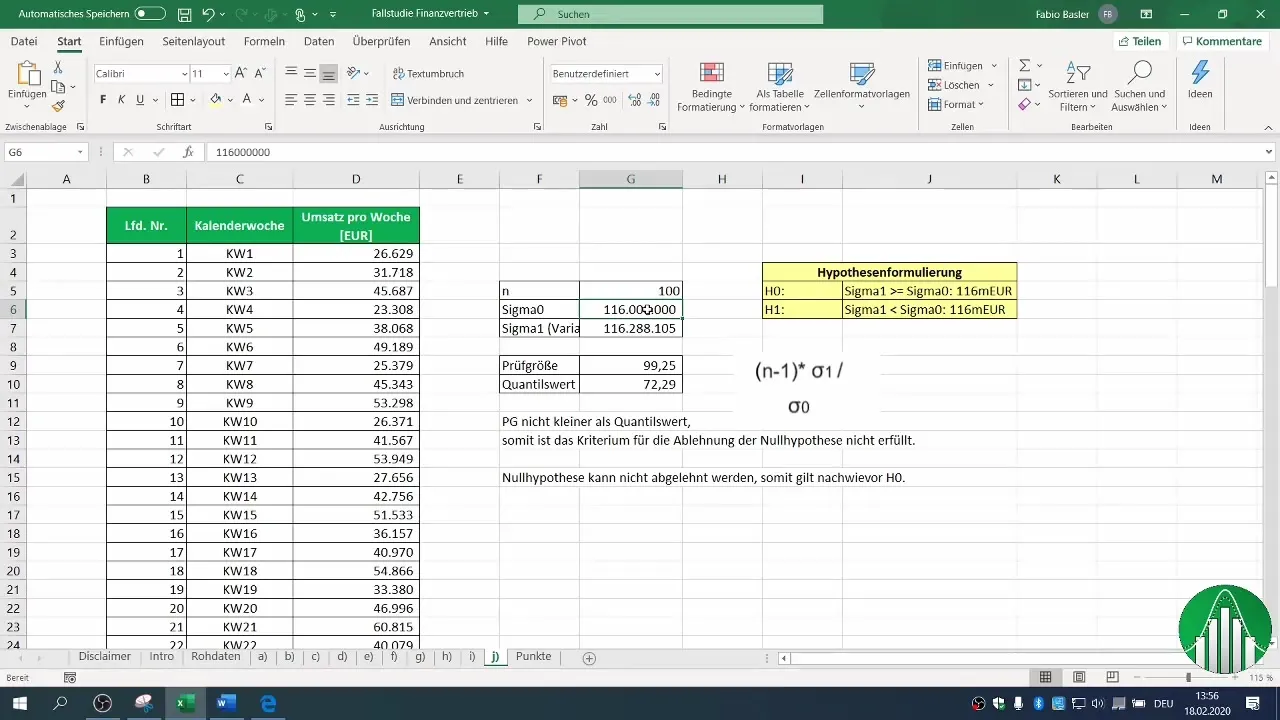
Сформулируйте нулевую гипотезу (H0) и альтернативную гипотезу (H1). В данном случае H0 заключается в том, что дисперсия осталась прежней или больше 116 миллионов, а H1 предполагает, что дисперсия уменьшилась.
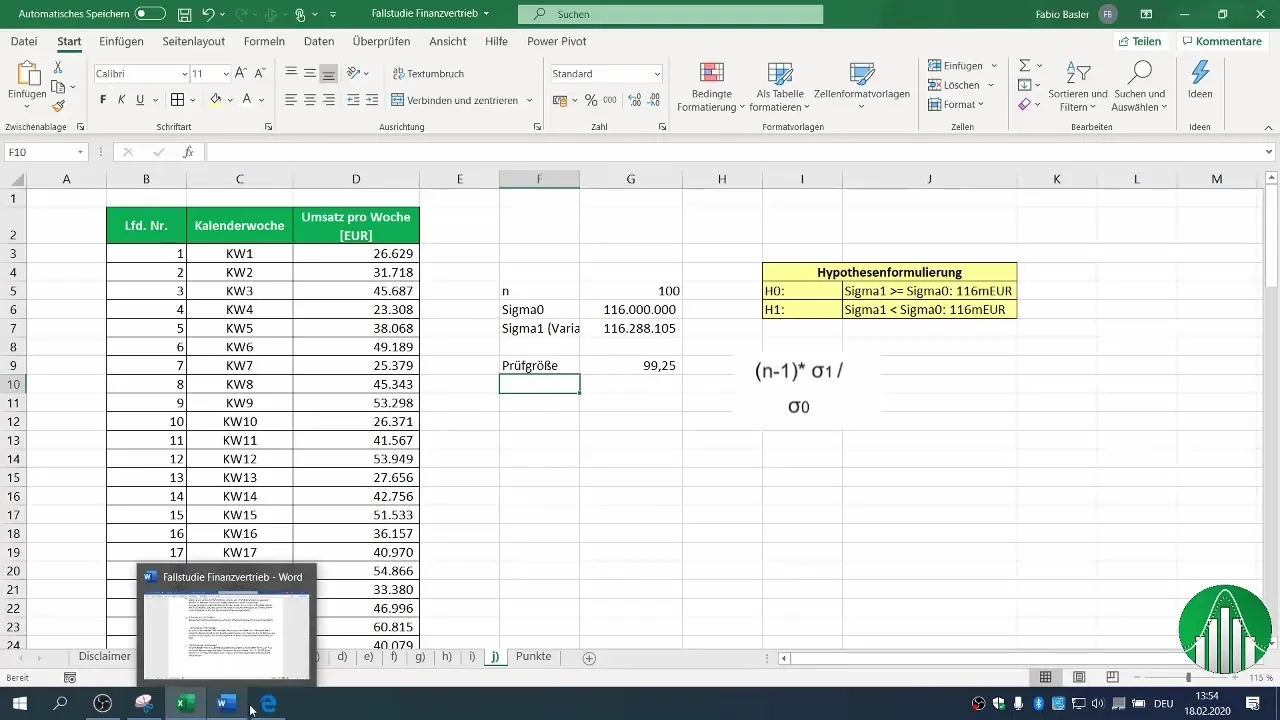
5. Расчет тестовой статистики
Вы можете рассчитать тестовую статистику, используя дисперсию вашей выборки. Выполните необходимые вычисления, чтобы определить значение тестовой статистики. Оно определяется по формуле (n-1) * σ1 / σ0, где σ1 - дисперсия вашей выборки, а σ0 - дисперсия прошлого.
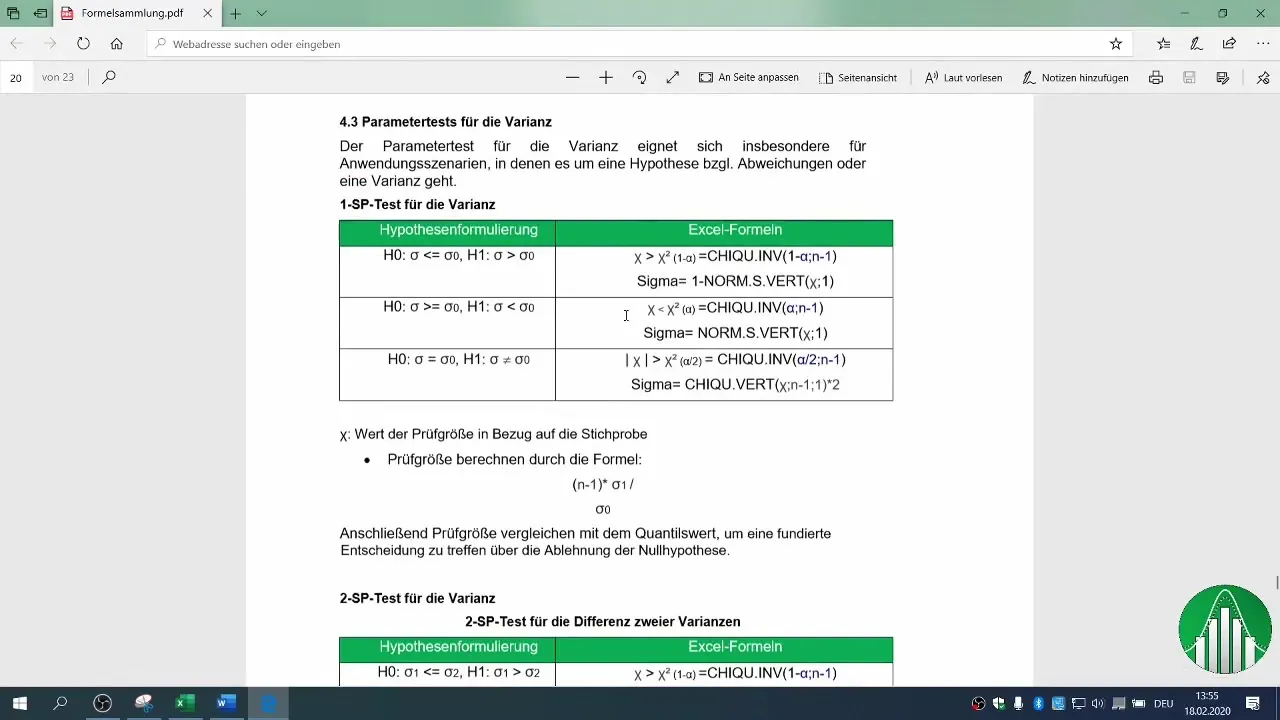
6. определение критического диапазона
Чтобы решить, можно ли отвергнуть нулевую гипотезу, необходимо определить критический интервал. Используйте таблицу распределения хи-квадрат для определения уровня доверия. В нашем примере мы использовали вероятность ошибки в 2 %.
7. сравнение тестовой и критической переменной
Теперь проверьте, меньше ли рассчитанная вами тестовая статистика критического значения. В данном случае мы обнаружили, что наша тестовая статистика не меньше критического значения квантиля.
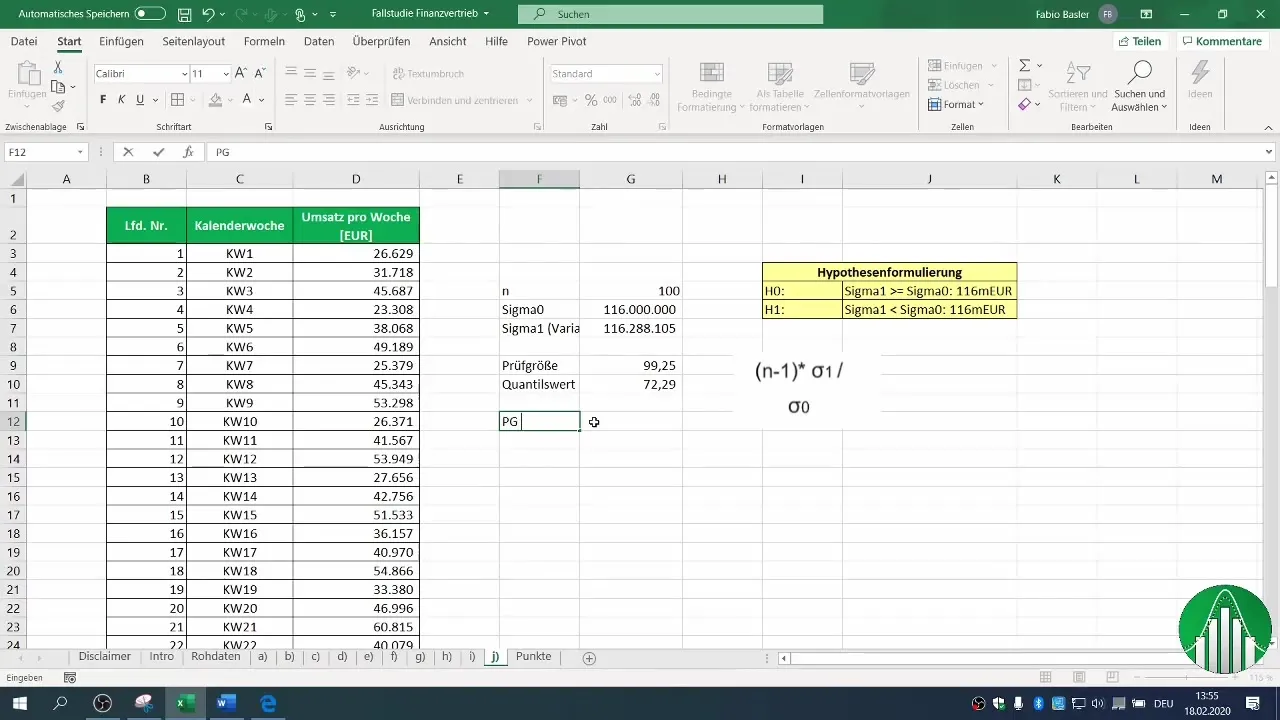
8. Сделайте вывод
На основе проведенного сравнения вы можете решить, можно ли отвергнуть нулевую гипотезу или нет. В нашем примере мы определили, что нулевая гипотеза не может быть отвергнута. Это означает, что дисперсия ваших данных о продажах по-прежнему соответствует предполагаемому значению или даже больше.
Резюме
В этом руководстве мы подробно рассмотрели, как выполнить двухвыборочный F-тест в Excel. Вы узнали, как подготовить данные, сформулировать гипотезы, рассчитать статистику теста, определить критический диапазон и, наконец, сделать выводы. Выполнив эти шаги, вы сможете самостоятельно проводить статистический анализ.
Часто задаваемые вопросы
Что такое двухвыборочный F-тест? Двухвыборочный F-тест используется для сравнения дисперсий двух групп данных.
Как сформулировать гипотезы для F-теста? Нулевая гипотеза утверждает, что дисперсия равна или больше, а альтернативная гипотеза предполагает ее уменьшение.
Как найти критическое значение для теста?Критическое значение можно вывести с помощью таблиц хи-квадрат, основываясь на доверительном уровне и степенях свободы.
Что делать, если нулевая гипотеза не может быть отвергнута?Это означает, что данные соответствуют предполагаемому значению дисперсии или даже демонстрируют большие колебания.
Нужно ли мне специальное программное обеспечение для проведения теста?Для проведения двухвыборочного F-теста достаточно Excel, если данные подготовлены.

