Анализ ранговой корреляции занимает центральное место в статистическом анализе взаимосвязей между переменными. Особенно когда речь идет о данных с порядковой шкалой, ранговая корреляция Спирмена является ценным методом для выявления закономерностей и связей. В этом пошаговом руководстве вы узнаете, как рассчитать ранговую корреляцию Спирмена для опроса с помощью Excel.
Ключевые выводы
- Ранговая корреляция измеряет силу и направление монотонной связи между двумя порядковыми переменными.
- Коэффициент ранговой корреляции Спирмена особенно полезен, когда одна из переменных является порядковой, а другая - метрической.
- Его можно рассчитать в Excel с помощью простых формул и функций.
Пошаговые инструкции
Сначала определите переменные, которые мы хотим проанализировать. В данном случае это удовлетворенность клиентов (порядковая шкала, значения 1-3) и количество заказов (метрическая шкала).
Чтобы создать рейтинг удовлетворенности и количества заказов, вам понадобится таблица с соответствующими данными. Убедитесь, что вы ввели эти данные в Excel.

После того как вы ввели данные в Excel, давайте посмотрим, как рассчитать ранговую корреляцию по Спирмену. Для этого мы используем функцию "Ранг.Среднее" в Excel, которая возвращает ранг числа в списке. Сначала мы используем формулу удовлетворения:
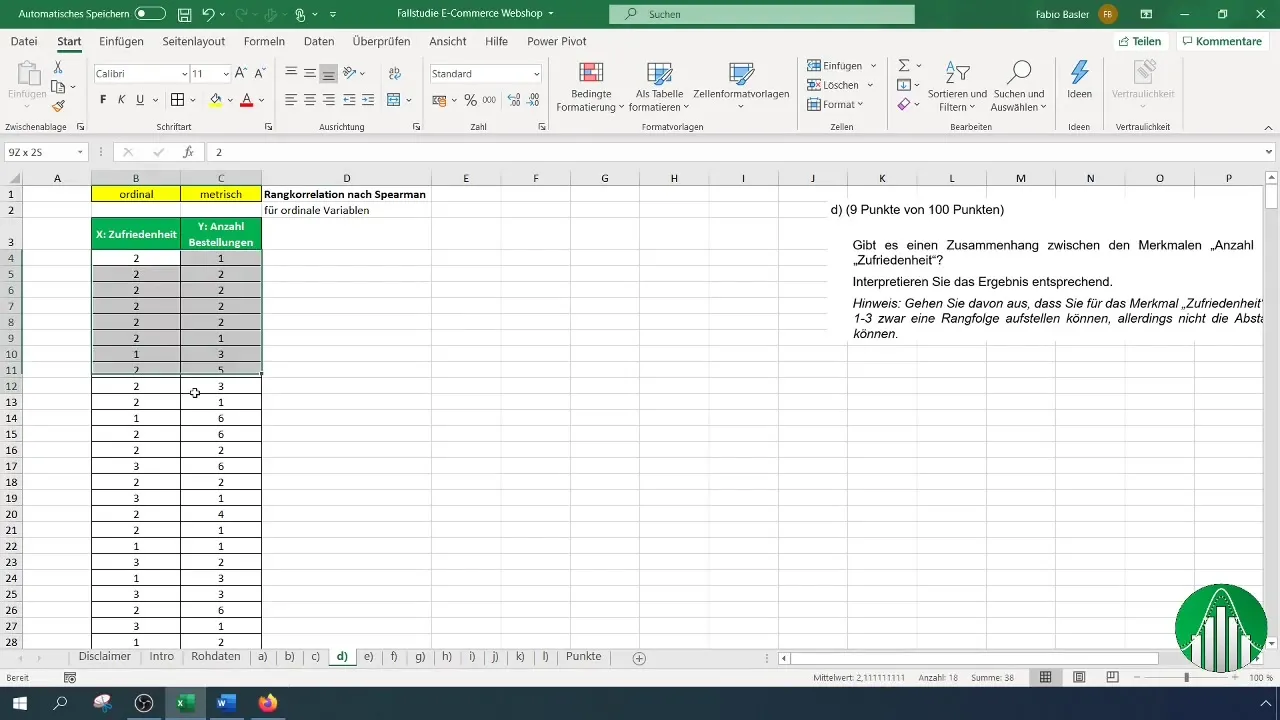
Применяя эту формулу, не забудьте выбрать столбец для удовлетворенности и указать весь диапазон от B4 до конца вашего ряда данных, чтобы правильно определить ранги.
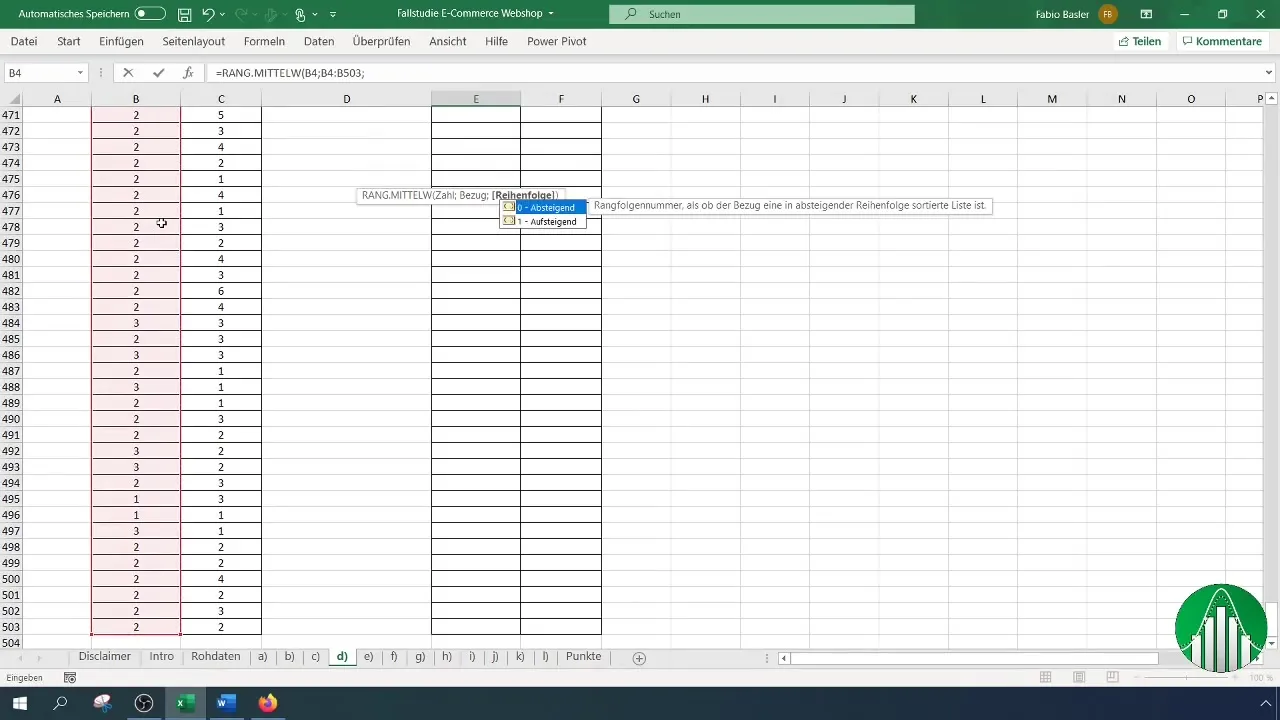
Определите, в каком порядке вы хотите отсортировать ранги - по возрастанию или по убыванию. Как правило, имеет смысл сортировать их по возрастанию. Подчеркните, что ссылки на ячейки для рангов фиксируются с помощью клавиши F4. Это важно для того, чтобы ссылки не изменились при копировании.
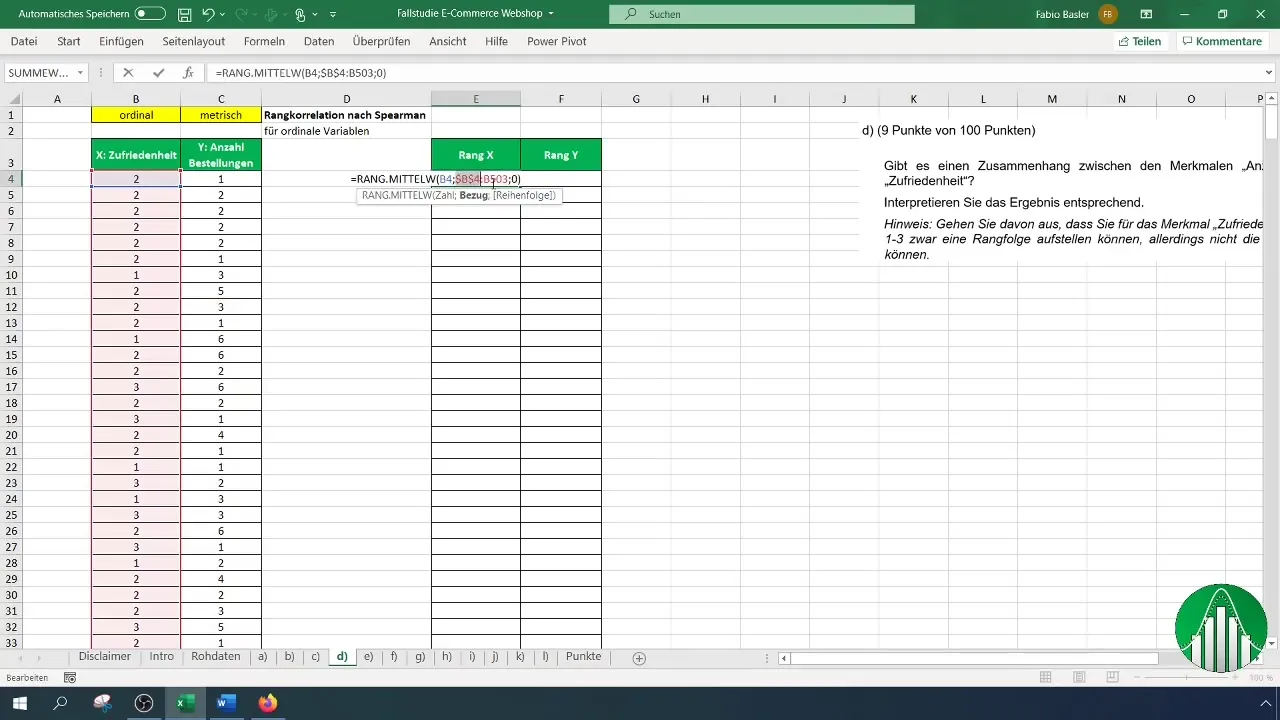
После того как вы установили ранги для удовлетворенности, повторите процесс для количества заказов. Убедитесь, что вы правильно применили формулу и ссылки.
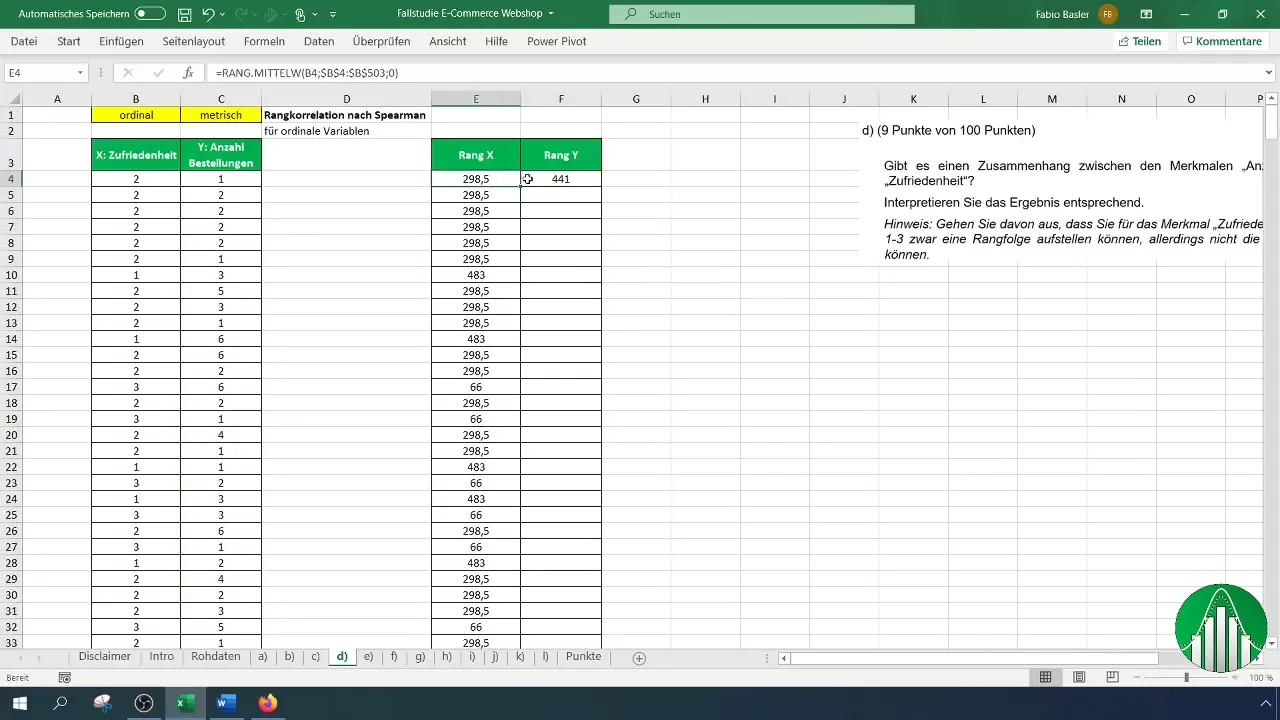
Получив оба ранжирования (удовлетворенность и количество заказов), вы можете рассчитать коэффициент ранговой корреляции Спирмена. Для этого используйте формулу "=CORREL" для определения взаимосвязи. Синтаксис формулы следующий:
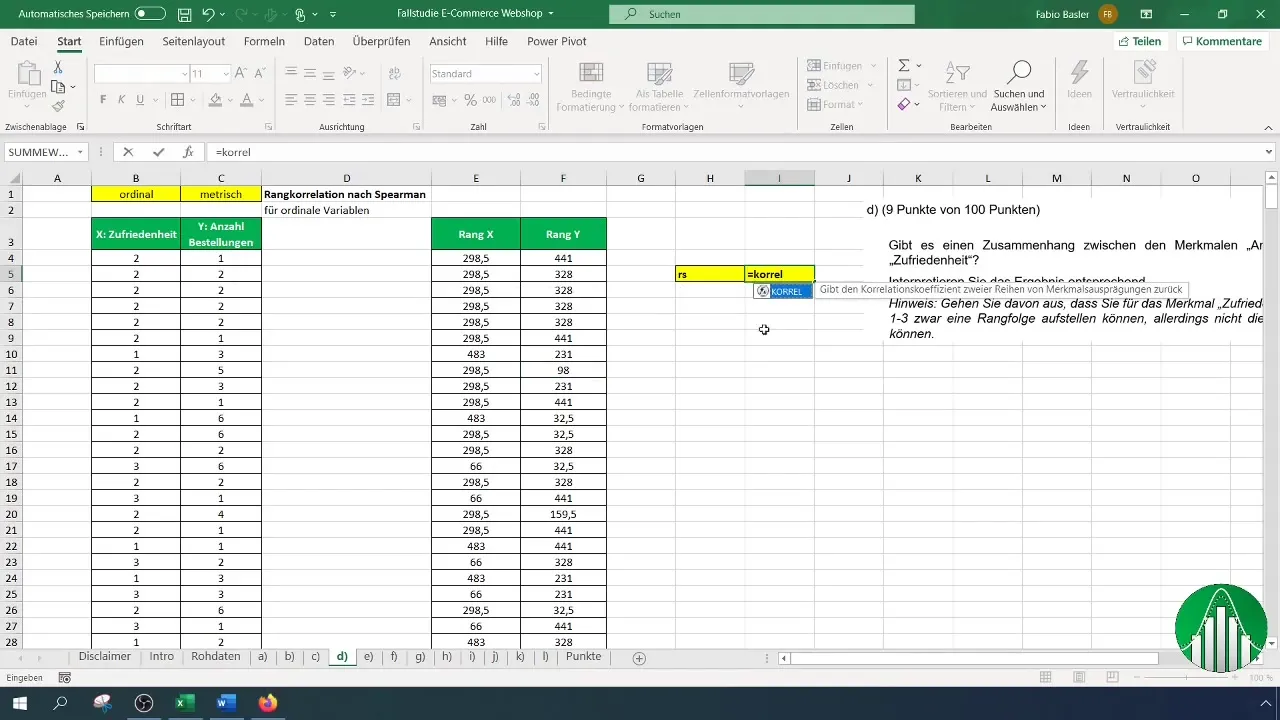
Введите ранговый список удовлетворенности для первой ссылки и ранговый список заказов для второй. Теперь Excel автоматически рассчитает коэффициент ранговой корреляции Спирмена.

Каков результат вашего расчета? Значение 5,61 % указывает на слабую положительную корреляцию между удовлетворенностью и количеством заказов. Это означает, что между этими двумя переменными практически нет значимой связи.
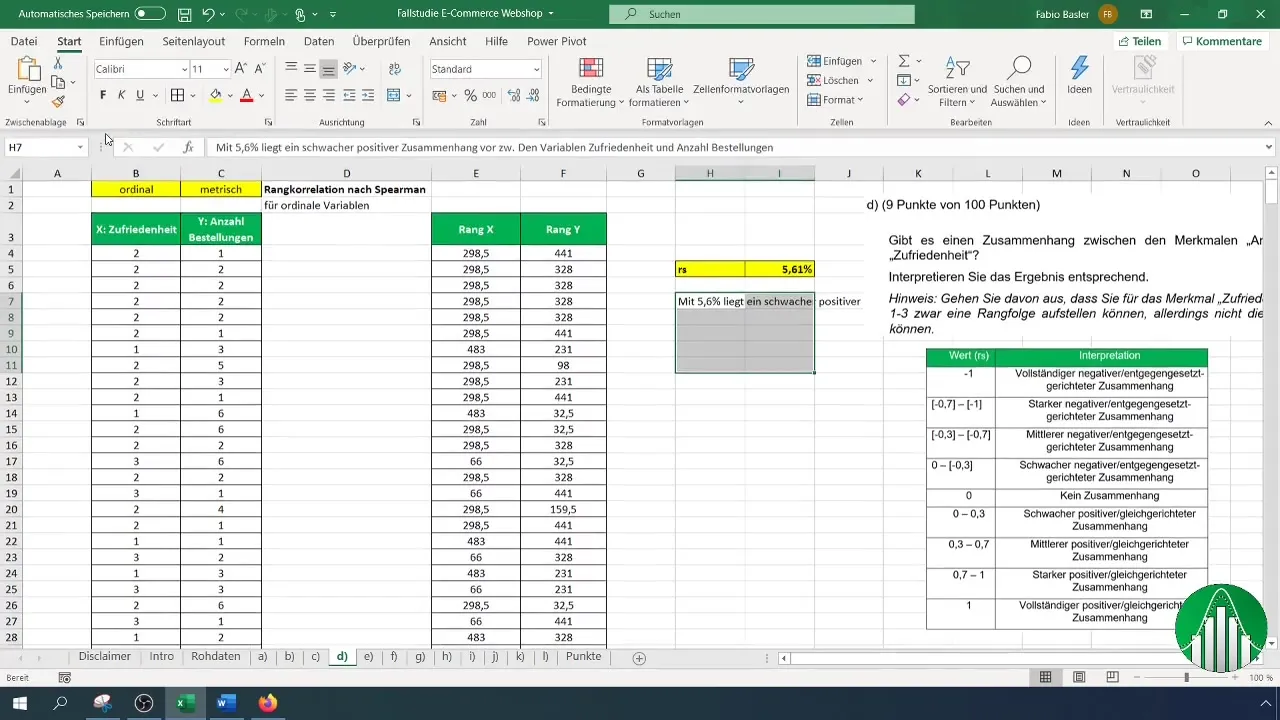
Чтобы интерпретировать результаты, используйте таблицу значений, показывающую различные области ранговой корреляции. После интерпретации мы подтверждаем, что низкий уровень корреляции означает, что переменные относительно независимы.
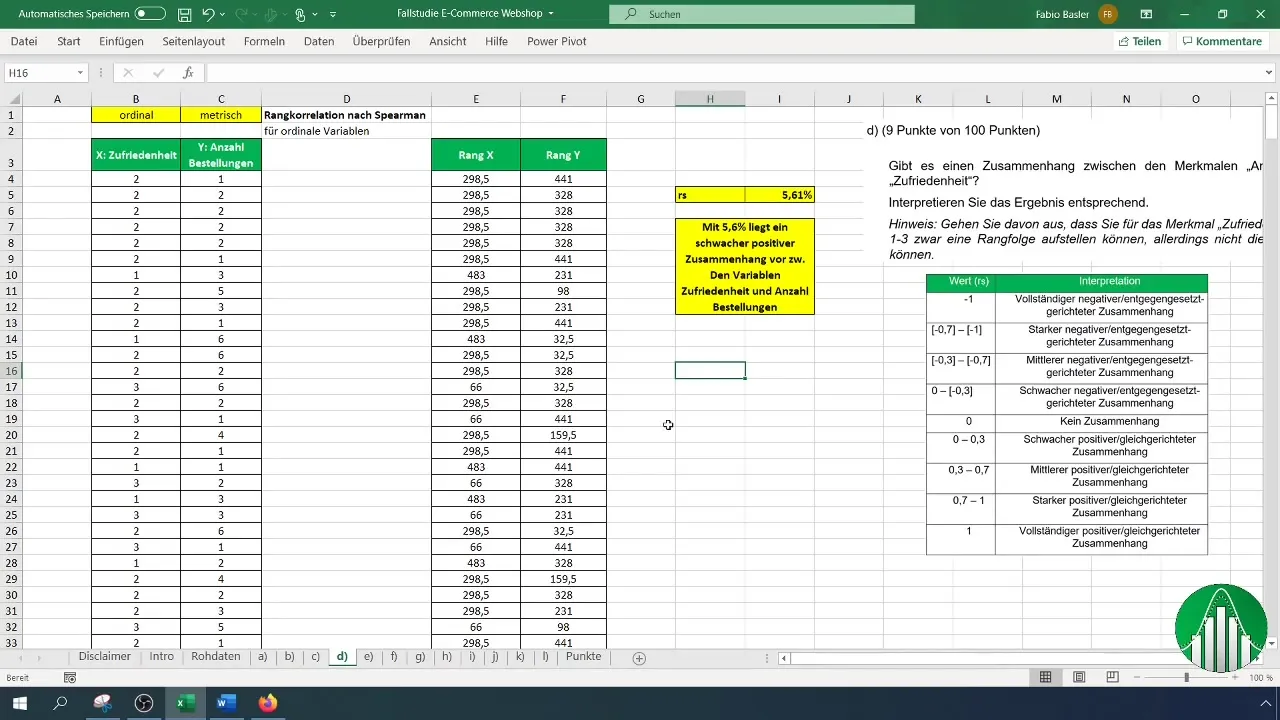
Резюме
Выполнение анализа ранговой корреляции Спирмена в Excel позволяет получить ценные сведения о взаимосвязях между порядковыми и метрическими переменными. Метод прост в использовании и дает четкое представление о любых корреляциях.
Часто задаваемые вопросы
Что такое коэффициент ранговой корреляции Спирмена? Коэффициент ранговой корреляции Спирмена измеряет силу и направление монотонной связи между двумя переменными.
Когда полезно использовать коэффициент Спирмена? Он полезен, когда хотя бы одна из переменных имеет порядковую шкалу.
Как рассчитать коэффициент Спирмена в Excel?Используйте функцию "rank.mean" для определения рангов, а затем функцию "KORREL" для расчета зависимости.
Каков диапазон значений коэффициента Спирмена? Коэффициент находится в диапазоне от -1 до 1. Значения, близкие к 1, указывают на сильную положительную корреляцию, а значения, близкие к -1, - на сильную отрицательную корреляцию.
Что может означать значение 5,61 % в ранговой корреляции? Значение 5,61 % указывает на слабую положительную корреляцию, что говорит о том, что переменные относительно независимы.


