Регрессионный анализ в Excel: Как анализировать данные

Регрессионный анализ - важнейший инструмент для анализа и количественной оценки взаимосвязей между различными переменными. В этом руководстве я покажу вам, как провести регрессионный анализ в Excel, чтобы смоделировать линейную функциональную зависимость между различными характеристиками успешности компании и ее оборотом. Нас особенно интересует, какие из характеристик оказывают наиболее сильное влияние на оборот. Пройдите этот процесс вместе со мной шаг за шагом.

Основные выводы

• Проведите регрессионный анализ в Excel для определения корреляций между переменными.
• Интерпретация качества регрессионного анализа с помощью коэффициента детерминации.
• Оценка статистической значимости с помощью p-значений и F-значений.
• Расчет относительной важности независимых переменных с помощью бета-коэффициента.

Пошаговые инструкции

Чтобы успешно выполнить регрессионный анализ в Excel, выполните следующие шаги:

Шаг 1: Подготовьте и вставьте данные

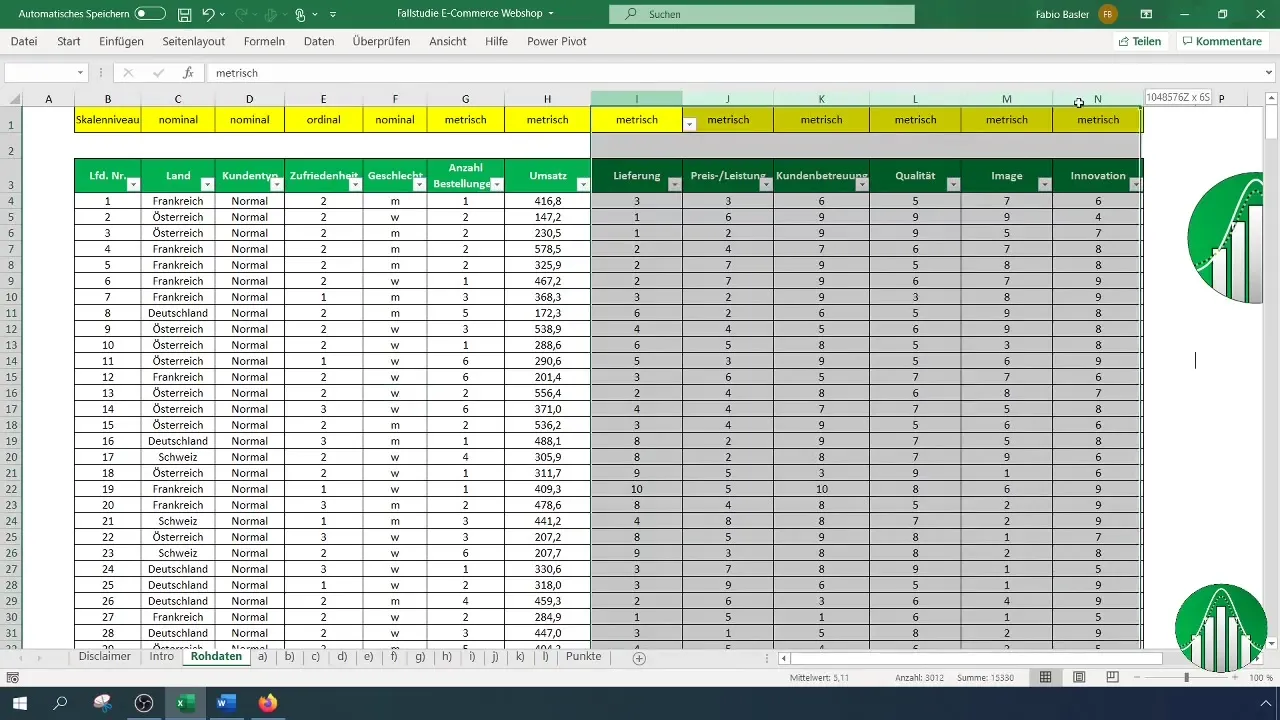
Перед проведением регрессионного анализа необходимо ввести все необходимые данные в Excel. Сюда входит список характеристик успеха (таких как доставка, соотношение цены и качества, обслуживание клиентов и т. д.) и оборот, который вы хотите проанализировать.

Шаг 2: Выберите независимые и зависимые переменные

Определите зависимую переменную - в данном случае оборот - и независимые переменные, которые вы хотите проанализировать. Отметьте данные для независимых переменных (X1 - X6) и зависимой переменной.

Шаг 3: Активируйте инструмент анализа данных

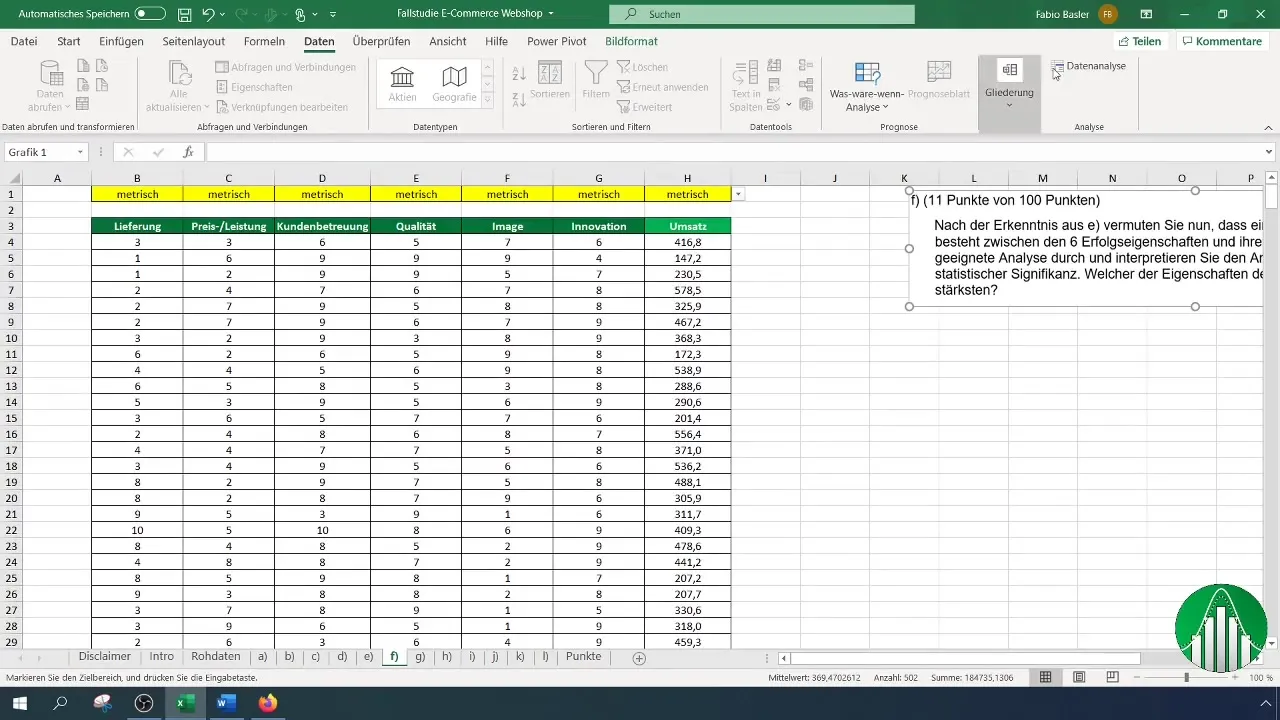
Активируйте инструмент анализа данных в Excel с помощью ленты. Перейдите в раздел "Данные" и найдите значок "Анализ данных", который предоставляет вам различные статистические функции.

Шаг 4: Выберите регрессию

Выберите опцию "Регрессия" из списка доступных инструментов анализа. Это позволит вам выполнить регрессионный анализ.

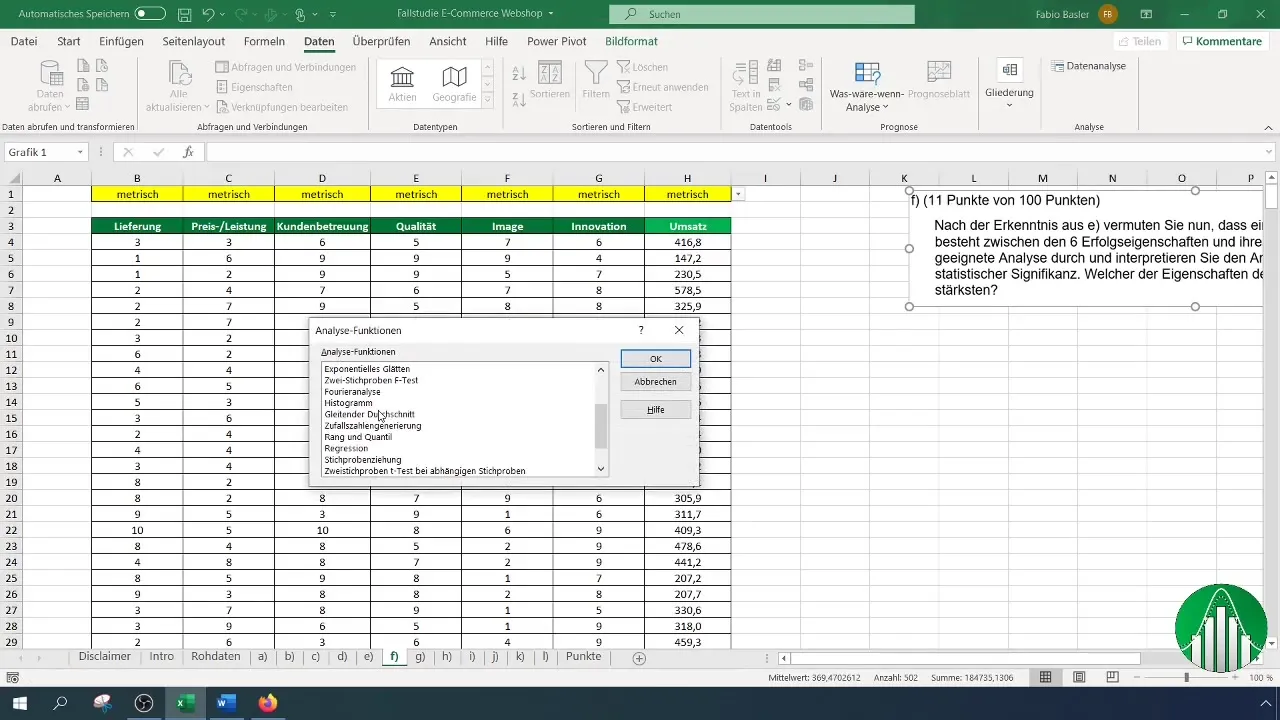
Шаг 5: Настройте поле ввода для регрессии

В поле ввода для регрессии выберите диапазон для зависимой переменной (продажи) и диапазон для независимых переменных (характеристики успеха). Не забудьте активировать метки, чтобы переменные были правильно идентифицированы.

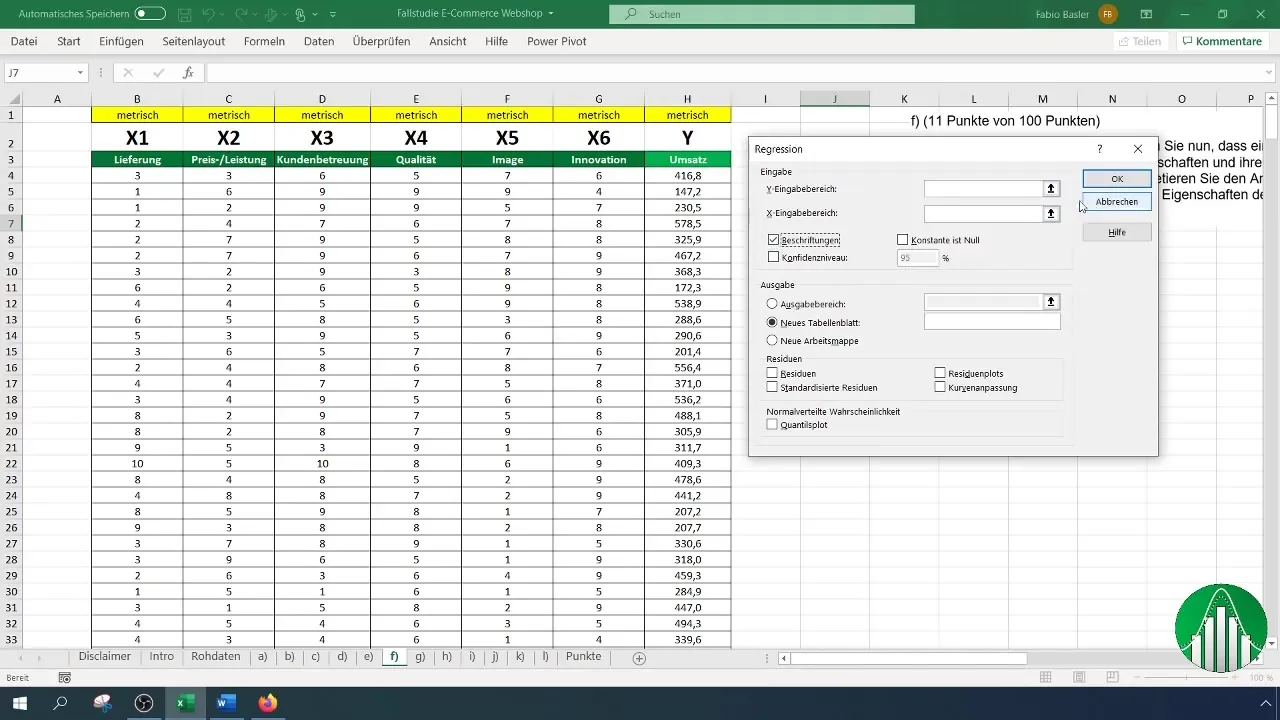
Шаг 6: Определите диапазон вывода

Определите область вывода, в которой вы хотите видеть результаты анализа. Вы можете расположить ее непосредственно справа от набора данных, чтобы данные оставались четкими.

Шаг 7: Проверьте уровень доверия

Убедитесь, что уровень доверия установлен на 95%, что является стандартным значением в большинстве статистических анализов. Это влияет на уверенность в результатах вашего анализа.

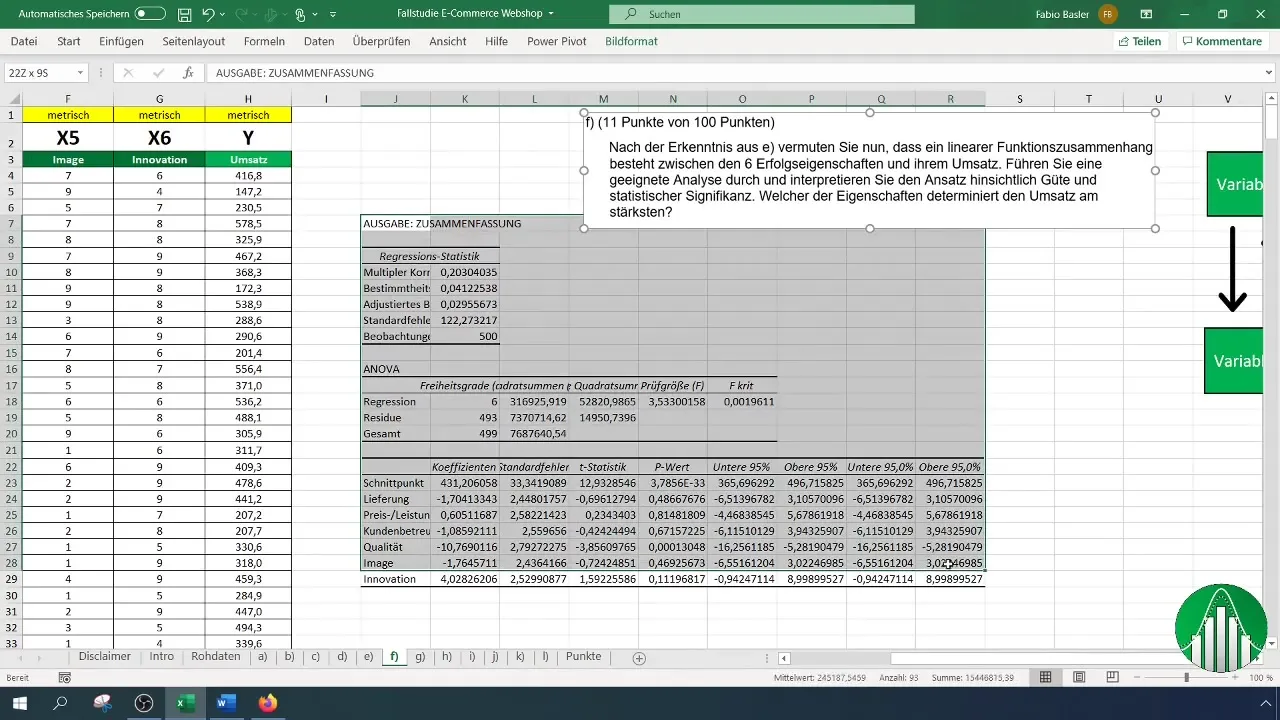
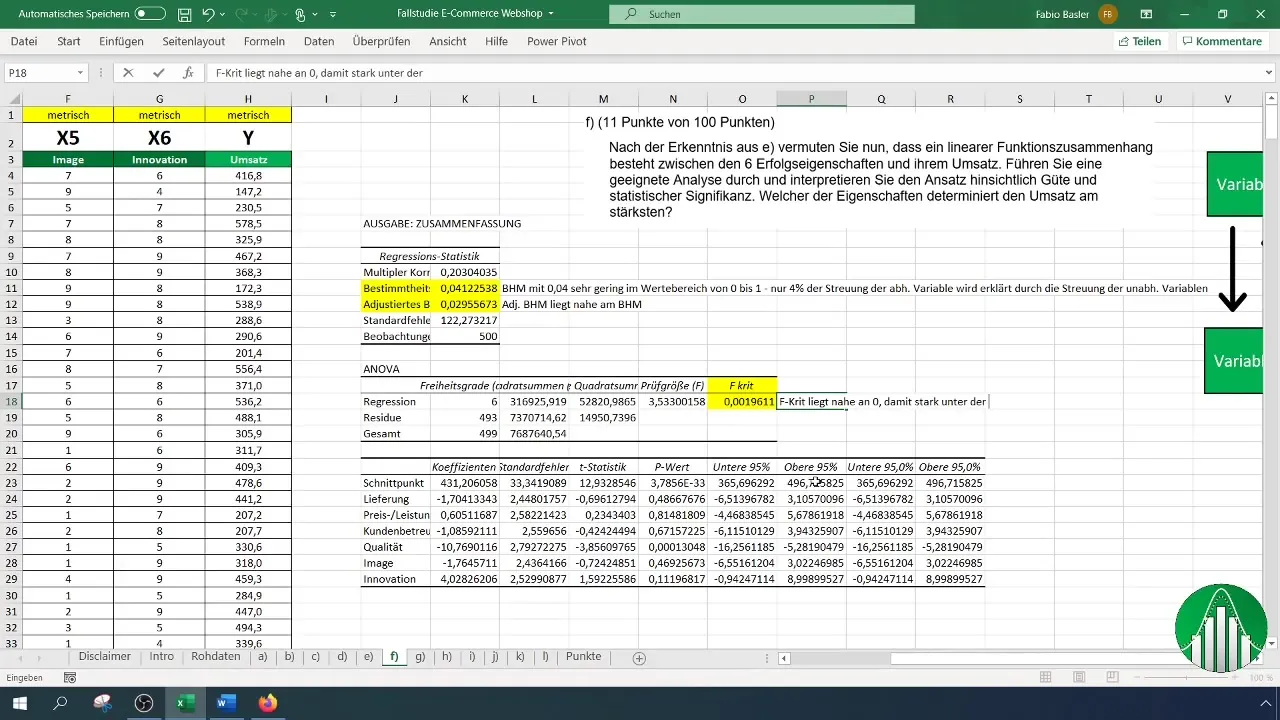
Шаг 8: Интерпретируйте результаты

После завершения анализа вы увидите результаты в Excel. Начните с интерпретации коэффициента детерминации (R²), который находится в диапазоне от 0 до 1. Значение 0,041 означает, что только 4 % дисперсии оборота объясняется независимыми переменными.

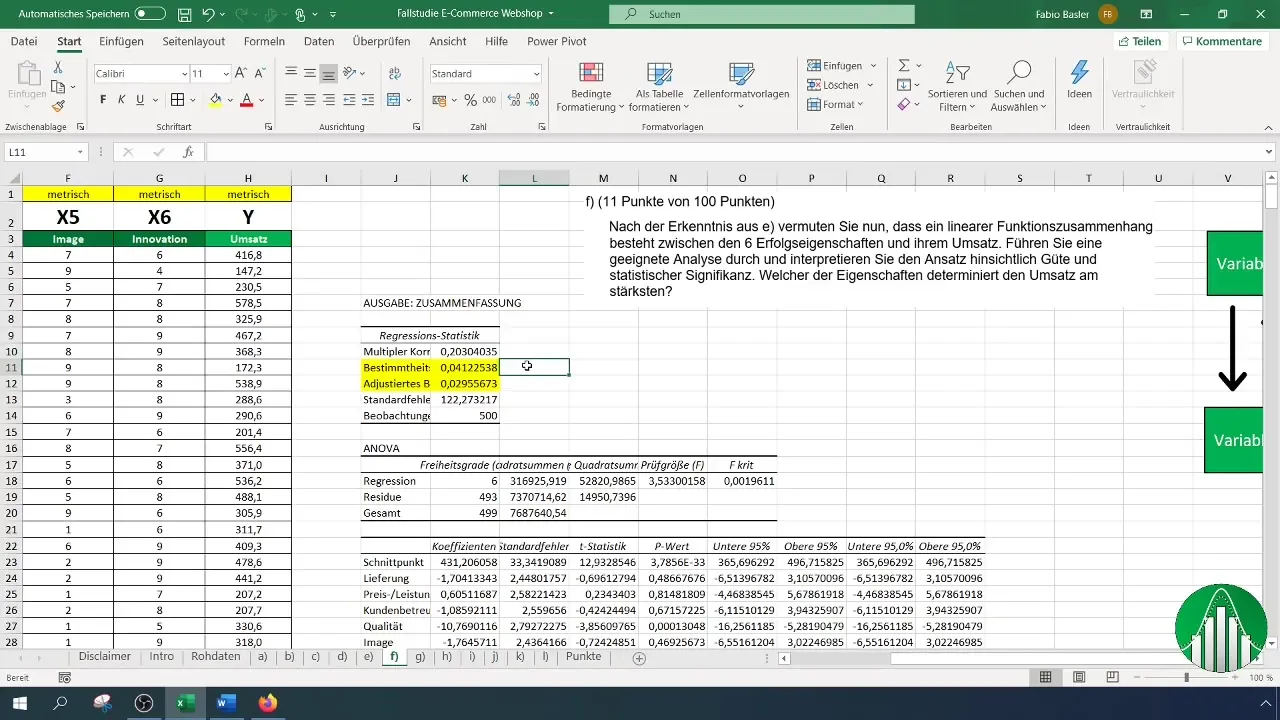
Шаг 9: Оценка статистической значимости

Проверьте p-значения и F-значение вашего анализа. Значение p-value, которое меньше 0,05, указывает на высокую статистическую значимость, что означает, что результаты ценны в контексте ваших гипотез.

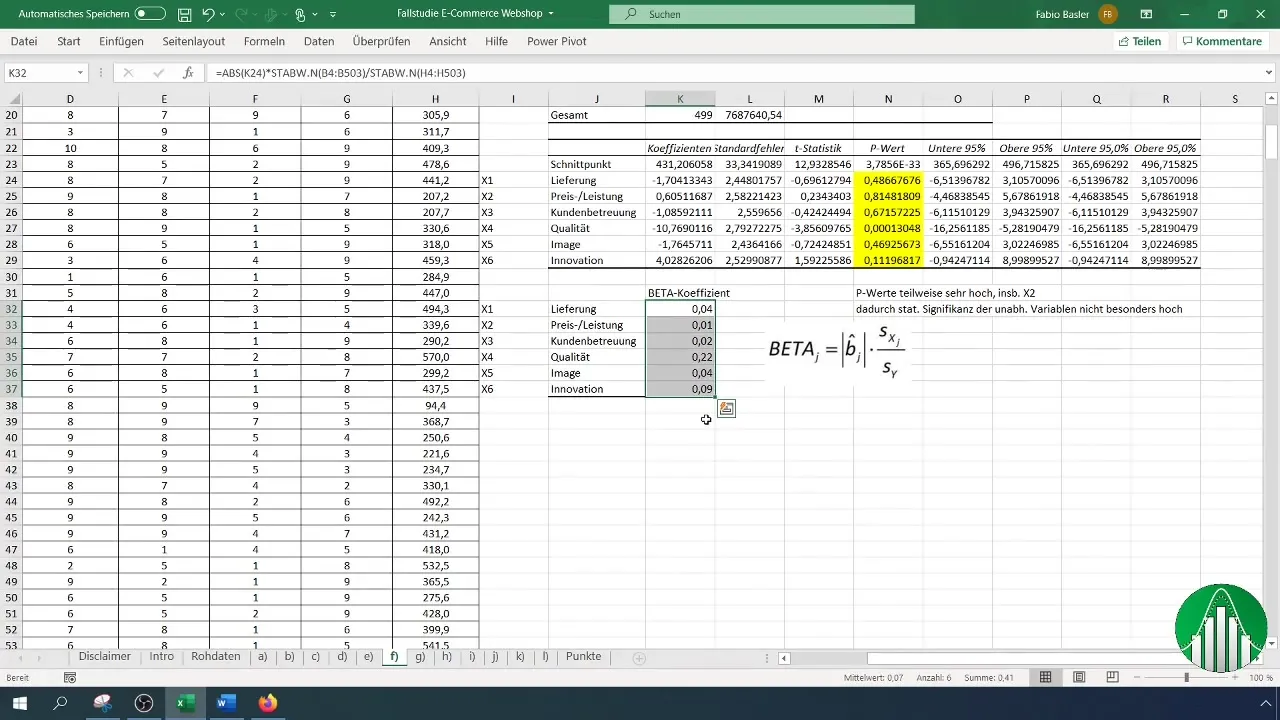
Шаг 10: Рассчитайте относительную важность переменных

Рассчитайте бета-коэффициент для каждой независимой переменной. Этот коэффициент показывает, насколько сильно независимая переменная влияет на зависимую переменную. Более высокие значения указывают на большую относительную важность.

Подведение итогов

В этом руководстве вы узнали, как выполнить регрессионный анализ в Excel. Вы узнали, как подготовить данные, провести анализ и интерпретировать результаты. Результаты этого метода очень важны для определения факторов, влияющих на продажи вашей компании.