Úspešný 1-SP test očakávanej hodnoty v Exceli

Štatistické testy sú kľúčovou súčasťou analyzovania údajov a rozhodovania. Zvlášť v oblasti biotechnológií môže byť rozhodujúce skúmať hypotézy o úspešnosti liečiv. V rámci tohto tutoriálu sa naučíš, ako efektívne vykonať Jednorozmerný test hypotéz (1-SP-Test) pre očakávanú hodnotu s poznatou varianciou v programe Excel .

Najdôležitejšie poznatky

Tento sprievodca ti poskytne:

• Teoretické základy 1-SP-Testu.
• Kroky pre vykonanie testu v programe Excel.
• Interpretáciu výsledkov.

Príprava údajov

Aby si mohol/-a vykonať 1-SP-Test v programe Excel, musíš mať najprv relevantné údaje. V našom príklade predpokladáme situáciu, keď analyzuješ úspešnosť liečiv. Je známe, že priemerná úspešnosť bola skôr 59 %, pri štandardnej odchýlke 19. Najskôr by si mal/-a vložiť svoje údaje do tabuľky v Exceli.

Uistite sa, že vaše údaje sú usporiadané do stĺpcov, aby ste na ne neskôr mohli ľahko pristupovať. Poznámkou je, že prehľadnosť vám pomôže ľahšie sledovať jednotlivé kroky.

Prehľad testu

1-SP-Test slúži na kontrolu, či sa priemerná hodnota úspechu signifikantne líši od predom definovanej hodnoty. V tomto prípade kontrolujeme, či sa úspešnosť 59 % v budúcnosti výrazne zvýši.

Formulovanie hypotéz

Hypotézy, ktoré stanovíš pre test, sú rozhodujúce:

• Nulová hypotéza (H0): Skutočná očakávaná hodnota je 59 (σ = 59 %).
• Alternatívna hypotéza (H1): Skutočná očakávaná hodnota je väčšia ako 59 %.

Pri formulovaní hypotéz by mal byť dôraz na to, čo presne musí byť testované, a ako sa to prejavuje v tvojom kontexte.

Je dôležité jasne rozlišovať medzi nulovou hypotézou a alternatívnou hypotézou, pretože tvoria základ pre nasledujúce výpočty.

Zber vzorky

Pre náš test vezmeme vzorku zo 500 liečiv. Je dôležité mať na pamäti, že výber vzorky by mal byť reprezentatívny a mala by byť garantovaná primeranosť pomocou príslušnej metódy, aby sa výsledky mohli realisticky preniesť na celkovú populáciu.

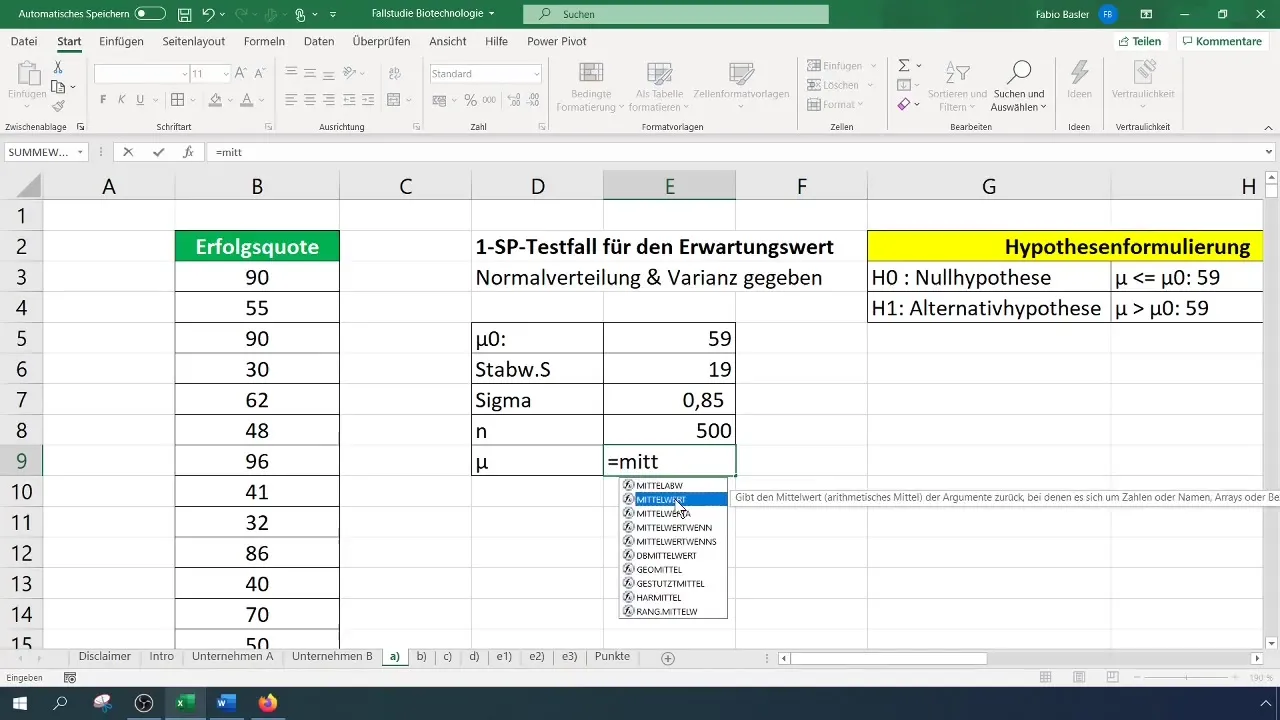
Pre test spočítaj najprv aritmetický priemer. To by sa malo ľahko dosiahnuť použitím príslušnej vzorca v Exceli.

Výpočet skúšobnej štatistiky

Skúšobnú štatistiku pre 1-SP-Test určíte pomocou nasledujúceho vzorca:

[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]

Tu (\bar{x}) predstavuje strednú hodnotu tvojej vzorky, (\mu_0) predstavuje predpokladanú strednú hodnotu (v tomto prípade 59), (\sigma) predstavuje štandardnú odchýlku (tu 19), a (n) označuje počet vzoriek (500).

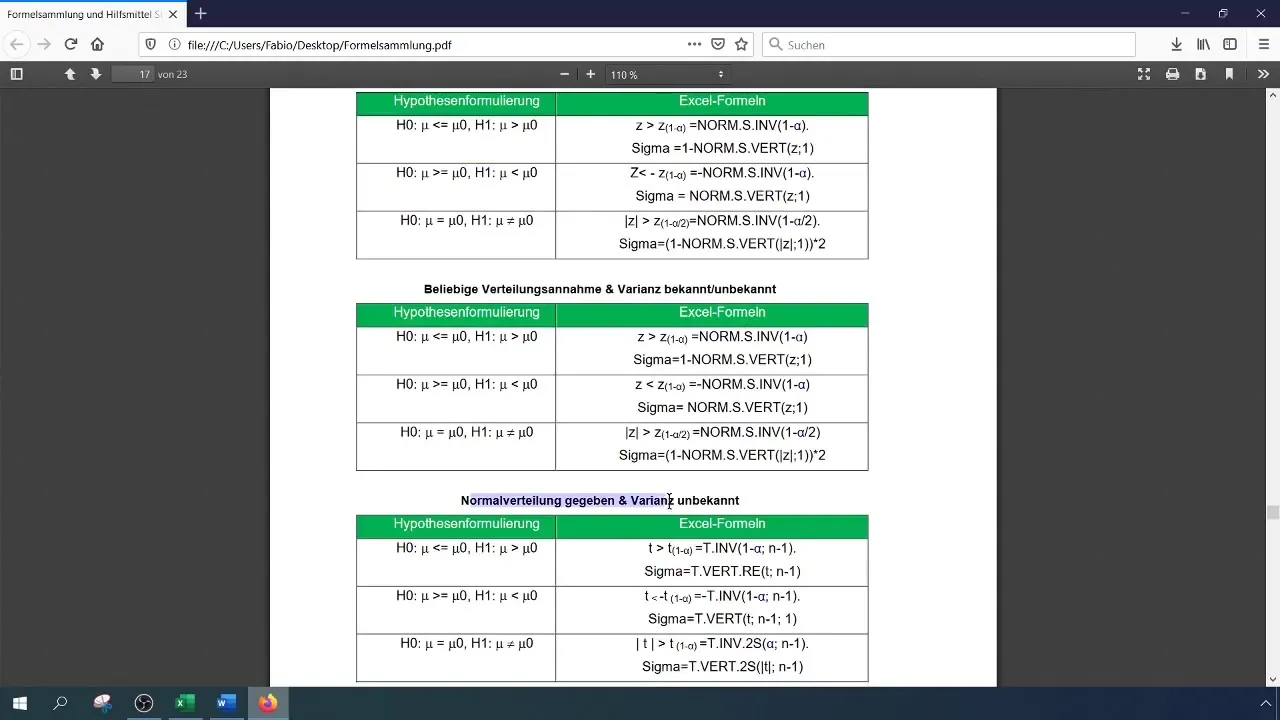
Po zapísaní hodnôt do vzorca spočítajte skúšobnú štatistiku a zistite, či je signifikantná alebo nie.

Stanovenie kritického hodnoty

Pre významovú hladinu 1 % (0,01) musíte prečítať alebo vypočítať kritickú hodnotu. V Exceli to môžete urobiť pomocou funkcie NORM.S.INV.

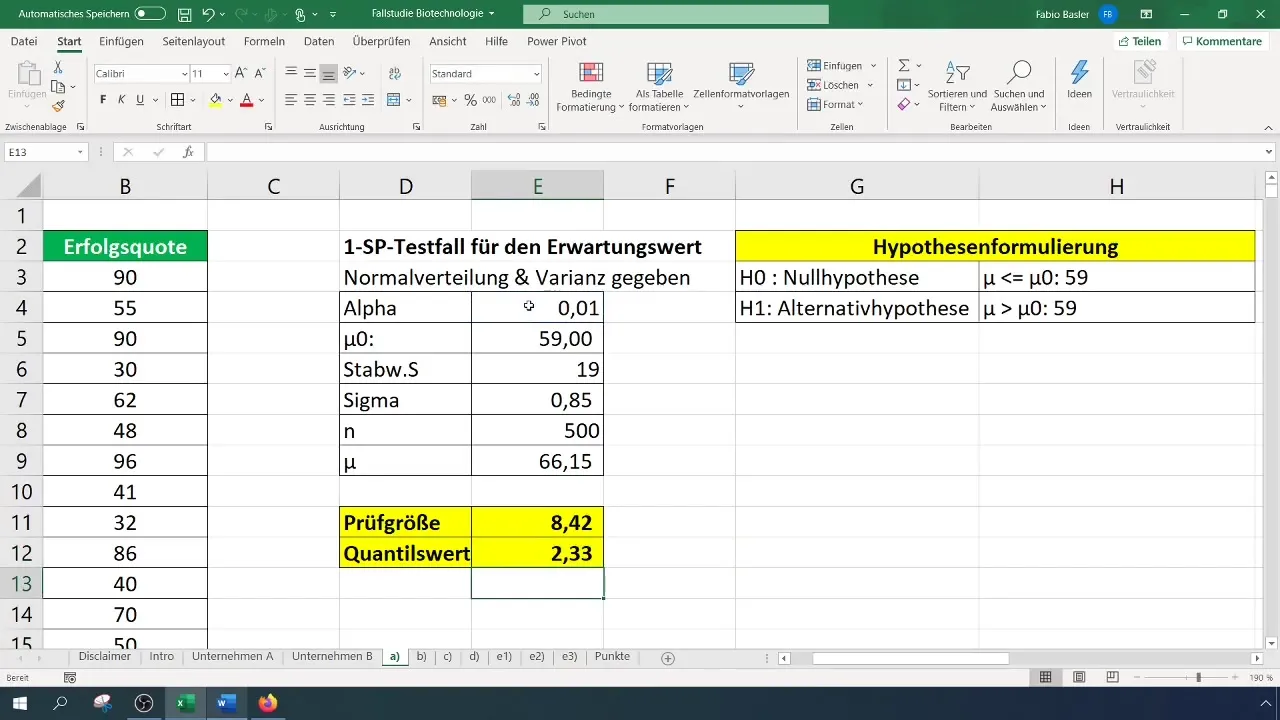
Vzorec znie:

[ \text{NORM.S.INV}(1 - \alpha) ]

Tu je (\alpha) hladina významnosti (0,01). Získaná hodnota bude slúžiť ako základ pre porovnanie so skúšobnou štatistikou.

Vykonanie testu

Po získaní skúšobnej štatistiky a kritického hodnoty porovnáte oboje:

• V prípade, že je skúšobná štatistika väčšia ako kritická hodnota, zamieta sa nulová hypotéza.
• Inak nie je možné zamietnuť nulovú hypotézu.

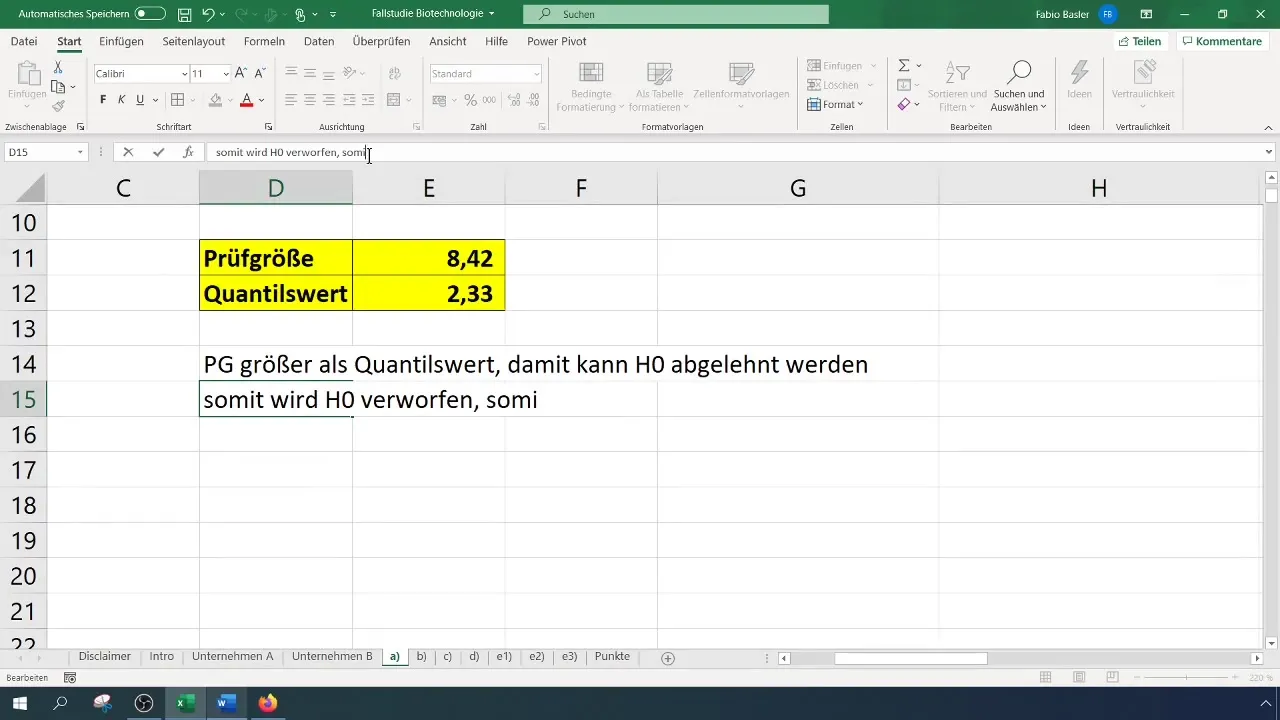
V našom prípade sme dostali testovaciu veličinu 8,4, ktorá prekračuje kritickú hodnotu 2,33. Preto môžeme zamietnuť nulovú hypotézu. To naznačuje, že úspešnosť bola signifikantne zlepšená.

Interpretácia výsledkov

Po vykonaní testu a získaní výsledkov by si ich mal interpretovať v jasný kontext. Zamietnutie nulovej hypotézy znamená, že testovaná nová hodnota sa významne líši od minulosti, v tomto prípade od 59%.

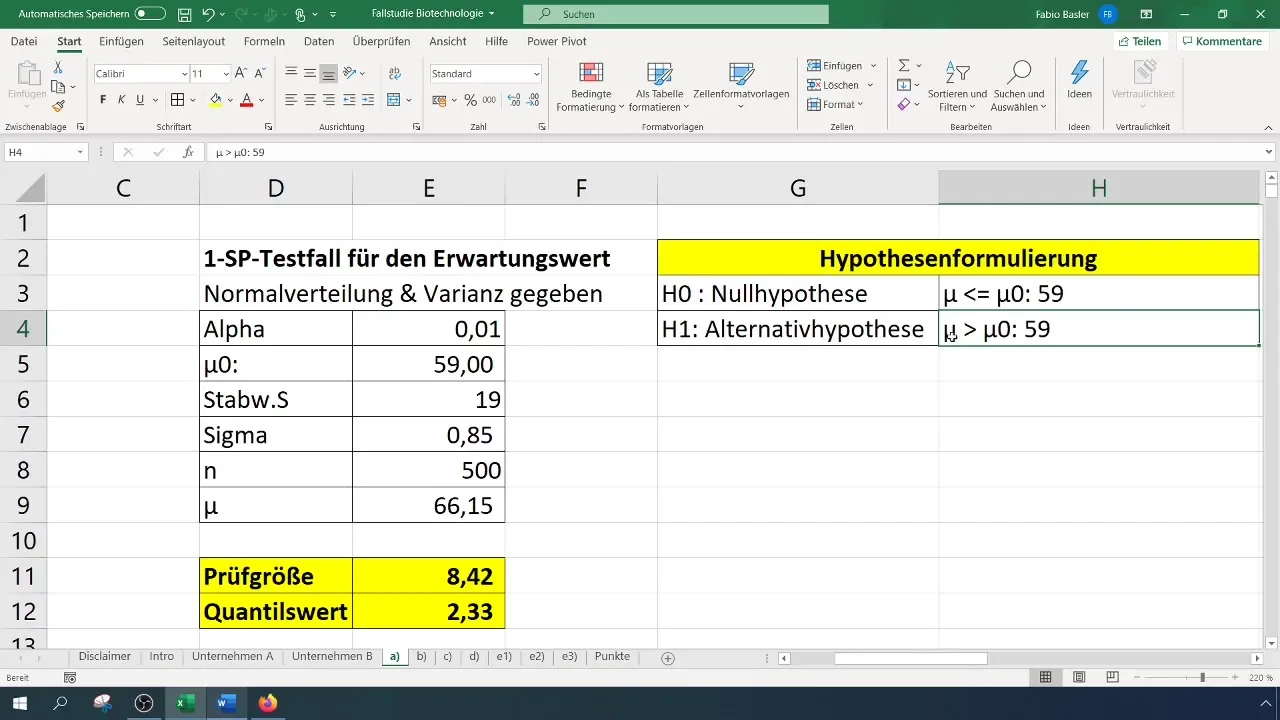
Tieto informácie sú pre stratégické rozhodovanie vo vašej spoločnosti veľmi dôležité. Potvrdzujú, že úsilie o zlepšenie úspešnosti bolo účinné.

Zhrnutie

V tomto tutoriáli ste sa naučili, ako vykonať test 1-SP pre očakávanú hodnotu v Exceli. S pomocou príkladu z prípadu ste mohli sledovať kroky od formulovania hypotéz cez výpočet údajov až po interpretáciu výsledkov. Tieto znalosti sú nielen užitočné pre vedecké vyhodnotenia, ale aj pre praktické aplikácie v podniku.