Dvojvýberový t-test je základný nástroj v štatistike, ak chcete skúmať rozdiel medzi dvomi priemermi. V tomto tutoriáli sa dozviete, ako jednoducho a efektívne vykonať tento test v Exceli. Na základe príkladu z biotechnológie sa naučíte porovnávať a štatisticky analyzovať úspešnosť dvoch súťažiacich spoločností.
Najdôležitejšie poznatky
- Použitie dvojvýberového t-testu na analýzu rozdielu medzi dvomi priemermi.
- Formulácia a overenie hypotéz.
- Použitie Excelu na výpočet a zobrazenie výsledkov.
Krok za krokom sprievodca
Najprv začneme vytvorením potrebných údajov a vykonaním testu v Exceli.
Krok 1: Príprava údajov
Začnite zbieraním hrubých údajov o úspešnosti oboch spoločností. Predpokladajme, že máte k dispozícii údaje o spoločnostiach A a B s jednou vzorkou obsahujúcou 100 záznamov pre každú spoločnosť.

Krok 2: Vypočet počtu vzoriek a priemerov
Vytvorte v Exceli tabuľku na porovnanie vzoriek a ich priemerov. Najskôr vypočítajte počet vzoriek (N) pre obe spoločnosti a ich priemer (X).

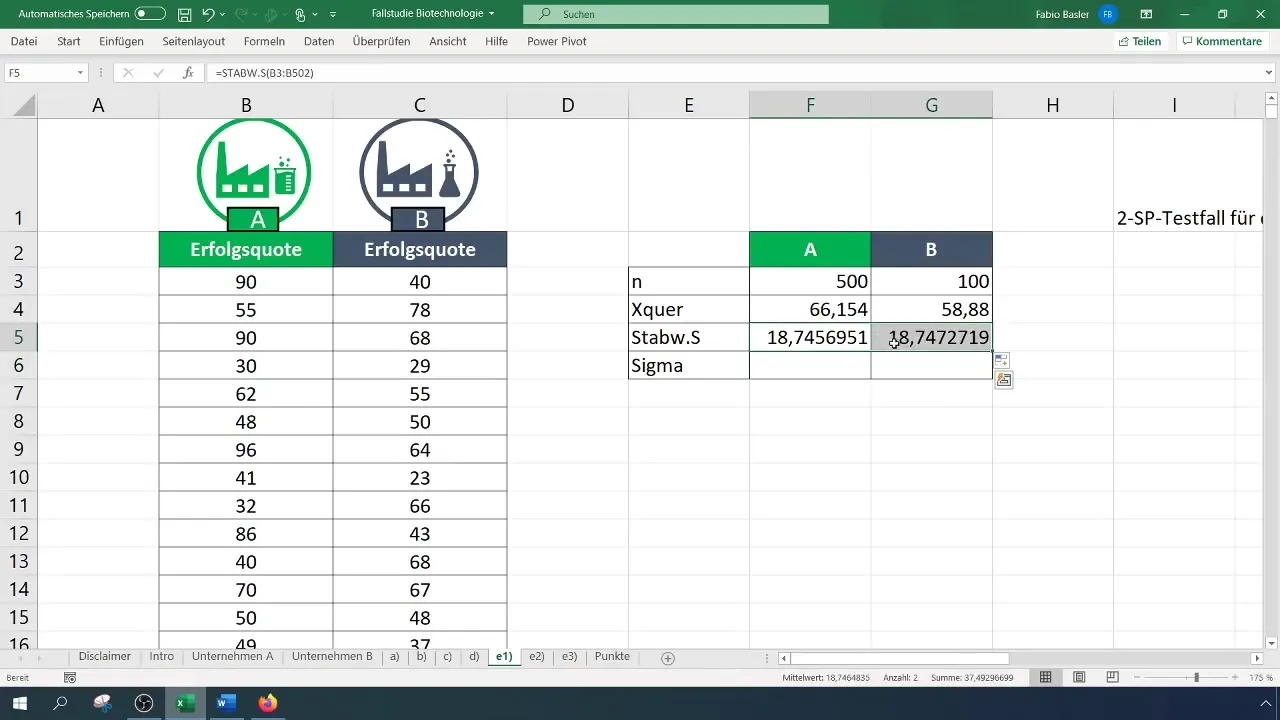
Krok 3: Určenie smerodajných odchýlok
Vypočítajte smerodajné odchýlky pre obidve spoločnosti. Tieto hodnoty sú dôležité pre výpočet rozptylu a nasledujúcich výpočtov.
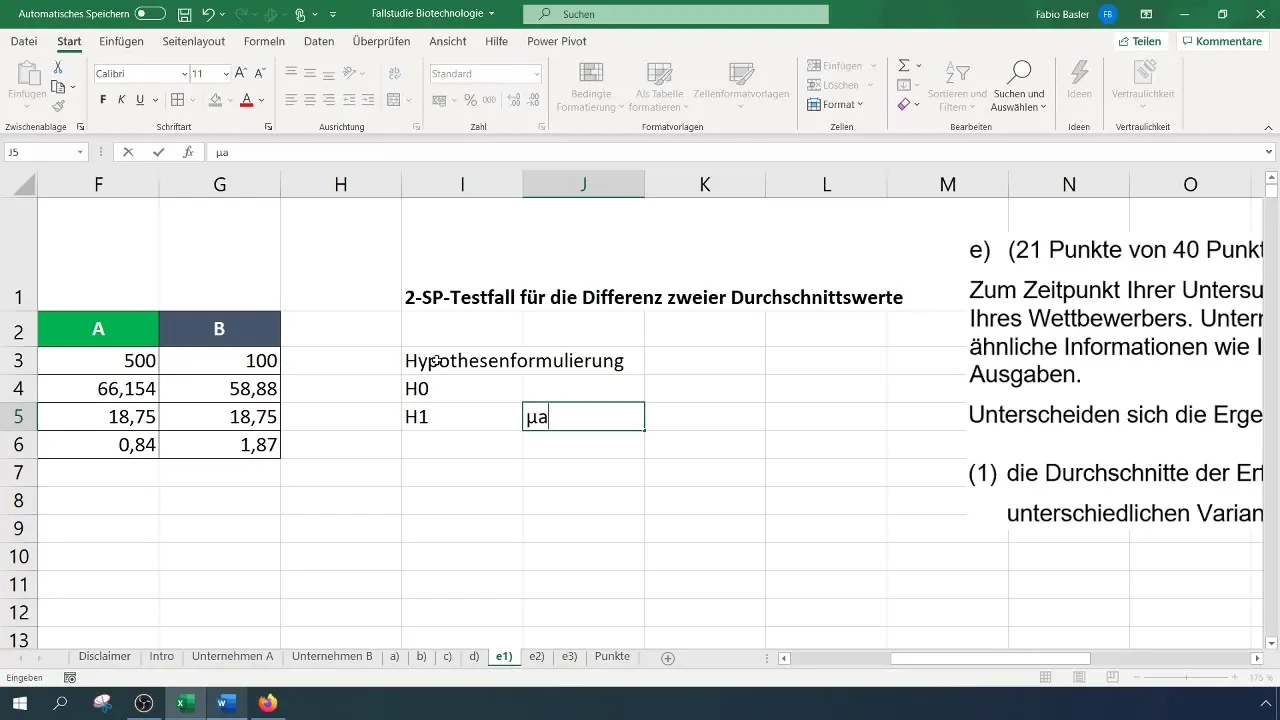
Krok 4: Formulácia hypotéz
Formulujte nulovú hypotézu (H_0): Priemery úspešností spoločností A a B sú rovnaké. Alternatívna hypotéza (H_1): Priemery úspešností sú rôzne.
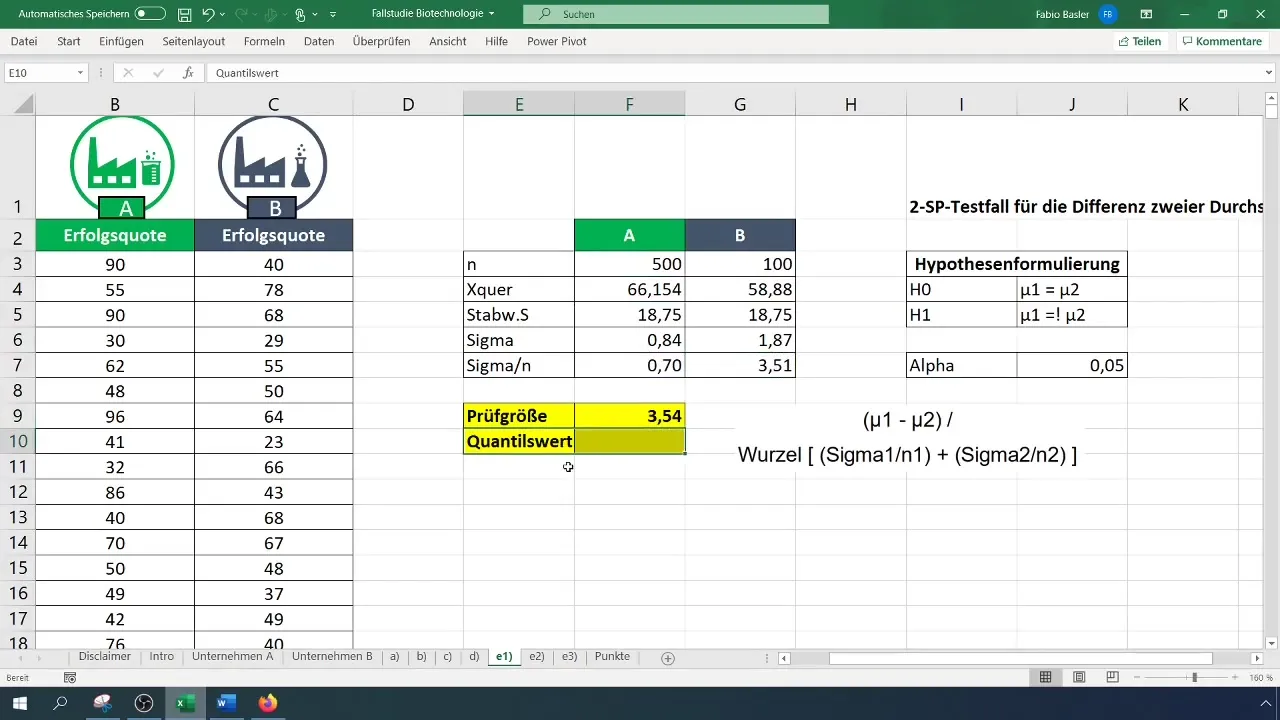
Krok 5: Výpočet testovej štatistiky
Na výpočet testovej štatistiky použite vzorec pre t-test. Vypočítajte rozdiel v priemeroch a vydeľte ho odmocninou súčtu rozptylov pre každú vzorku.
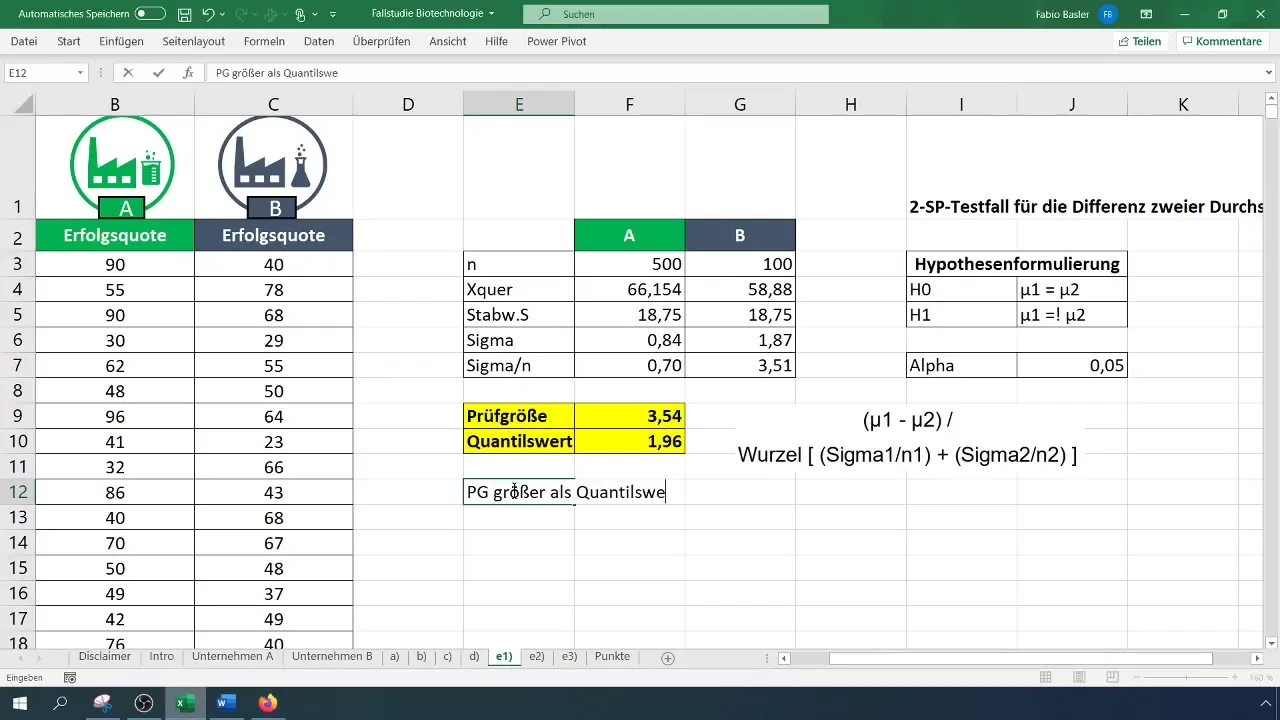
Krok 6: Určenie kritického hodnoty
Použite oboustranné t-rozdelenie na nájdenie kritického hodnoty. Nastavte hladinu alfa na 0,05. Skontrolujte tabuľku t-rozdelenia alebo vypočítajte faktor priamo v Excele.
Krok 7: Rozhodnutie o hypotéze
Porovnajte vypočítanú testovú štatistiku s kritickým hodnotou. Ak je testová štatistika väčšia ako kritická hodnota, zamietnite nulovú hypotézu (H_0) a tým potvrďte alternatívnu hypotézu (H_1).
Krok 8: Interpretácia výsledkov
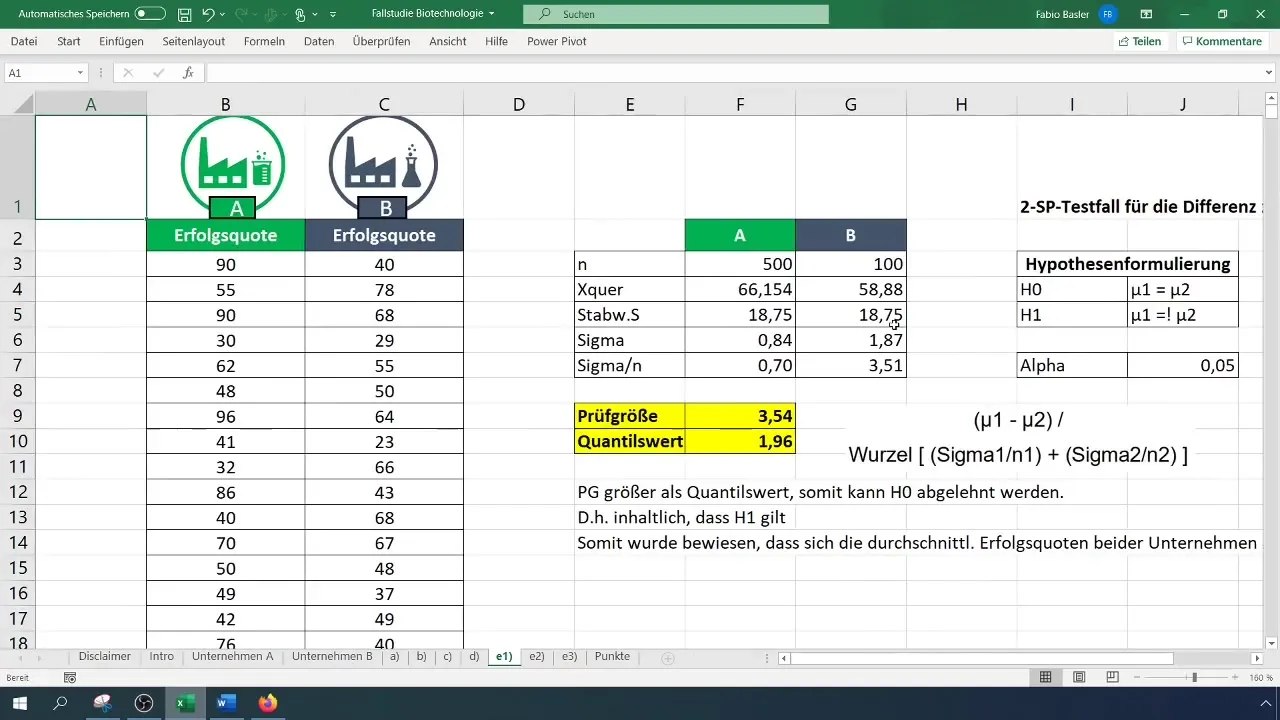
Nakoniec interpretujte výsledok. V tomto príklade boli zisté signifikantné rozdiely v priemerných úspešnostiach oboch spoločností.
Zhrnutie
Naučili ste sa, ako vykonávať dvojvýberový t-test v Exceli na skúmanie rozdielov v priemeroch dvoch skupín. Kľúčové kroky od prípravy údajov cez formuláciu hypotéz až po interpretáciu výsledkov sú rozhodujúce pre urobenie platných a informovaných rozhodnutí.
Často kladené otázky
Čo je dvojvýberový t-test?Dvojvýberový t-test porovnáva priemery dvoch skupín, aby určil, či sú signifikantne odlišné.
Ako formulujem hypotézy?Nulová hypotéza (H_0) tvrdí, že priemery sú rovnaké, zatiaľ čo alternatívna hypotéza (H_1) hovorí, že sú odlišné.
Ako vypočítam testovú štatistiku?Testová štatistika sa vypočíta ako podiel rozdielu priemerov a odmocniny súčtu rozptylov.
Čo robiť po výpočte?Porovnajte testovú štatistiku s kritickou hodnotou, aby ste sa rozhodli, či môžete zamietnuť nulovú hypotézu.
Prečo je dôležitá smerodajná odchýlka?Smerodajná odchýlka pomáha pochopiť variabilitu údajov, ktorá je kľúčová pre výpočet testovej štatistiky.


