Chi-štvorec na prispôsobenie test predstavuje jednoduchú metódu na overenie hypotézy, či daná rad dát nasleduje normálne rozdelenie. V tejto príručke sa naučíte, ako vykonať test chi-štvorca v Excele na zistenie, či obraty smartfónov nasledujú normálne rozdelenie. Postupne prejdeme cez proces od vytvorenia frekvenčnej tabuľky po vypočítanie testovej hodnoty a porovnanie s kritickou hodnotou chi-štvorca.
Najdôležitejšie poznatky
- Test prispôsobenia chi-štvorca pomáha pri overovaní normálnych rozdelení.
- Je dôležité vytvoriť frekvenčnú tabuľku.
- Testovacia hodnota sa porovnáva s kritickou hodnotou, aby sa hypotéza buď zamietla alebo prijala.
Postup krok za krokom
Krok 1: Príprava dát
Na vykonanie testu chi-štvorca musíte mať najskôr dáta. Skopírujte obraty smartfónov do listu Excelu. Uistite sa, že vaše dáta sú usporiadané v jednom stĺpci.

Krok 2: Vytvorenie histogramu
Pre získanie prvých vizuálnych náznakov o rozdelení vytvorte histogram vašich dát. Prejdite na „Vložiť“ a vyberte „Grafy“. Pridajte histogram tým, že zvolíte rozsah dát.
Krok 3: Vytvorenie frekvenčnej tabuľky
Na test chi-štvorca potrebujete frekvenčnú tabuľku. Najskôr určte počet tried pre vašu tabuľku - v tomto prípade používame šesť tried. Vypočítajte šírku intervalov a vytvorte tabuľku podľa toho.
Krok 4: Vypočítanie frekvencií
Teraz musíte vypočítať pozorované frekvencie pre každú triedu. Prejdite na „Dáta“ a vyberte „Analýza dát“. Zvoľte vstupný rozsah pre vaše dáta a krajné hodnoty tried. Určite výstupný rozsah pre frekvenčnú tabuľku.
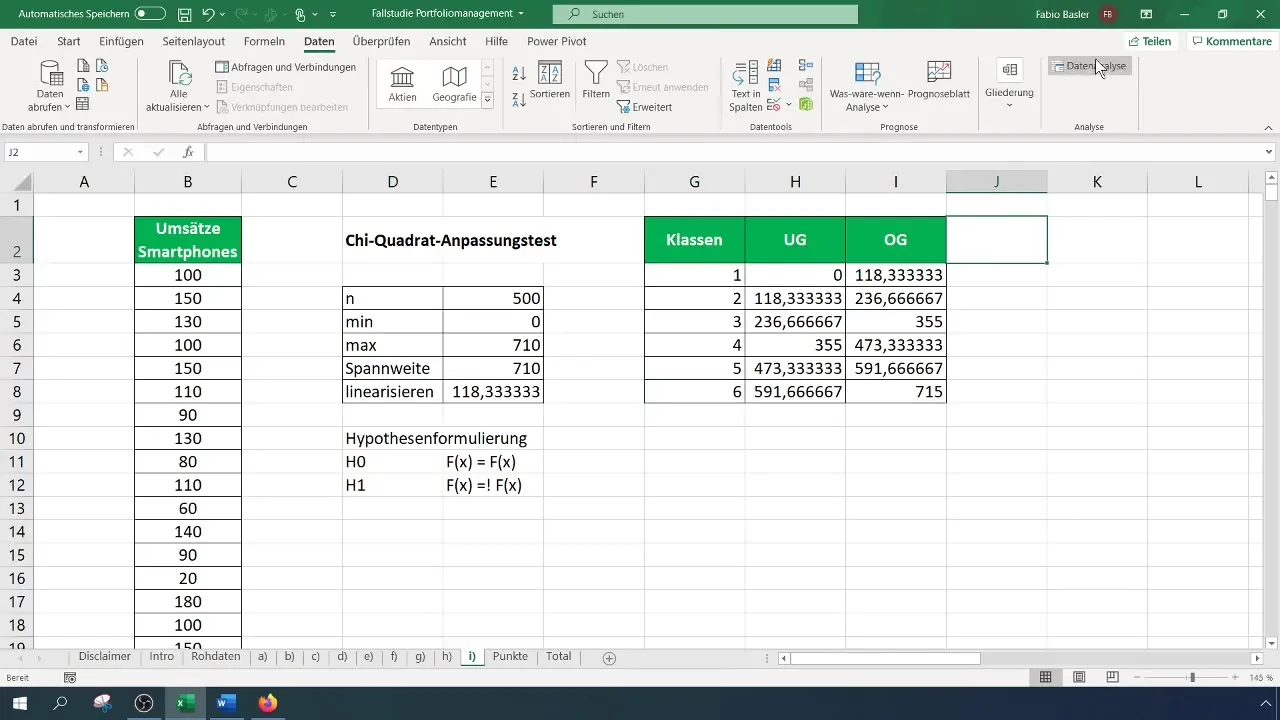
Krok 5: Vypočítanie očakávaných frekvencií
Pre výpočet očakávaných frekvencií určite pravdepodobnosti pre každú triedu na základe predpokladaného normálneho rozdelenia. Potrebujete priemer a štandardnú odchýlku vašich dát.
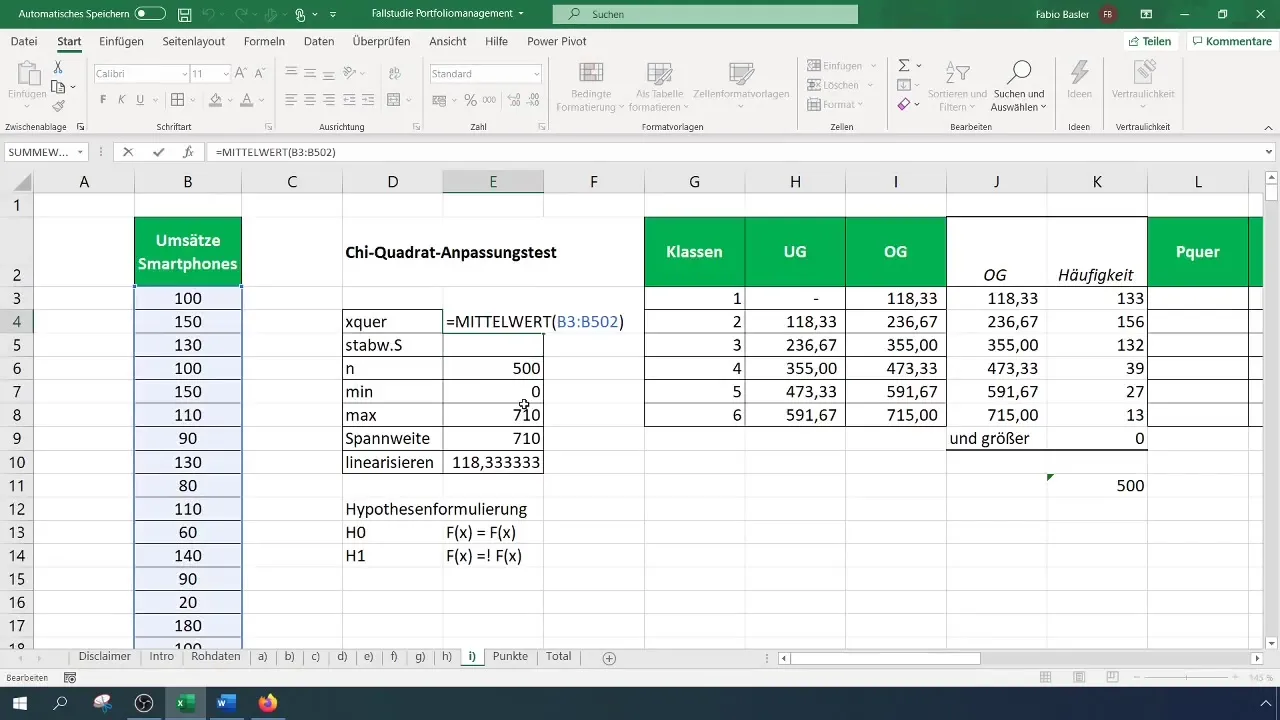
Krok 6: Výpočet testovej hodnoty
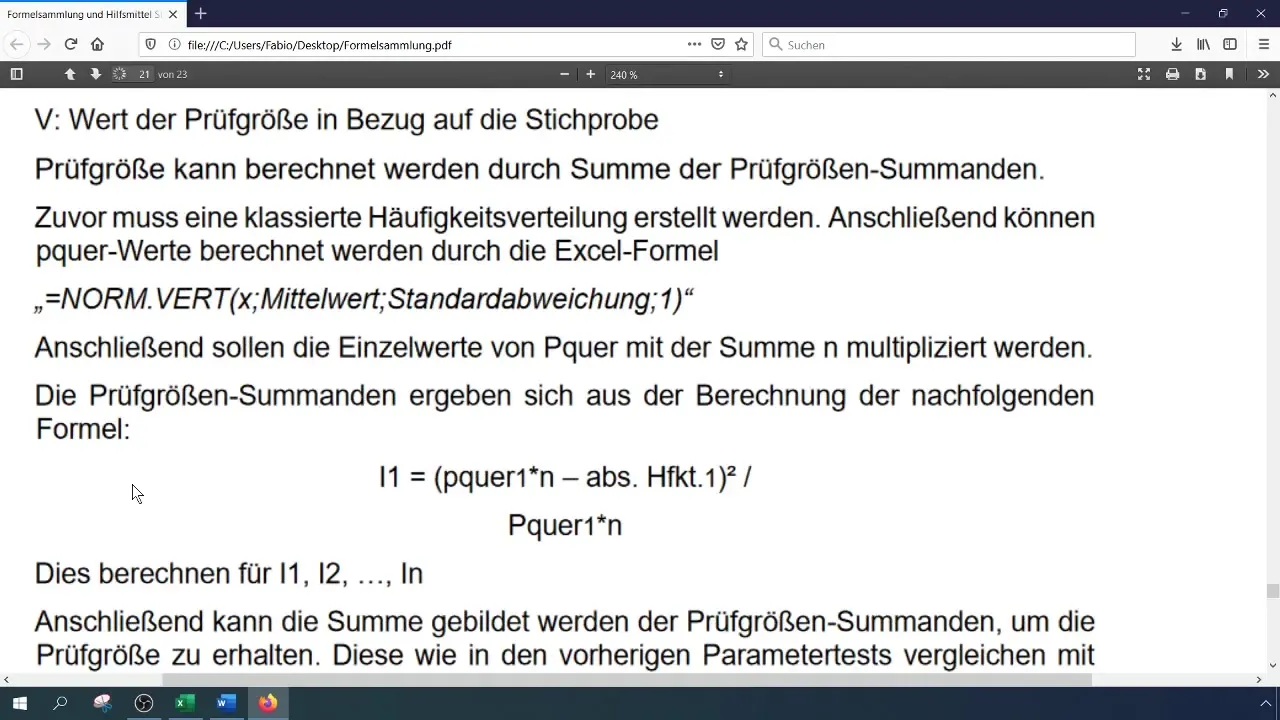
Vypočítajte testovú hodnotu (chi-štvorec) podľa vzorca:
[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]
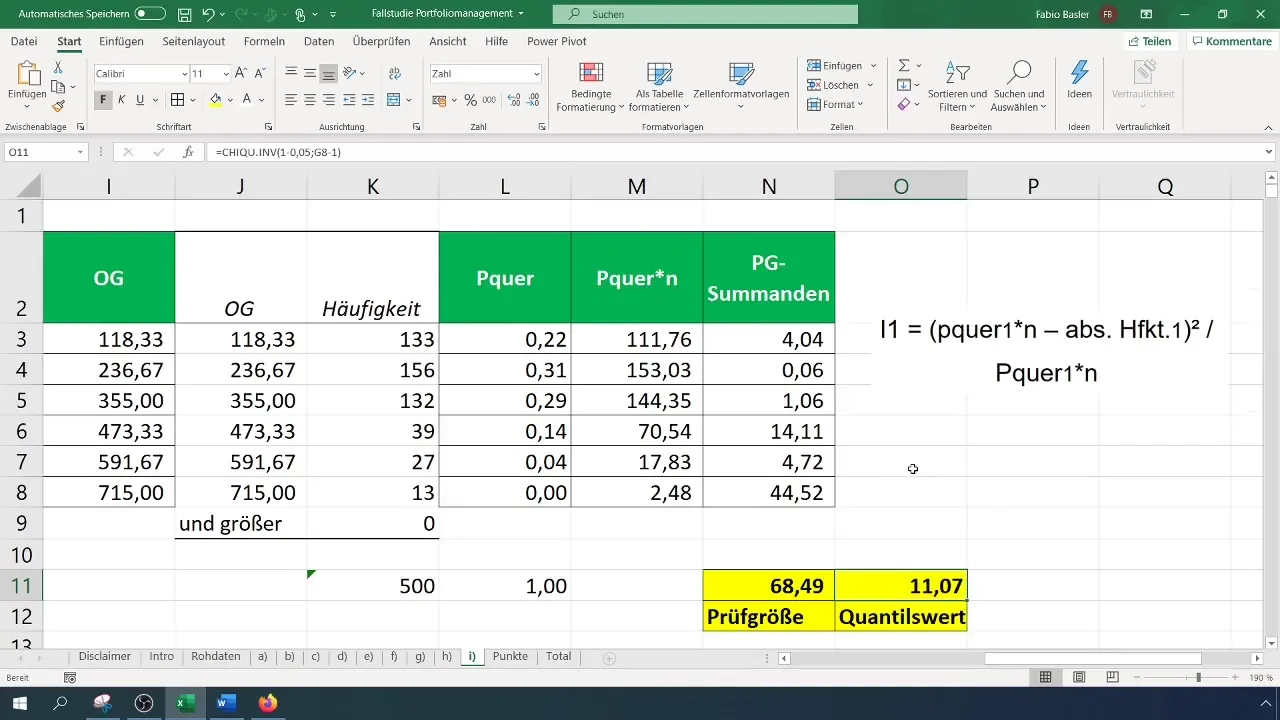
kde (O_i) sú pozorované hodnoty a (E_i) sú očakávané frekvencie. Túto výpočet môžete vykonať v Exceli ukladaním jednotlivých komponentov do samostatných buniek.
Krok 7: Výpočet kritického hodnoty
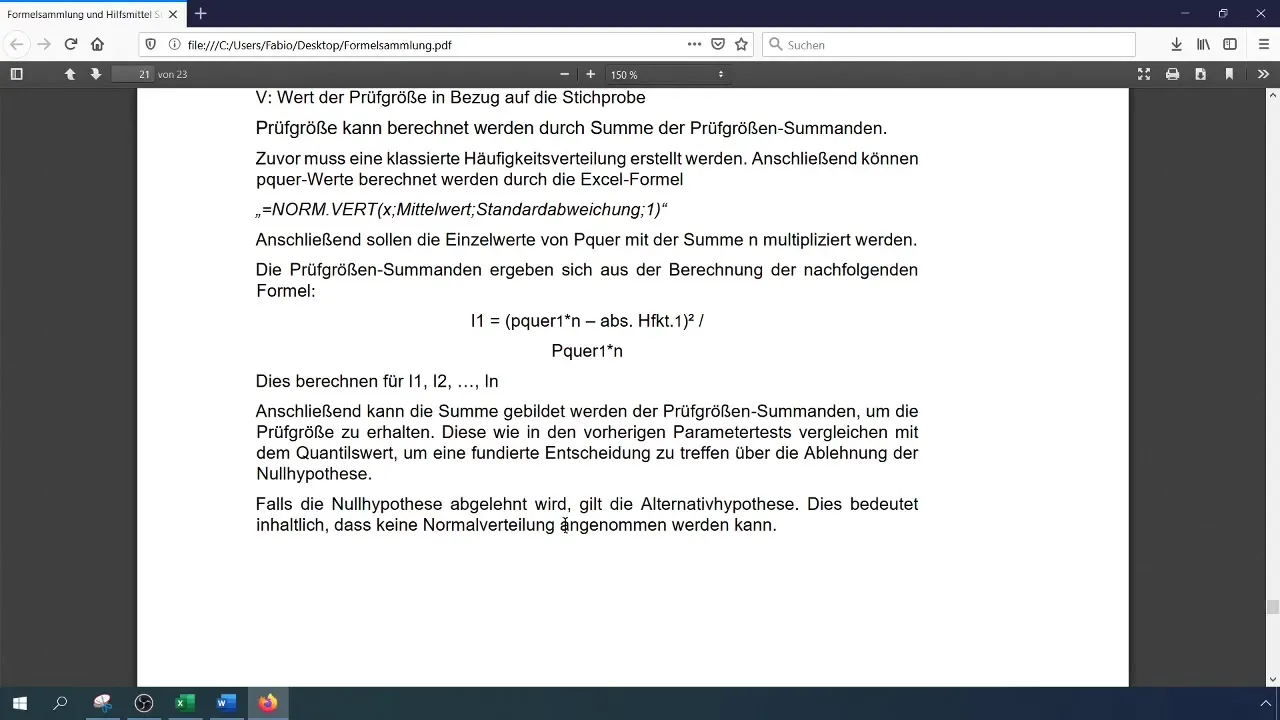
Pre vyhodnotenie testovej hodnoty musíte vypočítať kritickú hodnotu ( \chi^2 ) pre vašu úroveň istoty a počet stupňov voľnosti. Počet stupňov voľnosti pre test chi-štvorca je (k - 1), pričom (k) je počet tried.
Krok 8: Overenie hypotéz
Porovnajte vašu vypočítanú testovú hodnotu s kritickou hodnotou. Ak je testová hodnota väčšia ako kritická hodnota, zamietnite nulovú hypotézu, čo znamená, že dáta nie sú normálne rozdelené. V opačnom prípade prijmite nulovú hypotézu.
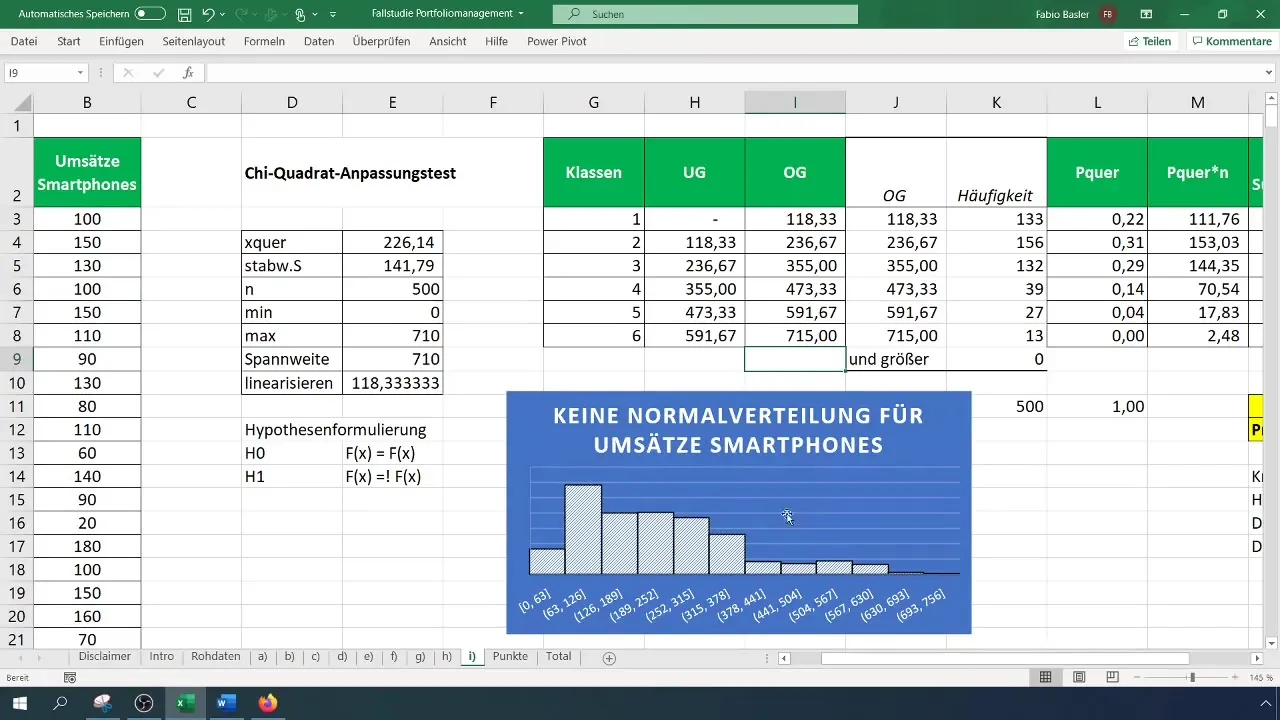
Krok 9: Zhrnutie výsledkov
Zachovajte svoje výsledky a rozšírte ich o grafické údaje a hypotézy. Nezabudnite skontrolovať svoj histogram, aby ste vizuálne potvrdili, že rozdelenie nie je normálne.
Zhrnutie
Počas tohto návodu si osvojíte, ako v systéme Excel vykonať test prispôsobenia chi-kvadrát pre analýzu normálneho rozdelenia tržieb z smartfónov. Postup zahŕňa vytvorenie zaraďovacej frekvencie, výpočet očakávaných frekvencií, testovaciu štatistiku a nakoniec porovnanie s kritickou hodnotou.
Často kladené otázky
Čo je Chi-kvadrátový test prispôsobenia?Test prispôsobenia chi-kvadrátom testuje, či pozorované frekvenčné rozdelenie zodpovedá normálnemu rozdeleniu.
Koľko tried potrebujem pre frekvenčnú tabuľku?V zásade je rozumné mať minimálne 5 až 10 tried na výstižnú analýzu dát.
Čo robiť, ak je nulová hypotéza odmietnutá?Ak odmietnete nulovú hypotézu, znamená to, že údaje nie sú normálne distribuované.
Ako vypočítať kritickú hodnotu chi-kvadrátu?Kritická hodnota sa číta z tabuľky distribúcie chi-kvadrátu na základe stupňov voľnosti a požadovaného významového úrovne.


