Výpočet dôveryhdodstopove intervalov je podstatnou súčasťou štatistickej analýzy, najmä ak ide o odvodenie záverov o základnej populácii zo vzorky. V tomto návode vám ukážem, ako v Excel vypočítať dvostranný dôveryhodnostný interval pre priemerný obrat v prieskume. Dozviete sa, aké rôzne kroky sú potrebné na prechod od hrubých údajov k finálnemu dôveryhodnostnému intervalu a ako túto metodiku realizovať v Exceli.
Najdôležitejšie poznatky
- Dvojstranný dôveryhodnostný interval udáva, v ktorých medziach môže byť skutočný priemer obratu s určitou pravdepodobnosťou dôveryhodnosti.
- Na výpočet potrebujete priemer, štandardnú odchýlku, veľkosť vzorky a príslušný t-kvantil.
- V Exceli máte k dispozícii potrebné funkcie na výpočet týchto hodnôt a vizuálne zobrazenie dôveryhodnostného intervalu.
Krok za krokom sprievodca
Krok 1: Príprava údajov
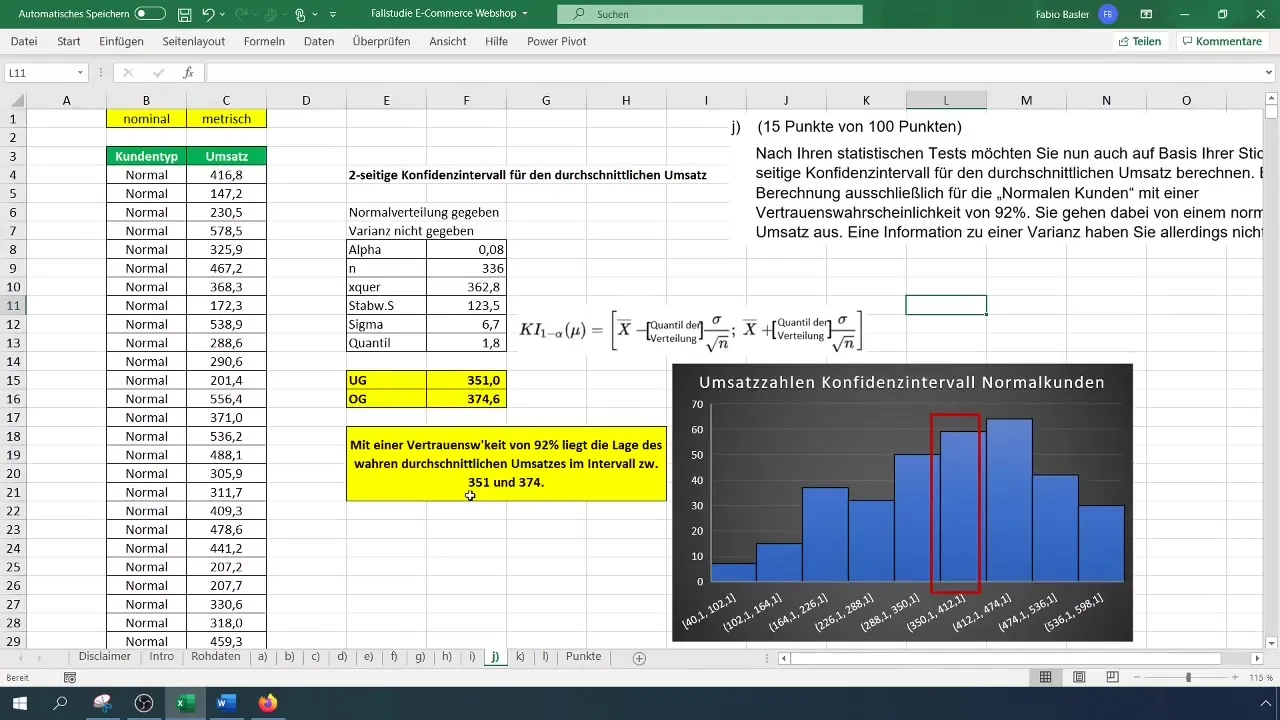
Najprv si pripravte relevantné údaje v Exceli. V tomto príklade budeme zvažovať iba bežných zákazníkov, pretože priemer obratu sa má vypočítať len pre túto skupinu.

Môžete označiť a skopírovať údaje zo svojho pracovného hárka a vložiť ich do nového rozsahu. Tým sa filtrované údaje pre príslušné skupiny zákazníkov.
Krok 2: Zozbieranie základných informácií
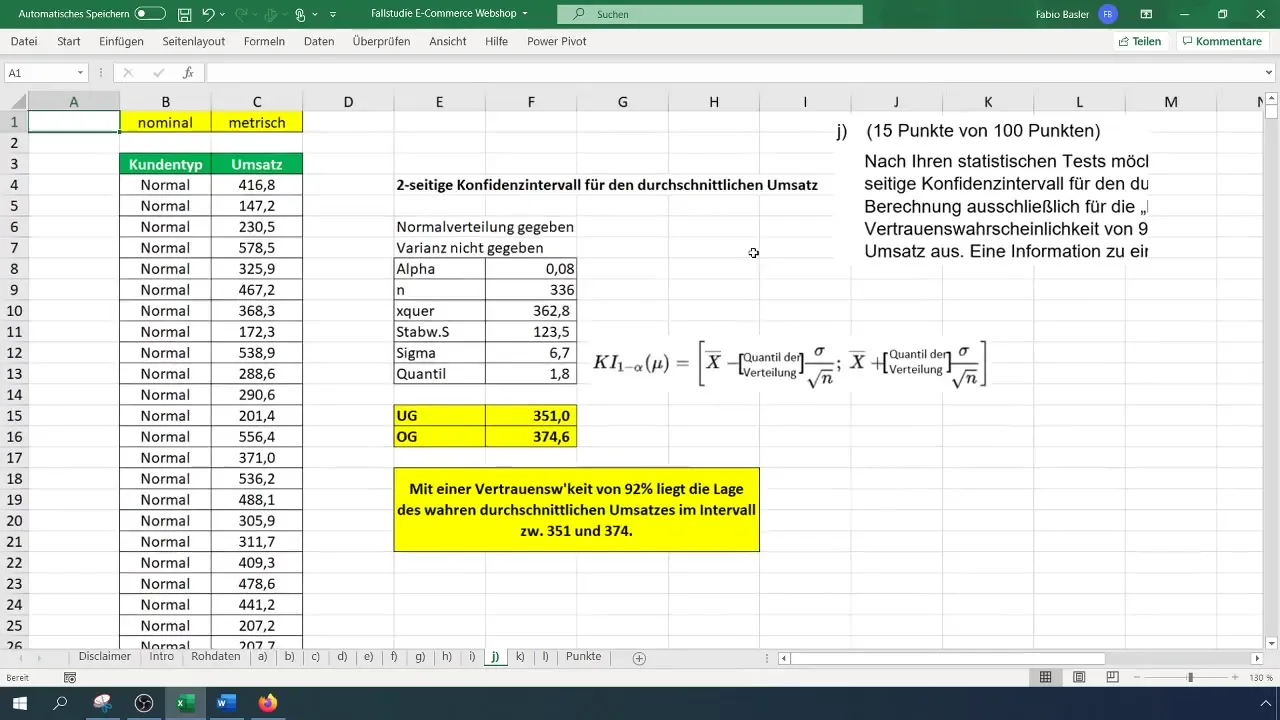
Vytvorte jednoduchú tabuľku v Exceli, v ktorej uvediete všetky dôležité parametre. Ide o veľkosť vzorky (n), priemer (x̄), štandardnú odchýlku (σ) a príslušný kvantil t. Už vieme, že predpokladáme normálne rozdelenie a nemáme k dispozícii varianciu.

Krok 3: Výpočet veľkosti vzorky (n)
Na zistenie počtu pozorovaní pre bežných zákazníkov musíte vyrezať príslušné údaje a použiť FORMULU =POČET() na zistenie počtu. V tomto prípade by ste mali z filtrovaných údajov získať 336 pozorovaní.
Krok 4: Výpočet priemeru (x̄)
Vypočítajte priemer obratov použitím vzorca =PRIEMER(). Tým získate priemerný obrat pre bežných zákazníkov, ktorý v našom príklade predstavuje 362,80 eur.
Krok 5: Stanovenie štandardnej odchýlky (σ)
Na výpočet štandardnej odchýlky použite vzorec =ODCHYLKA.STANDARDNÍ(). Táto hodnota je potrebná pre induktívnu štatistiku, preto používame štandardnú odchýlku pre vzorku. Vypočítaná hodnota je 123 eur.
Krok 6: Sigma (σ / √n) vypočítať
Teraz vypočítate štandardnú odchýlku pre priemer vydelením štandardnej odchýlky štvorcovou odmocninou vzorkovej veľkosti. Použite vzorec: =Štandardná odchýlka/ODMOCNINA(VelkostVzorky).
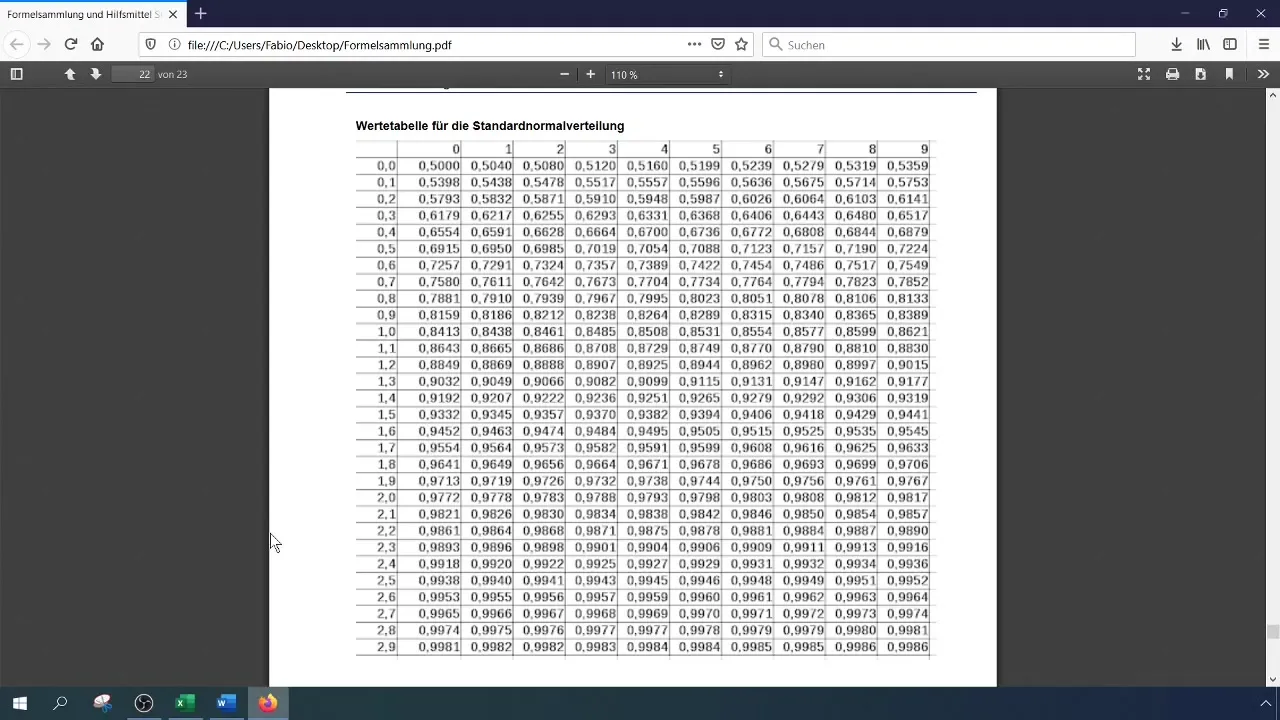
Krok 7: Nájsť t-kvantil
Keďže máme normálne rozdelenie s neznámou varianciou, musíme zistiť t-kvantil. Použite funkciu Excelu =T.INV.2T() uvádzajúci alfa-úrovne (0,08) a stupne voľnosti (n-1). V tomto prípade by to malo dať t-hodnotu 1,8.
Krok 8: Vypočítať dolnú hranicu dôveryhodnostného intervalu
Teraz vypočítajte dolnú hranicu dôveryhodnostného intervalu. Vzorec znie: = Priemer - (t-hodnota * Sigma). Tým sa dostanete k dolnej hranici, ktorá v našom príklade predstavuje 351 eur.
Krok 9: Vypočítať hornú hranicu dôveryhodnostného intervalu
Teraz môžete vypočítať hornú hranicu dôveryhodnostného intervalu. Vzorec je podobný, iba tentoraz pridáte k vašemu priemeru t-hodnotu: = Priemer + (t-hodnota * Sigma). Tak sa horná hranica dostane na 374 eur.
Krok 10: Vizualizácia dôveryhodnostného intervalu
Pre zobrazenie výsledkov môžete v Exceli vytvoriť histogram a na ňom zvýrazniť dôveryhodnostný interval. Nakreslite čiaru medzi spodnou a hornou hranicou, aby ste ukázali, v akej oblasti sa skutočný priemerný obrat bežných zákazníkov s pravdepodobnosťou 92 % nachádza.
Krok 11: Interpretácia a záver
Môžeš teraz zaznamenať, že s istotou 92% skutočný priemer obratu bežného zákazníka leží medzi 351 a 374 eurami. Toto je dôležité pre ďalšie rozhodnutia vo tvojej firme.
Zhrnutie
V tejto príručke si sa naučil/a, ako v Exceli vypočítať oboustranný interval spoľahlivosti pre priemerý obrat. Prešiel/a si všetky potrebné kroky, od prípravy dát po grafické znázornenie a interpretáciu výsledkov.


