Analiza kontigencev v Excelu: Razumevanje povezav

Ko se ukvarjaš z analizo podatkov, boš kmalu naletel na potrebo po prepoznavanju povezav med različnimi spremenljivkami. V tem vodiču ti bom pokazal, kako izvesti kontingenčno analizo v Excelu , da kvantificiraš odnos med dvema nominalnima spremenljivkama. Za to bomo uporabili praktičen primer iz avtomobilske industrije, da bomo razumeli, kako iz podatkov pridobiti dragocene ugotovitve.

Najpomembnejše ugotovitve

• Kontingenčna analiza omogoča preučevanje povezav med dvema nominalnima spremenljivkama.
• Kontingenčni koeficient kvantificira moč odnosa.
• Pivotska tabela v Excelu je nepogrešljivo orodje za analizo.

Korak-za-korak navodila za kontingenčno analizo

Korak 1: Priprava podatkov

Preden začneš s kontingenčno analizo v Excelu, moraš poskrbeti, da so podatki, s katerimi deluješ, pravilno pripravljeni. Odstrani vse filtre, da zagotoviš celoten pregled podatkov.

Ustvari pregled, ki vključuje vodjo proizvodnje in informacije o odklonu kot nominalne podatke. V našem primeru se osredotočamo na vodje izmen A, B in C ter izključimo vse druge zastopnike.

Korak 2: Ustvari pivotsko tabelo

Za izvajanje kontingenčne analize moraš ustvariti dvodimenzionalno porazdelitev frekvenc, ki ti bo pokazala, kako pogosto se pojavi vsaka kombinacija vodje proizvodnje in odklona. V menijski vrstici pojdii na "Vstavljanje" in izberi "Pivotska tabela".

Izberi ustrezno območje podatkov in potrdi, da so naslovi pravilno prepoznani. Tvoja pivotska tabela bo zdaj ustvarjena in lahko primerjaš polja za vodjo proizvodnje in odklon.

Korak 3: Analiza frekvenc

Po ustvarjanju pivotske tabele lahko določiš absolutne frekvence. Postavi značilnosti v vrstice in stolpce pivotske tabele. To ti bo pokazalo, koliko odklonov se je pojavilo na vodjo izmene.

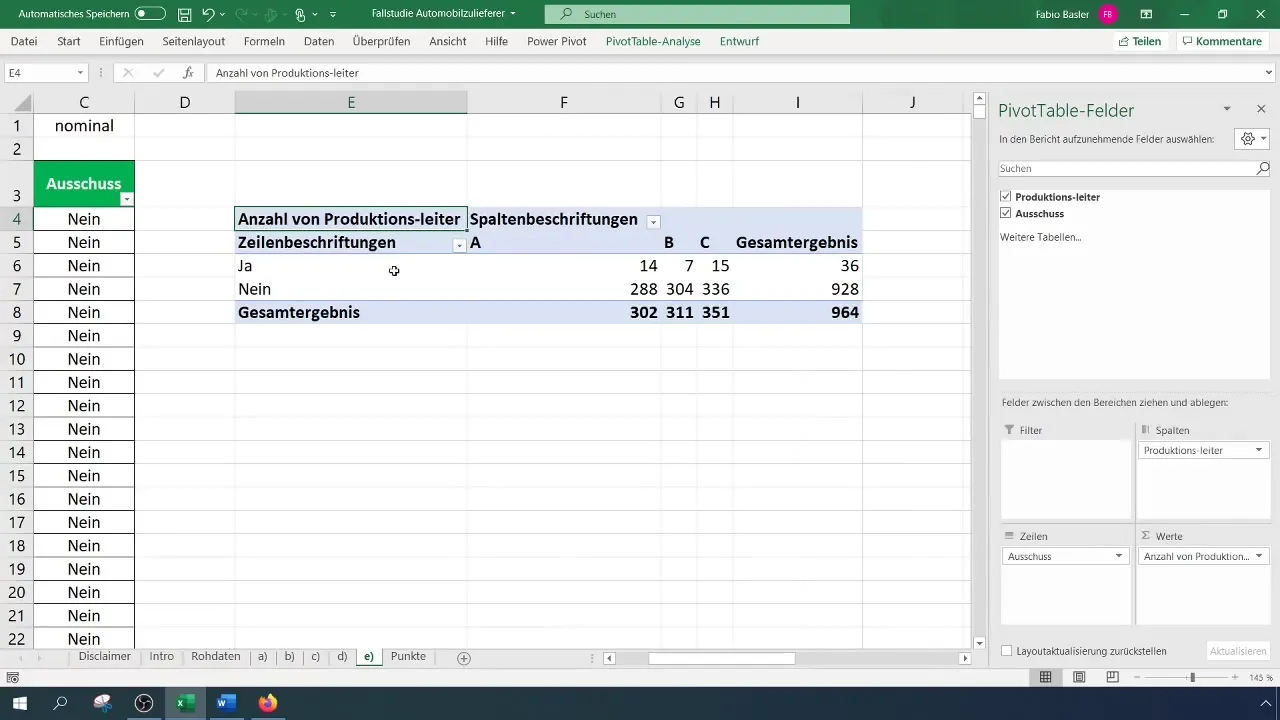
Pogledaj pivotsko tabelo in analiziraj rezultate. Posebej bodi pozoren na porazdelitev spremenljivk, da ugotoviš, pri katerem vodji izmene je odklon najpogostejši ali najredkejši.

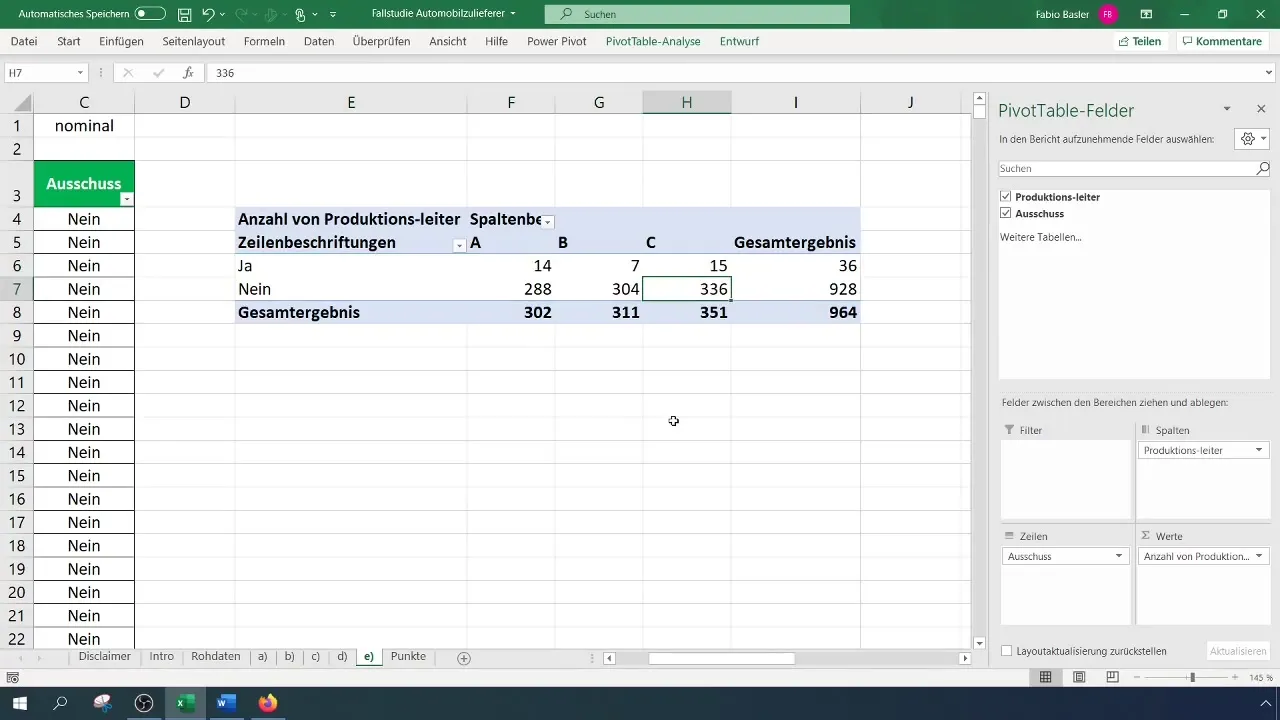
Korak 4: Izračunaj pričakovane frekvence

Za izračun kontingenčnega koeficienta moraš določiti pričakovane absolutne frekvence. Splošna formula pravi: (N_{ij} = \frac{(R_i \times C_j)}{N}), kjer (R) predstavlja stolpčevo frekvenco vrstic in (C) stolpčevo frekvenco stolpcev.

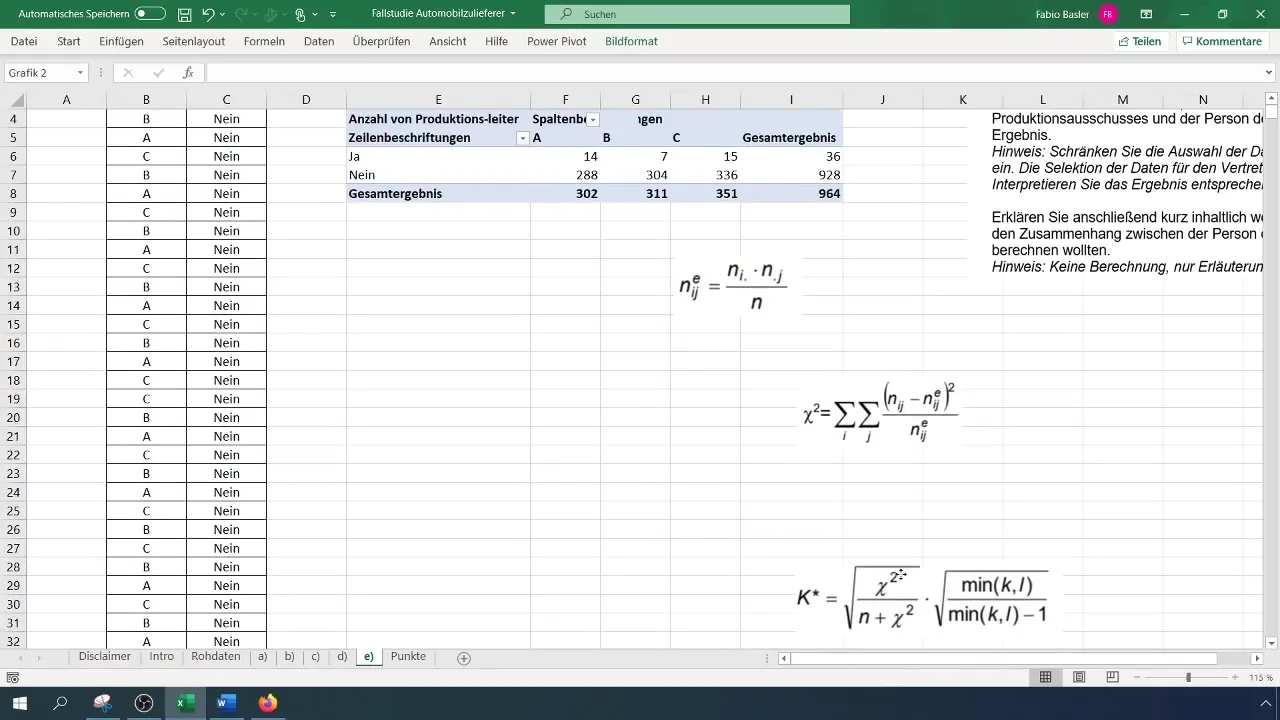
Uporabi ta izračun v vrednostih svoje pivotske tabele. Pri tem bodi pozoren, da ustvariš ločeno tabelo za pričakovane frekvence, da ohraniš preglednost analiz.

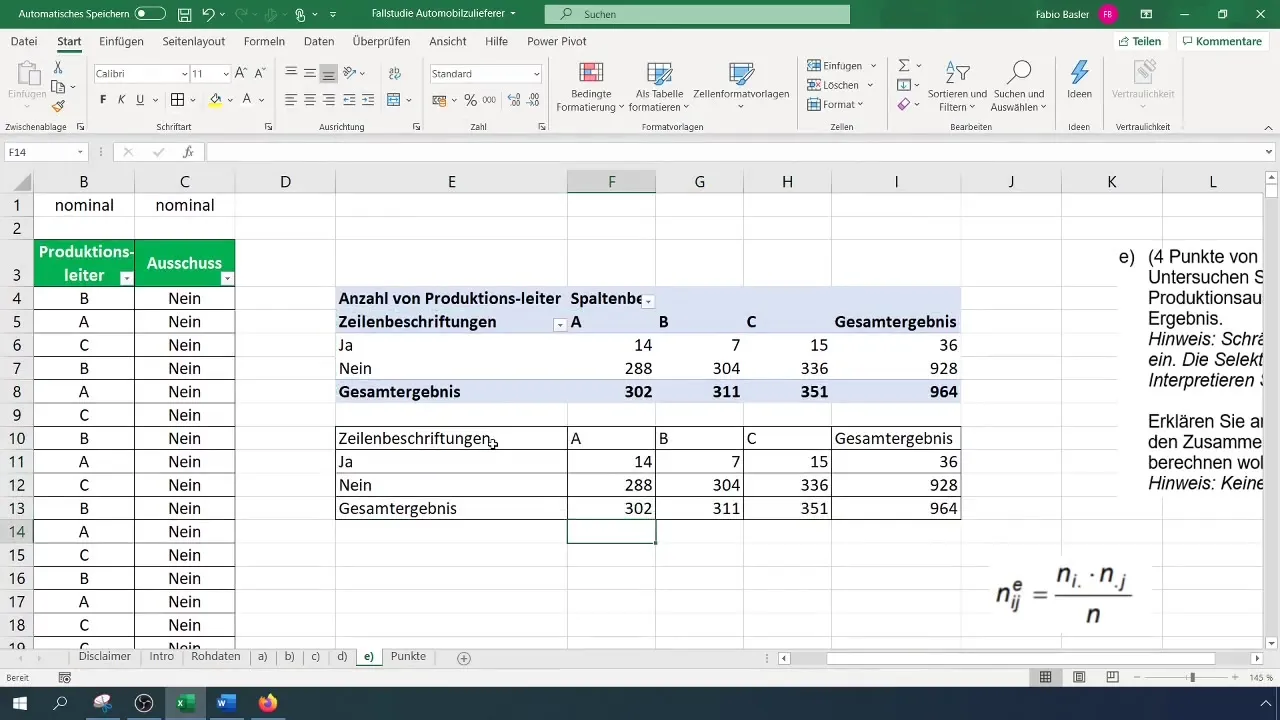
Korak 5: Izračunaj vrednost hi-kvadrat

Zdaj izračunaj vrednost hi-kvadrat, da kvantitativno zajameš odnos med spremenljivkami. Formula pravi:

[ \chi^2 = \sum \frac{(O{ij} - E{ij})^2}{E_{ij}} ]

Tukaj je (O) opažena frekvenca in (E) pričakovana frekvenca.

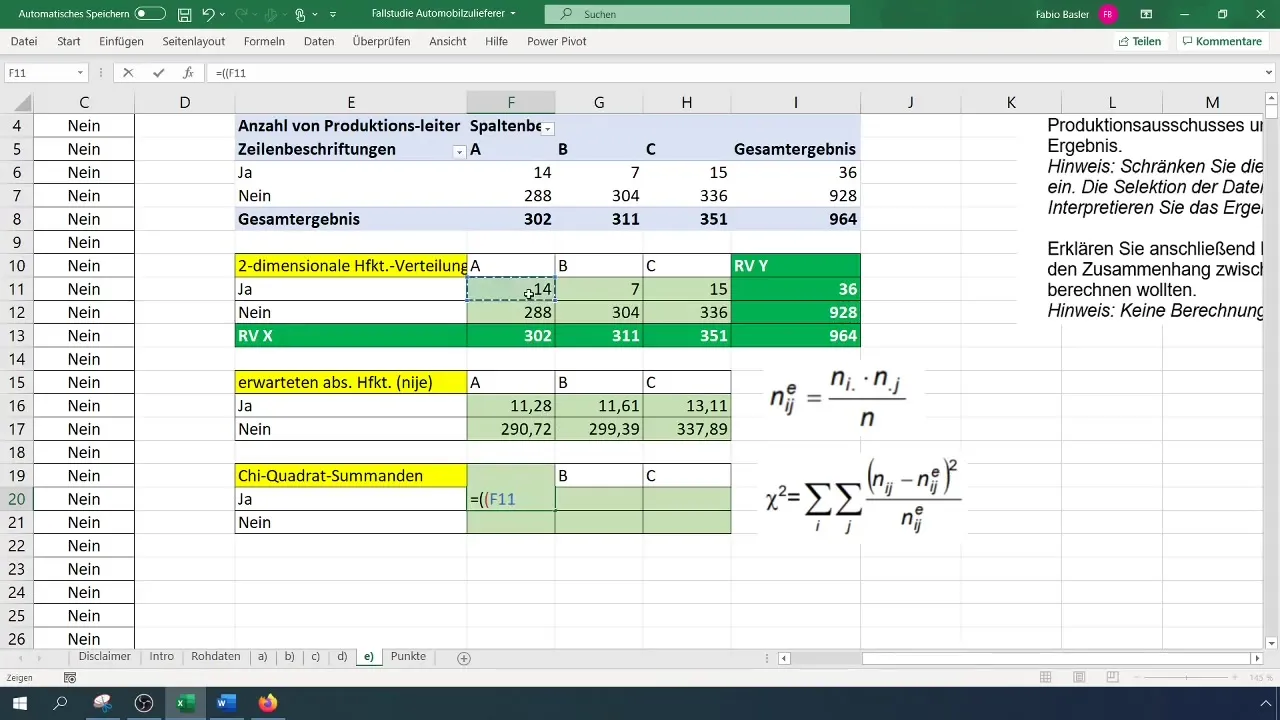
Izračunaj razlike med opaženimi in pričakovanimi frekvencami ter jih kvadriraj.

Korak 6: Izračun kontingenčnega koeficienta

Zadnji korak je izračun kontingenčnega koeficienta. Formula za izračun je:

[ K = \sqrt{\frac{\chi^2}{N}} ]

Uporabi prej izračunano vrednost hi-kvadrata in skupno število opazovanj (N).

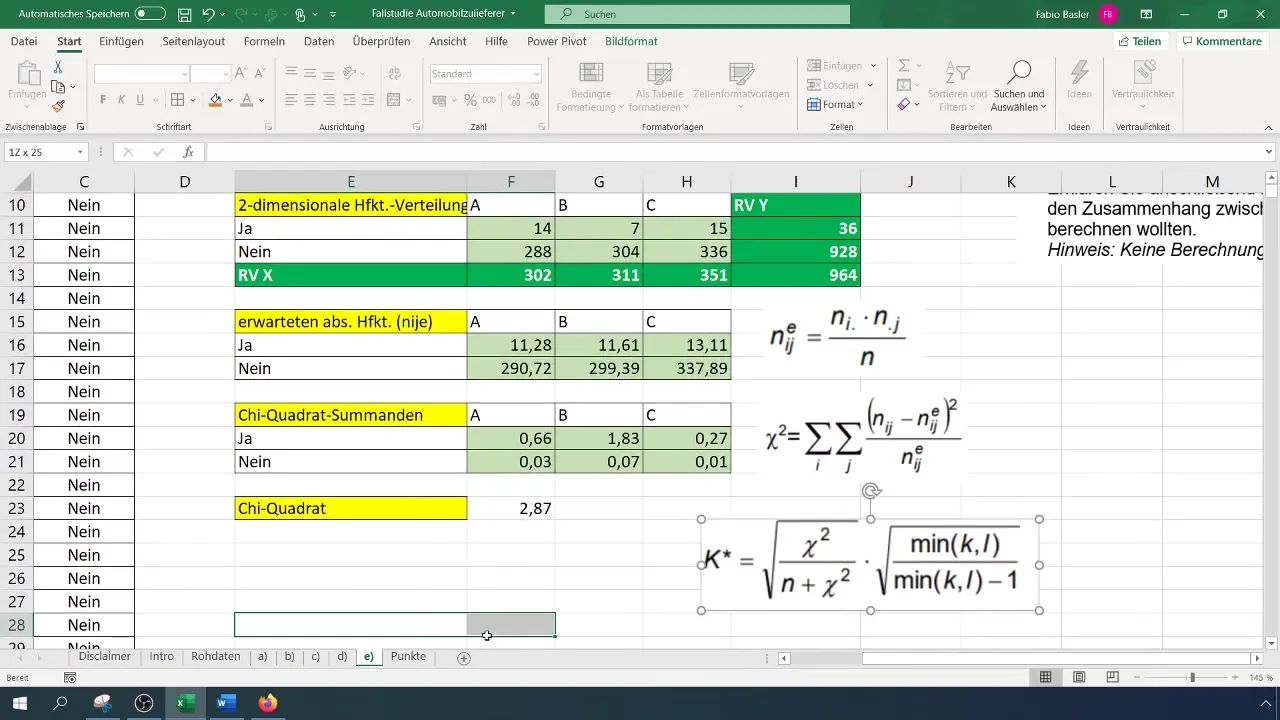
Ko izračunate kontingenčni koeficient, lahko interpretirate rezultat. Naša analiza je pokazala, da kontingenčni koeficient 0,077 kaže na šibko povezavo med spremenljivkami.

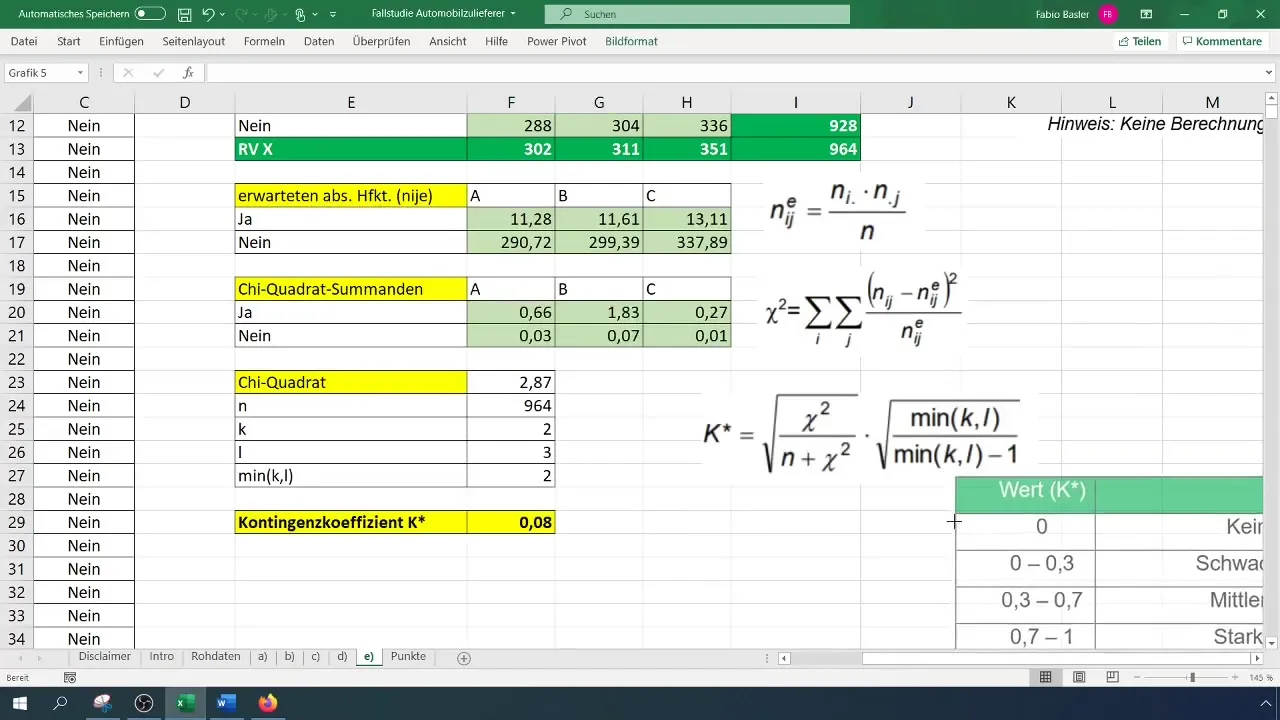
Korak 7: Interpretacija rezultatov

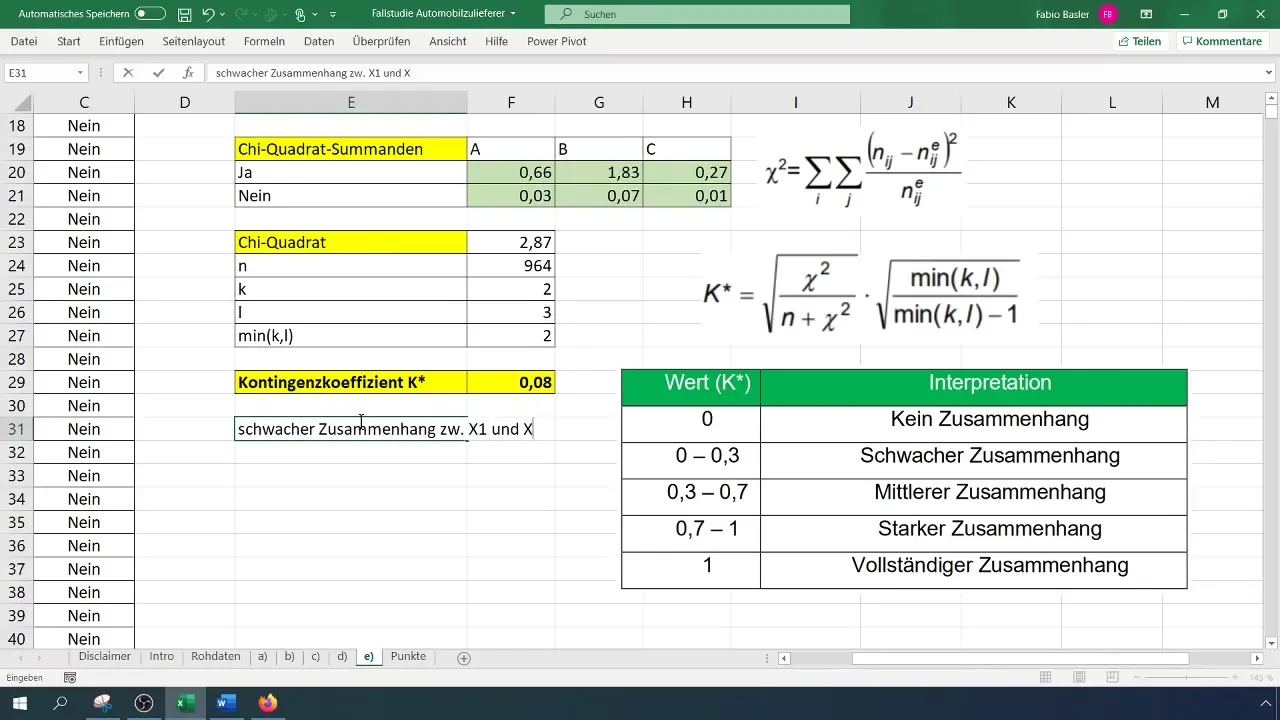
Zadnji koraki analize vključujejo interpretacijo rezultatov. Kontingenčni koeficient blizu 0 kaže, da skorajda ni povezave med spremenljivkami. Vrednost 0,08 nakazuje, da proizvodni vodja nima pomembnega vpliva na pojav reklamacij.

Povzetek

V tej vadnici ste izvedeli, kako izvesti kontingenčno analizo v Excelu za odkrivanje povezav med nominalnimi spremenljivkami. Naučili ste se, kako pripraviti podatke, ustvariti pivotno tabelo in opraviti potrebne izračune za kontingenčni koeficient.