Uspešno testiranje pričakovane vrednosti v Excelu z uporabo 1-SP

Statistična testiranja so ključni del analize podatkov in odločanja. Še posebej v biotehnološkem sektorju je lahko ključno preverjanje hipotez o uspešnosti aktivnih snovi. V okviru tega vadnice se boste naučili, kako učinkovito izvesti enostaven test vzorca (1-SP-Test) za pričakovano vrednost z znano varianco v Excelu.

Najpomembnejše ugotovitve

Ta vodnik vam bo posredoval:

• Teoretične osnove 1-SP-Testa.
• Korake za izvedbo testa v Excelu.
• Interpretacija rezultatov.

Priprava podatkov

Za izvedbo 1-SP-Testa v Excelu najprej potrebujete ustrezne podatke. V našem primeru bomo izhajali iz situacije, ko analizirate uspešnost aktivnih snovi. Znano je, da je bila povprečna uspešnost prej 59%, pri standardnem odklonu 19. Najprej svoje podatke vnesite v Excelovo preglednico.

Pazite, da so vaši podatki organizirani v stolpce, da nanje lahko pozneje dostopate. Jasno urejenost vam bo olajšalo sledenje posameznim korakom.

Pregled testa

1-SP-Test služi preverjanju, ali se povprečna vrednost uspeha bistveno razlikuje od predhodno določene vrednosti. V tem primeru preverjamo, ali se lahko v prihodnosti uspešnost 59% znatno poveča.

Postavitev hipotez

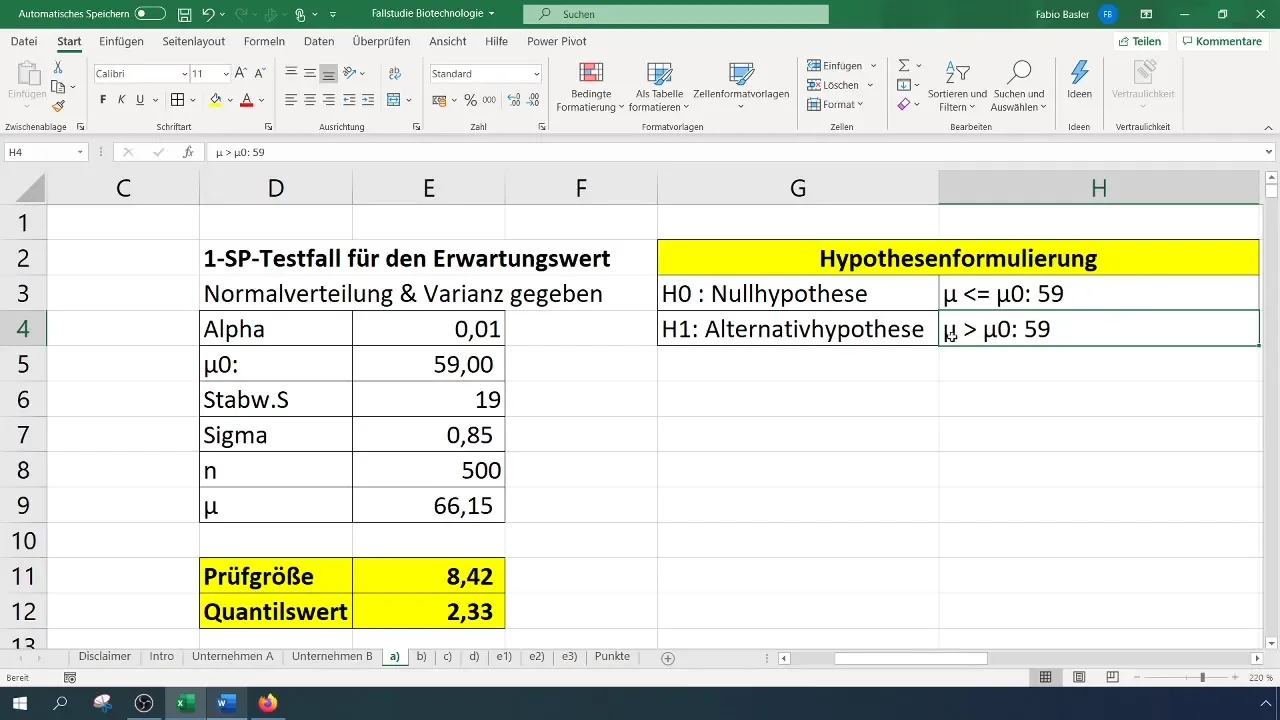
Postavljene hipoteze za test so ključnega pomena:

• Nullhipoteza (H0): Prava pričakovana vrednost je enaka 59 (σ = 59%).
• Alternativna hipoteza (H1): Prava pričakovana vrednost je večja od 59%.

Pri postavljanju hipotez se osredotočite na to, kaj natančno morate preizkusiti in kako se to odraža v vašem kontekstu.

Pomembno je jasno razlikovanje med nullhipotezo in alternativno hipotezo, saj predstavljata osnovo za nadaljnje izračune.

Zajem vzorca

Za naš test vzamemo vzorec 500 aktivnih snovi. Pomembno je upoštevati, da je izbira vzorca reprezentativna in bi s primernim pristopom morala zagotoviti, da se vaši rezultati lahko realistično preslikajo na celotno populacijo.

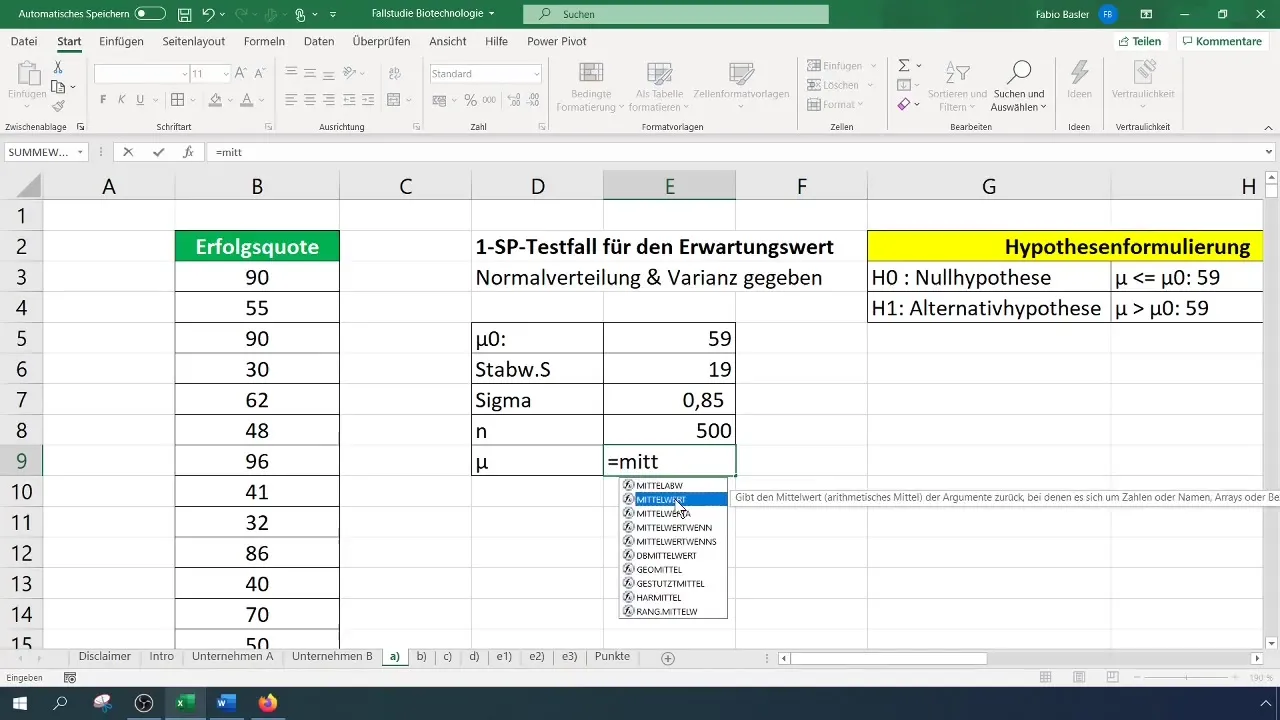
Za test najprej izračunate aritmetično sredino. To naj bi enostavno izvedete tako, da v Excelu uporabite ustrezno formulo.

Izračun preizkusne velikosti

Preizkusna velikost za 1-SP-Test se določi s sledečo formulo:

[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]

Tukaj je (\bar{x}) srednja vrednost vašega vzorca, (\mu_0) predpostavljena srednja vrednost (v tem primeru 59), (\sigma) standardni odklon (v tem primeru 19), in (n) število vzorcev (500).

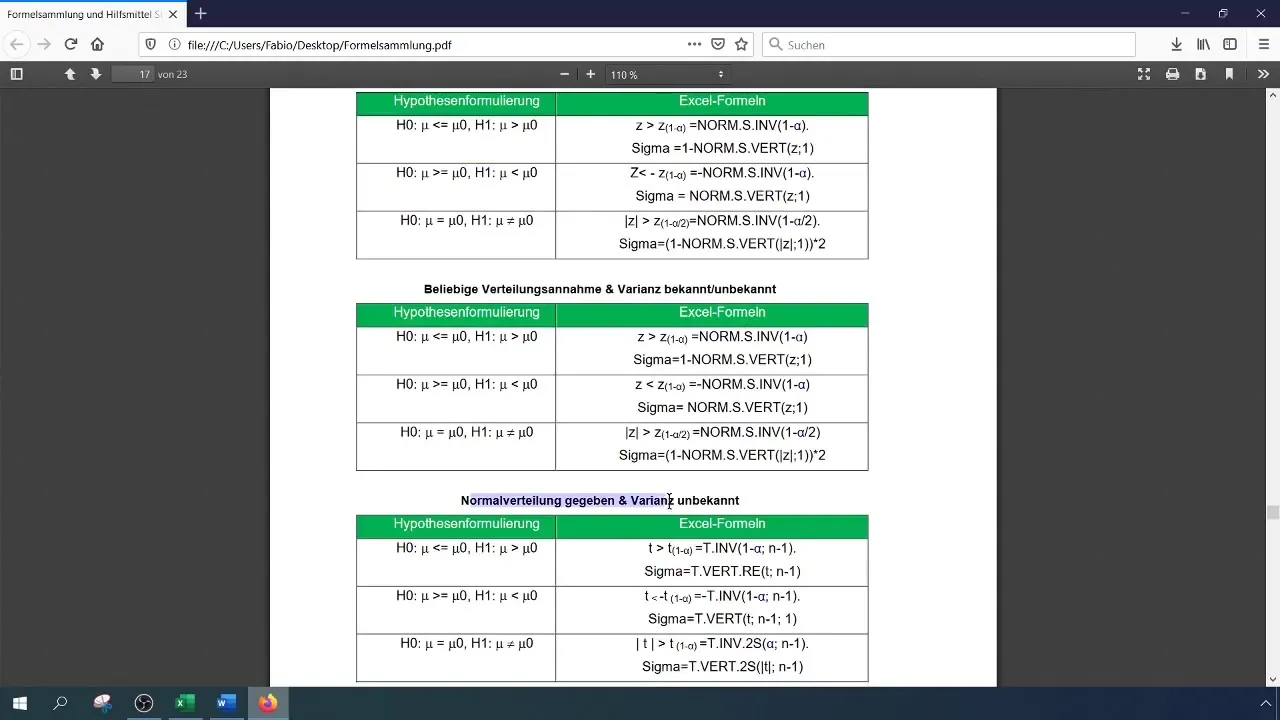
Po vstavitvi vrednosti v formulo izračunajte preizkusno velikost, da ugotovite, ali je pomembna ali ne.

Določitev kritične vrednosti

Za stopnjo pomembnosti 1% (0,01) morate prebrati ali izračunati kritično vrednost. To lahko storite v Excelu s funkcijo NORM.S.INV.

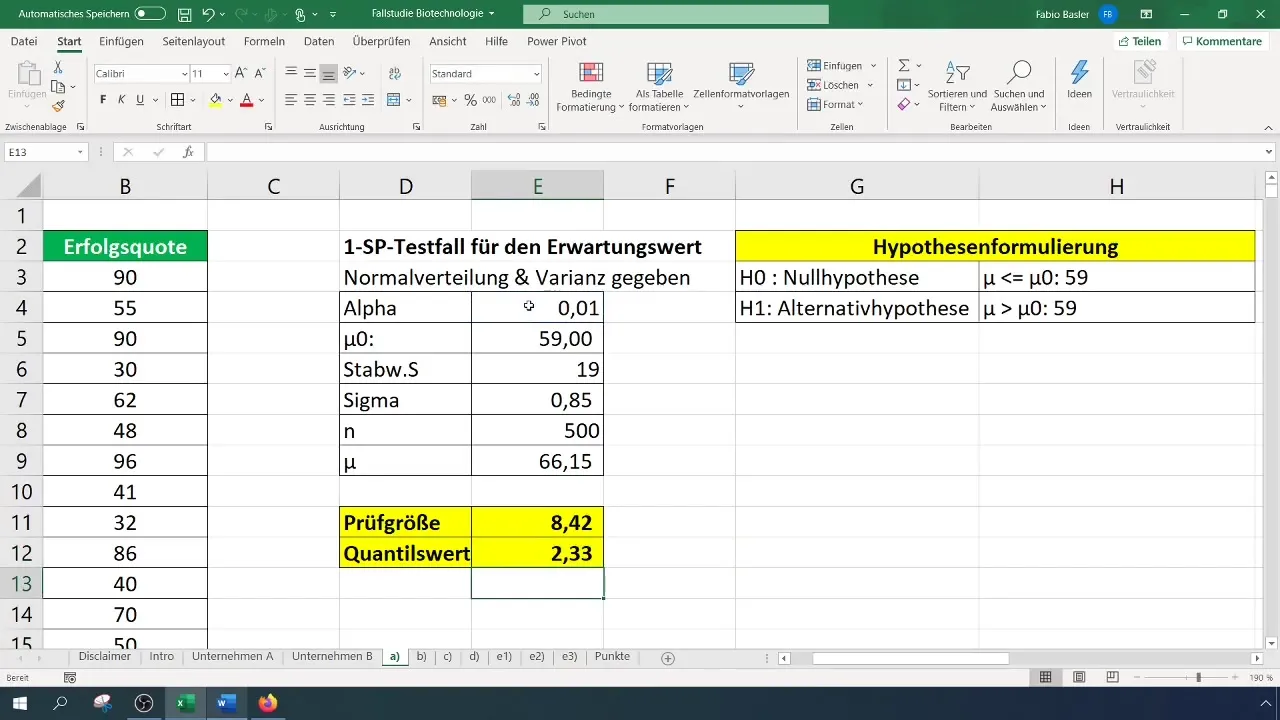
Formula je:

[ \text{NORM.S.INV}(1 - \alpha) ]

Tukaj je (\alpha) stopnja pomembnosti (0,01). Dobljena vrednost bo osnova za primerjavo s preizkusno velikostjo.

Izvedba testa

Po tem, ko imate tako preizkusno velikost kot tudi kritično vrednost, ju primerjate:

• Če je preizkusna velikost večja od kritične vrednosti, se nullhipoteza zavrne.
• V nasprotnem primeru nullhipoteze ni mogoče zavrniti.

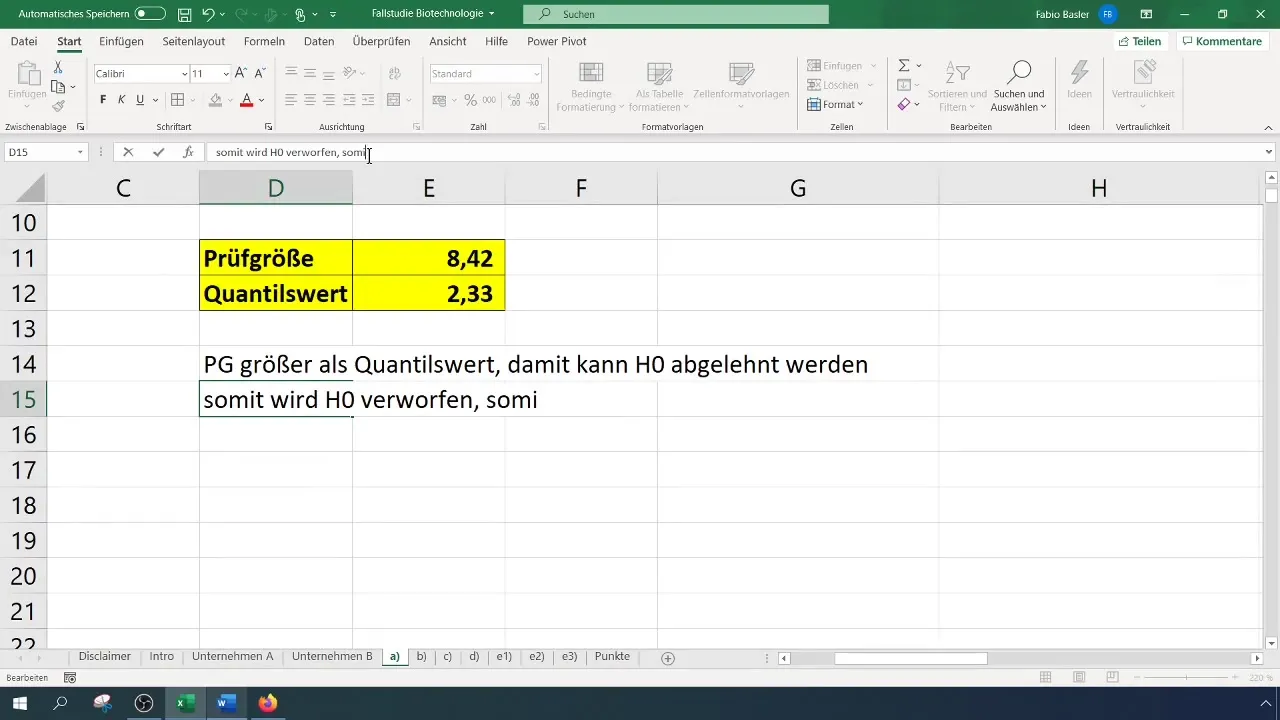
V našem primeru je bil testni rezultat 8,4, kar presega kritično vrednost 2,33. Zato lahko zavrnemo ničelno hipotezo. To kaže, da se je stopnja uspeha pomembno izboljšala.

Interpretacija rezultatov

Po opravljenem testu in ugotovljenih rezultatih jih morate jasno interpretirati v določenem kontekstu. Zavrnitev ničelne hipoteze pomeni, da se preizkušena nova vrednost pomembno razlikuje od preteklosti, v tem primeru 59 %.

Te informacije so izjemno pomembne za strateško odločanje v vašem podjetju. Potrjujejo, da so bili napori za izboljšanje stopnje uspeha učinkoviti.

Povzetek

V tem vadnem programu ste se naučili, kako izvesti 1-SP-test za pričakovano vrednost v Excelu. Na podlagi študijskega primera ste lahko sledili korakom od postavljanja hipotez do izračuna podatkov in interpretacije rezultatov. Ta znanja so ne le dragocena za znanstvene analize, temveč tudi za praktične aplikacije v podjetju.