Test prilagajanja Chi-kvadrata predstavlja preprosto metodo za preverjanje hipoteze, ali dani niz podatkov sledi normalni porazdelitvi. V tej vadnici se boš naučil, kako izvesti test Chi-kvadrat v Excelu, da ugotoviš, ali prihodki pametnih telefonov sledijo normalni porazdelitvi. Korak za korakom bomo sledili postopku, ki sega od izdelave razvrščene frekvenčne tabele do izračuna testne velikosti in primerjave s kritično vrednostjo Chi-kvadrata.
Najpomembnejša spoznanja
- Test prilagajanja Chi-kvadrata pomaga pri preverjanju normalnih porazdelitev.
- Pomembno je, da ustvariš razvrščeno frekvenčno tabelo.
- Testno velikost primerjaš s kritično vrednostjo, da zavrneš ali sprejmeš ničelno hipotezo.
Korak za korakom vodnik
Korak 1: Priprava podatkov
Za izvedbo testa Chi-kvadrat najprej potrebuješ podatke. Kopiraj prihodke pametnih telefonov v Excelovo delovni list. Prepričaj se, da so tvoji podatki organizirani v eni sami stolpcu.

Korak 2: Ustvarjanje histograma
Za pridobitev prvih vizualnih napotkov o porazdelitvi ustvari histogram svojih podatkov. Pojdi na "Vstavi" in izberi "Grafikone". Dodaj histogram, tako da izbereš območje za podatke.
Korak 3: Ustvarjanje razvrščene frekvenčne tabele
Za test Chi-kvadrat potrebuješ razvrščeno frekvenčno tabelo. Najprej določi število razredov za svojo tabelo – v tem primeru uporabljamo šest razredov. Izračunaj širino intervalov in ustvari tabelo v skladu s tem.
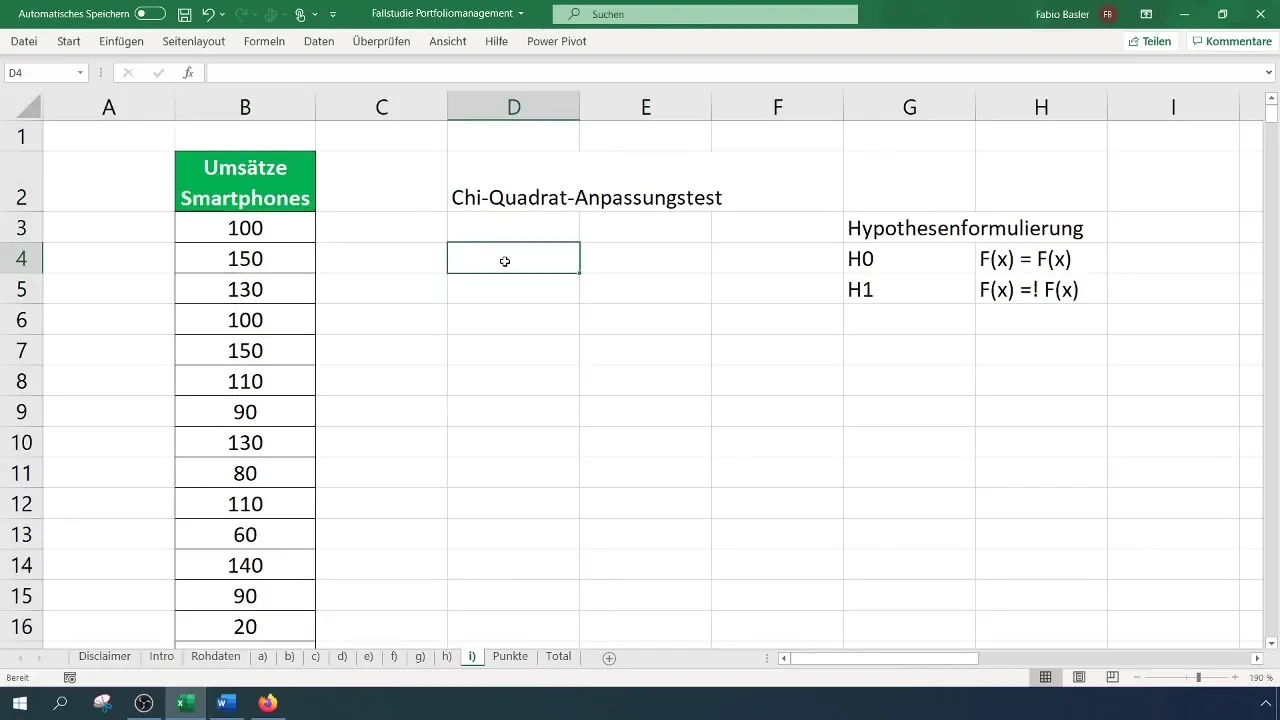
Korak 4: Izračun frekvenc
Zdaj moraš izračunati opažene frekvence za vsak razred. Pojdi na "Analiza podatkov" v meniju in izberi "Histogram". Izberi vnosno območje za svoje podatke in mejne vrednosti razredov. Določi izhodno območje za frekvenčno tabelo.
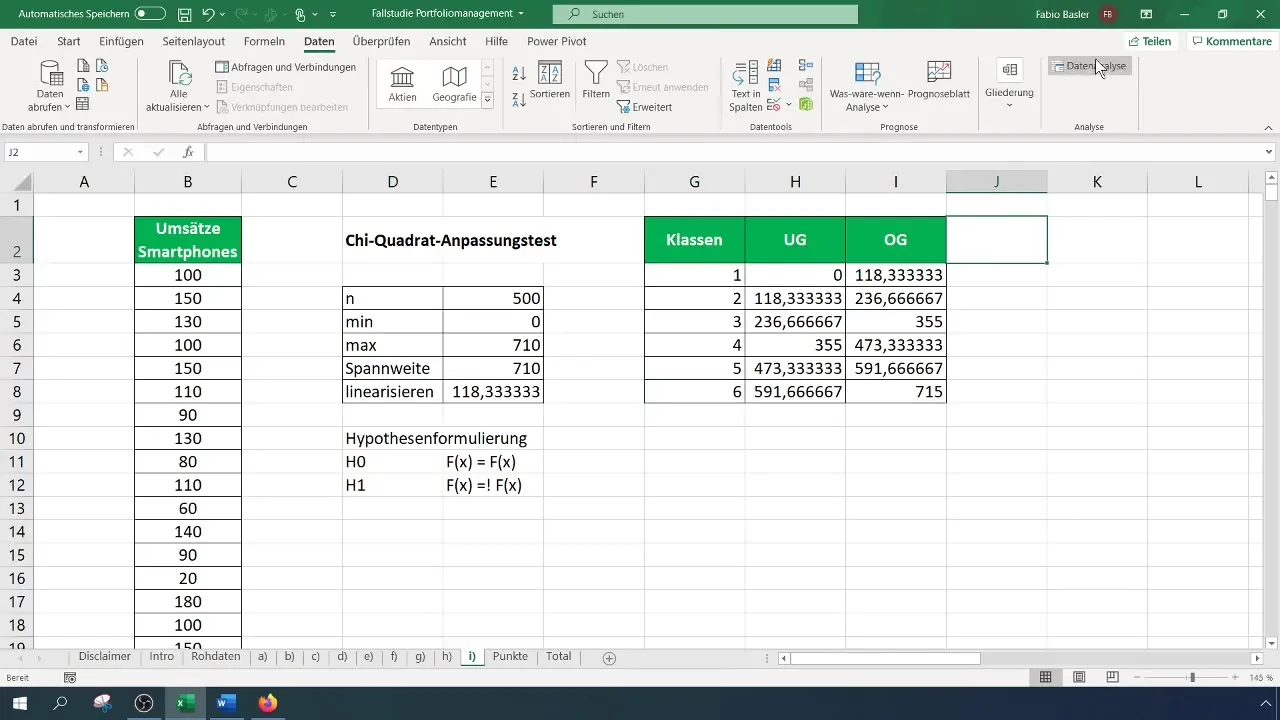
Korak 5: Izračun pričakovanih frekvenc
Za določitev pričakovanih frekvenc izračunaj verjetnosti za vsak razred na podlagi predpostavljene normalne porazdelitve. Za to potrebuješ povprečje in standardni odklon svojih podatkov.
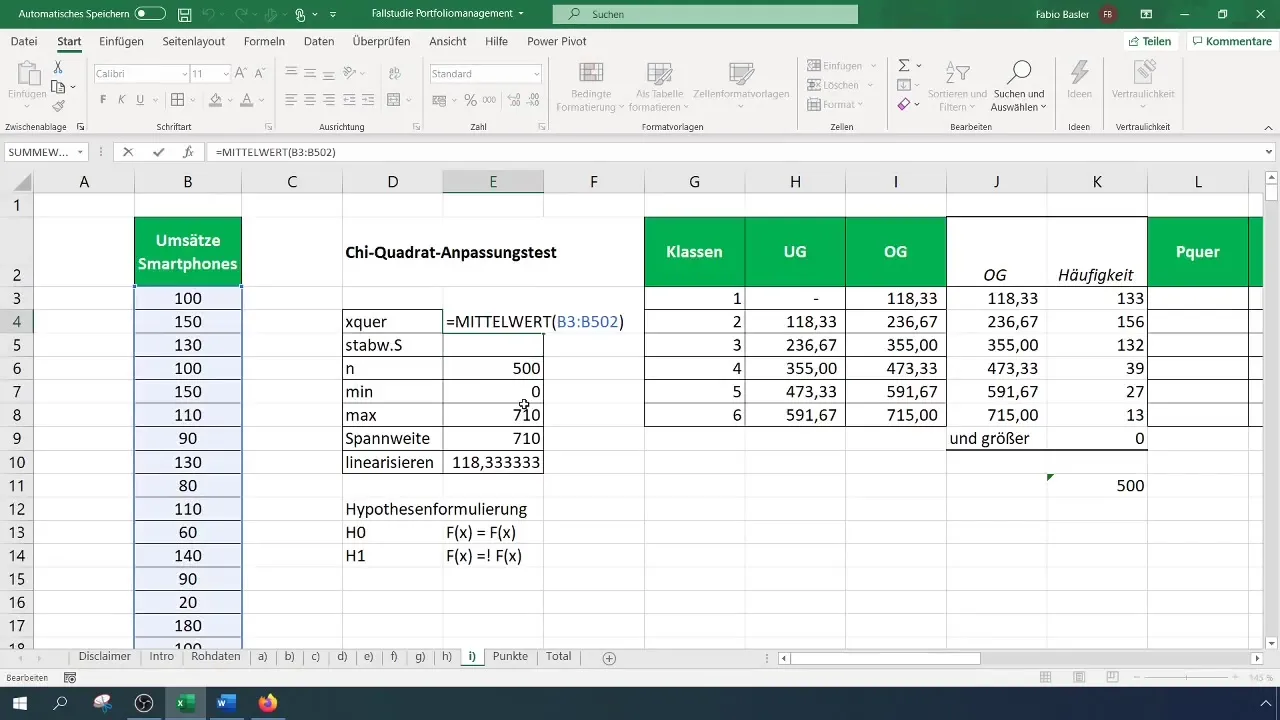
Korak 6: Izračun testne velikosti
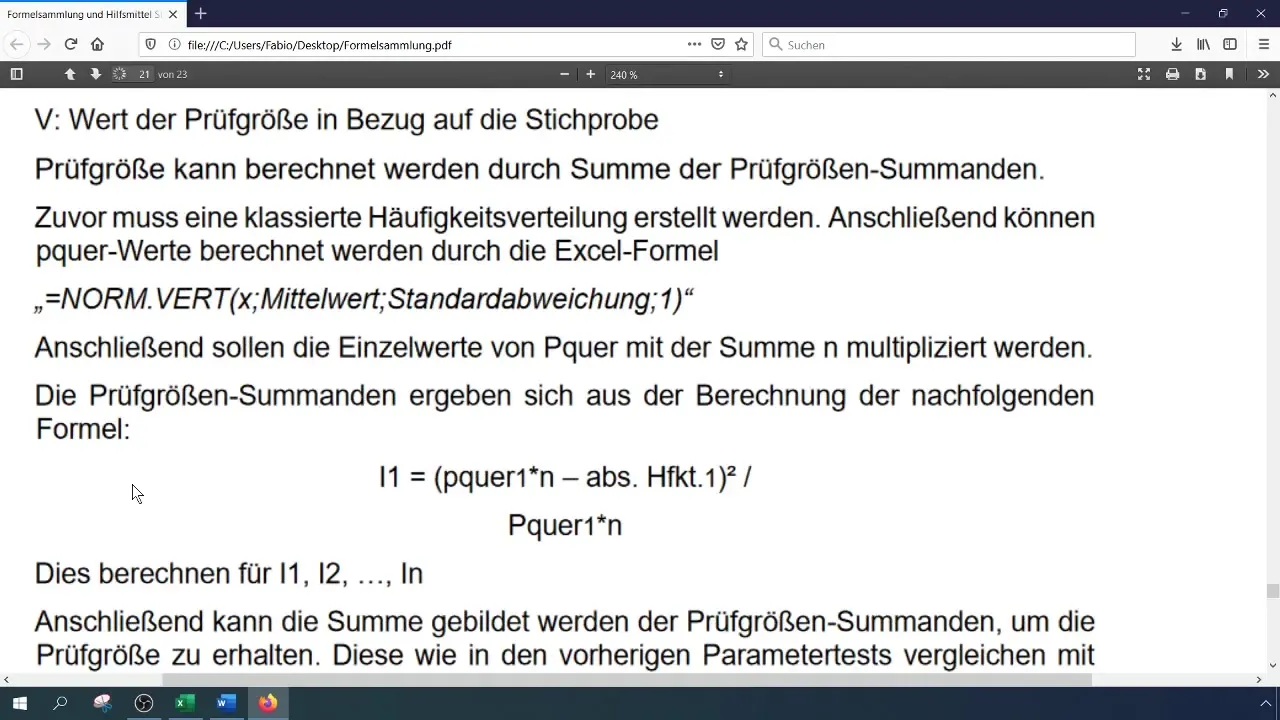
Izračunaj testno velikost (Chi-kvadrat) s formulo:
[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]
kjer sta (O_i) opažene in (E_i) pričakovane frekvence. Ta izračun lahko izvedeš v Excelu, tako da shraniš posamezne komponente v ločenih celicah.
Korak 7: Izračun kritične vrednosti
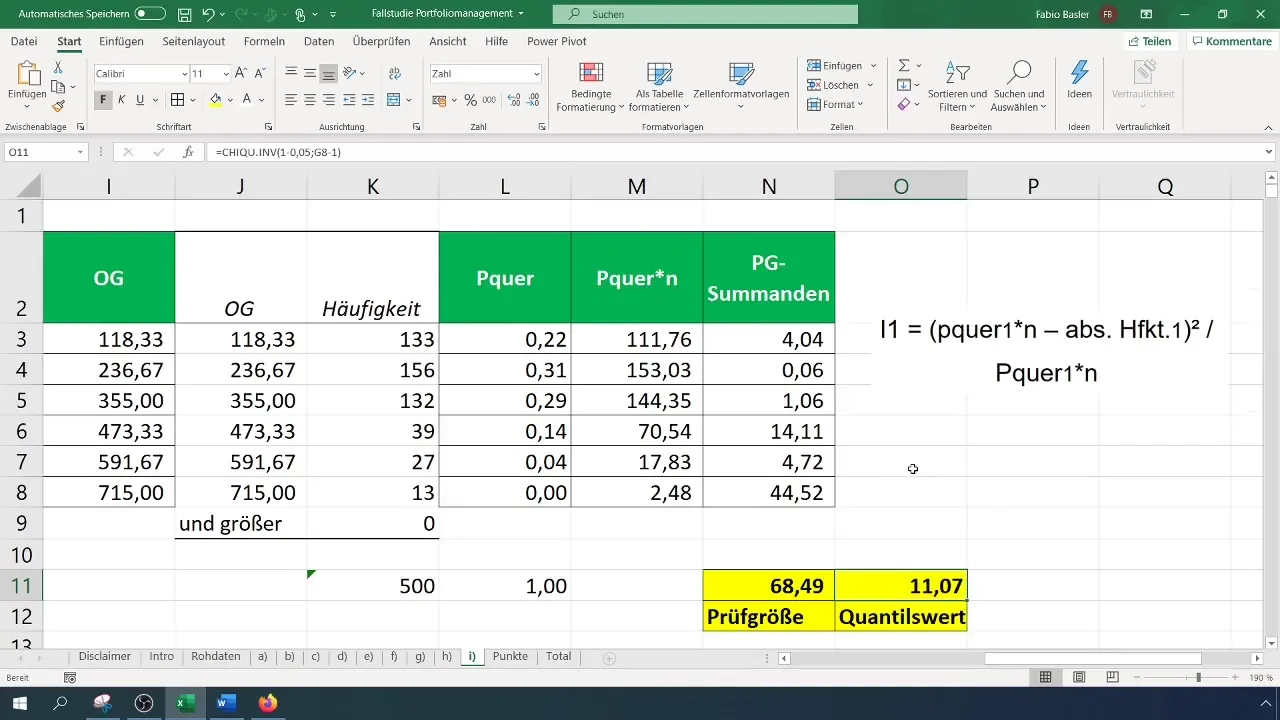
Za oceno testne velikosti moraš izračunati kritično vrednost (\chi^2) za tvojo stopnjo zaupanja in število prostostnih stopenj. Število prostostnih stopenj za test Chi-kvadrat je (k - 1), kjer je (k) število razredov.
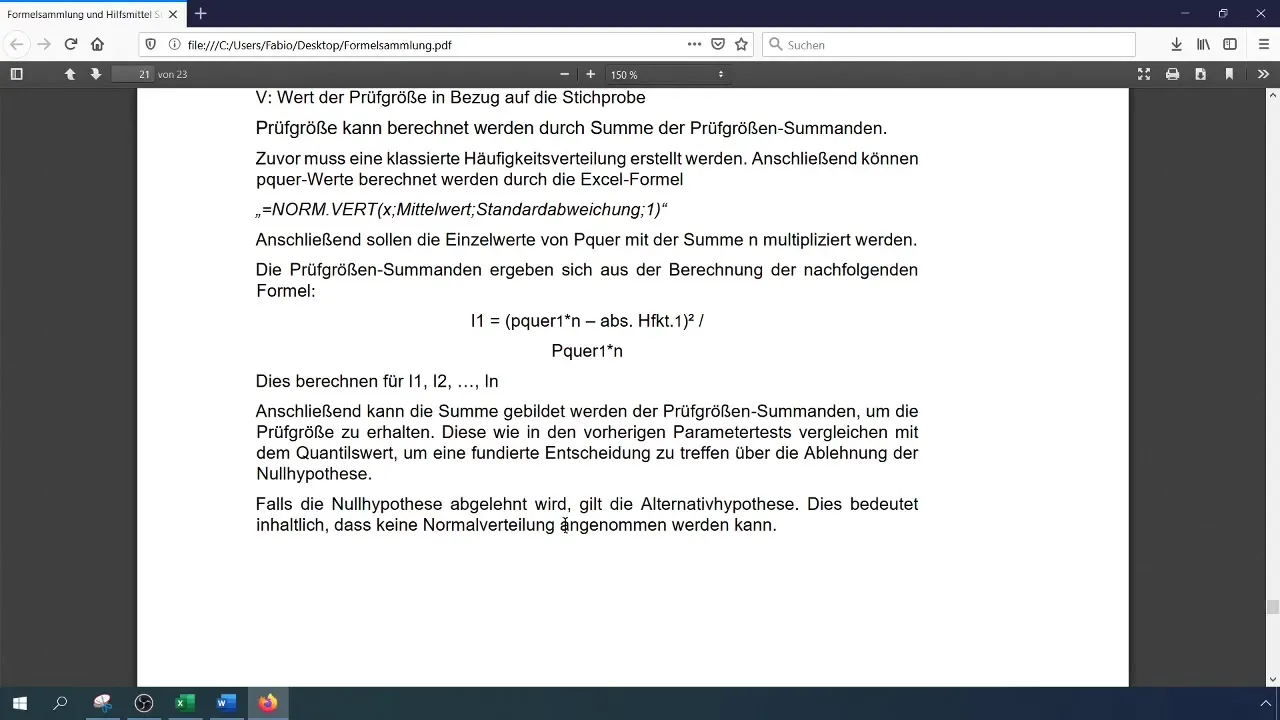
Korak 8: Preverjanje hipotez
Primerjaj izračunano testno velikost s kritično vrednostjo. Če je testna velikost večja od kritične vrednosti, zavrni ničelno hipotezo, kar pomeni, da podatki niso normalno porazdeljeni. V nasprotnem primeru sprejmi ničelno hipotezo.
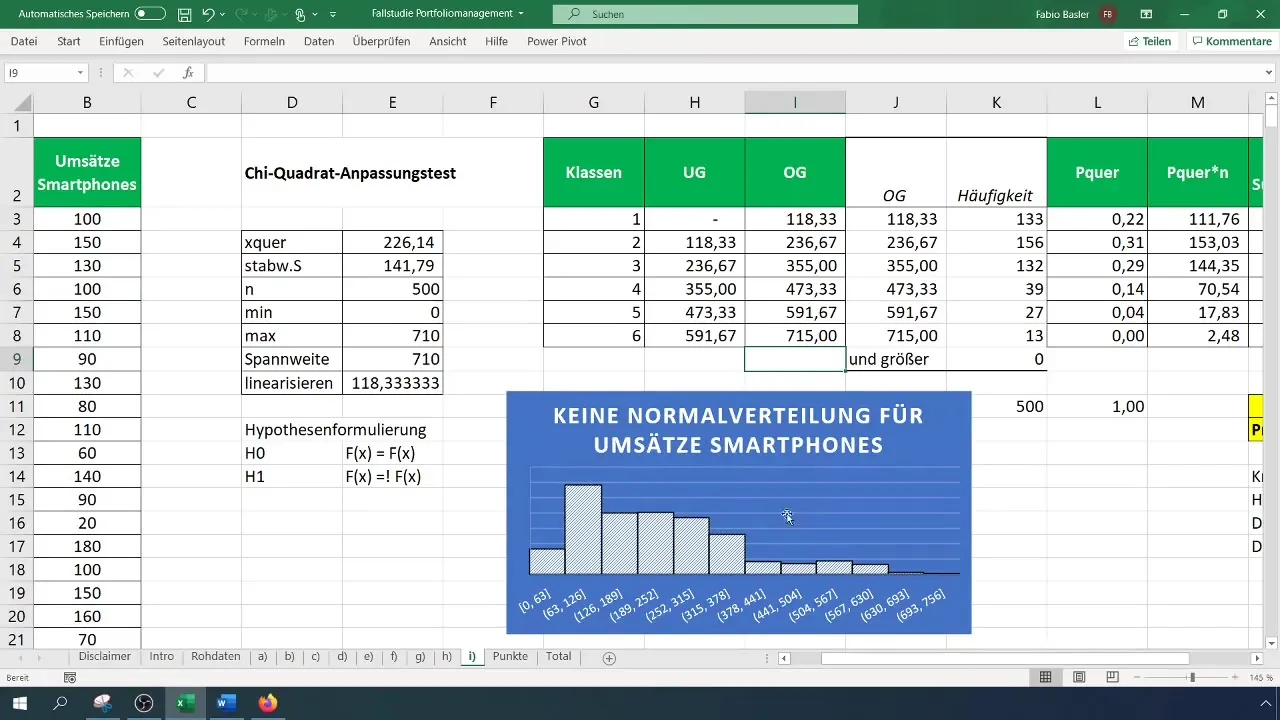
Korak 9: Povzetek rezultatov
Zabeležite svoje rezultate in jih razširite z grafičnimi podatki ter preizkusi hipotez. Ne pozabite preveriti svojega histograma, da vizualno potrdite, da porazdelitev ni normalna.
Povzetek
V procesu tega vodiča ste se naučili, kako izvesti test prilagajanja hi-kvadrata v Excelu, da analizirate normalno porazdelitev svojih prihodkov s pametnih telefonov. Koraki vključujejo ustvarjanje razvrščene frekvenčne tabele, izračune za pričakovane frekvence, testno statistiko in končno primerjavo s kritično vrednostjo.
Pogosta vprašanja
Kaj je test prilagajanja hi-kvadrata?Test prilagajanja hi-kvadrata preverja, ali opažena frekvenčna porazdelitev ustreza normalni porazdelitvi.
Koliko razredov potrebujem za frekvenčno tabelo?Običajno je smiselno imeti vsaj 5 do 10 razredov, da lahko podatke ustrezno analiziramo.
Kaj storiti, če je zavrnjena ničelna hipoteza?Če zavrnemo ničelno hipotezo, to pomeni, da podatki niso normalno porazdeljeni.
Kako izračunati kritično vrednost hi-kvadrata?Kritično vrednost preberemo iz tabele hi-kvadrata na podlagi prostostnih stopenj in zaželenega ravni značilnosti.


