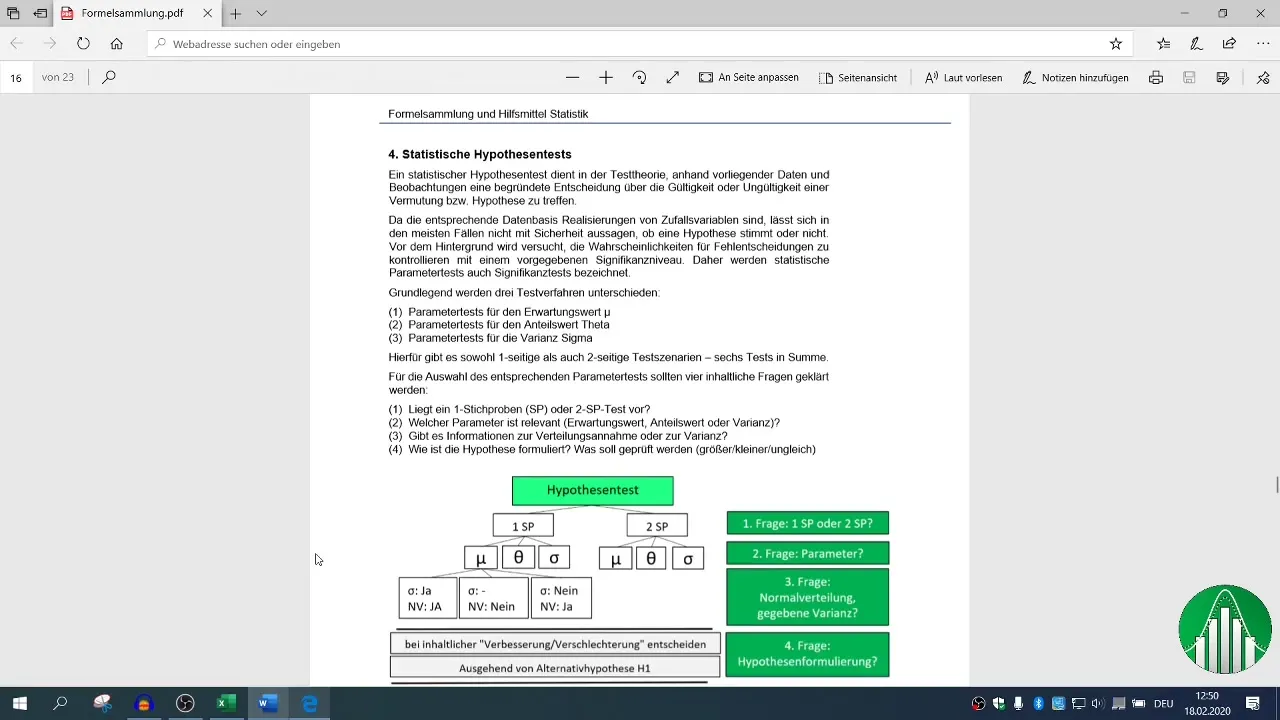
Statistični preizkusi hipotez so pomembno orodje za sprejemanje odločitev na podlagi podatkov. V tem vadnici se boš naučil, kako izvesti 1-vzorčni preizkus za pričakovano vrednost v Excelu, da boš določil, ali se je povprečni promet podjetja izboljšal po uvedbi spremenljivega nagrajevanja. Z uporabo te metode boš sposoben sprejemati odločitve na podlagi podatkov in pridobiti dragocene vpoglede v uspešnost svojega podjetja.
Najpomembnejše ugotovitve
- Naučil se boš, kako oblikovati in preverjati hipoteze.
- Izvajanje preizkusa poteka v Excelu z uporabo statističnih formul.
- Interpretacija rezultatov omogoča utemeljene odločitve o povečanju prometa.
Korak za korakom vodnik
Korak 1: Zbiranje in priprava podatkov
Imaš dostop do naključnega vzorčenja, ki zajema povprečne tedenske prihodke v obsegu 100 tednov. Ti podatki so osnova za tvoj preizkus. Začni z vnašanjem relevantnih informacij v Excelovo delovno preglednico.

Korak 2: Določitev hipotez
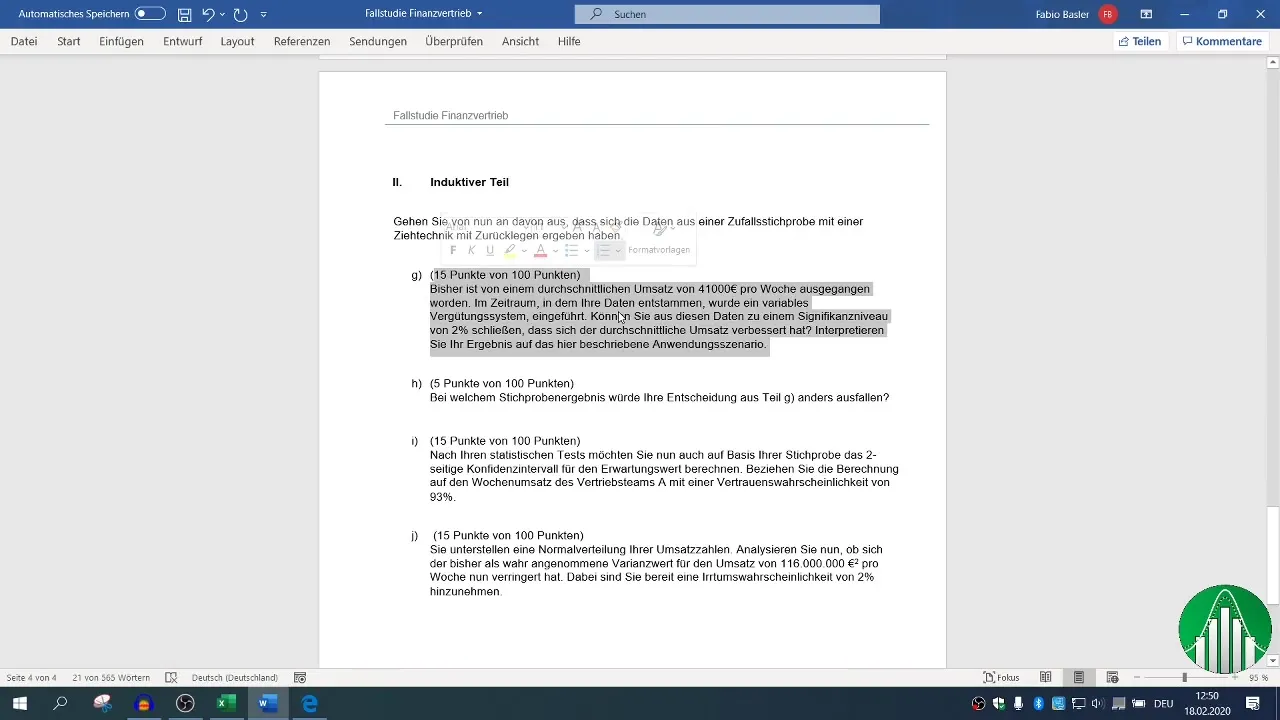
Oblikuj ničelno hipotezo (H0) in alternativno hipotezo (H1). V tvojem primeru ničelna hipoteza trdi, da je povprečni promet enak ali manjši od 41.000 € (m ≤ 41.000). Alternativna hipoteza pa pravi, da je povprečni promet večji od 41.000 € (m > 41.000).
Korak 3: Izračun srednje vrednosti in standardnega odklona
Izračunaj srednjo vrednost prihodkov iz tvojega vzorca z uporabo funkcije SREDNJA.VREDNOST v Excelu. Za izračun standardnega odklona uporabi formulo STANDARDNO.OPOZORILO, ker delaš v induktivni statistiki in moraš stopnjo svobode zmanjšati za ena.
Korak 4: Določitev kritične vrednosti
Določi kritično vrednost z uporabo Excelove funkcije NORM.S.INV. V argumentih uporabi 1 - α (0,98). Stopnja značilnosti za tvoj preizkus je 2 %.

Korak 5: Primerjava preizkusne velikosti s kritično vrednostjo
Zdaj primerjaj izračunano preizkusno velikost s kritično vrednostjo z. Če je preizkusna velikost večja od kritičnega z, lahko zavržeš ničelno hipotezo.

Korak 6: Odločitev o hipotezi
Če je preizkusna velikost večja od kritične vrednosti, se zavrne ničelna hipoteza, kar pomeni, da lahko sklepaš, da se je povprečni promet izboljšal. To odločitev dokumentiraj v svojih rezultatih.

Korak 7: Interpretacija rezultatov
Interpretacija rezultatov je ključnega pomena. Pokazal si, da je nova srednja vrednost 46.669 €, kar je več od prejšnje vrednosti 41.000 €. To nakazuje, da se je finančna slika po uvedbi spremenljivega nagrajevanja izboljšala in da obstaja pozitiven vpliv na motivacijo zaposlenih.
Povzetek
V tej vadnici si se naučil, kako izvesti 1-vzorčni preizkus za pričakovano vrednost v Excelu. Od zbiranja podatkov, oblikovanja hipotez, izračuna srednje vrednosti in standardnega odklona do odločanja o hipotezi — vsak korak je bil ključen za pravilno statistično analizo. S tem znanjem lahko sprejemaš utemeljene odločitve v svojem podjetju.
Pogosto zastavljena vprašanja
Kako oblikovati hipoteze?Ničelna hipoteza (H0) predstavlja obstoječe stanje, medtem ko alternativna hipoteza (H1) predpostavlja spremembo.
Kaj pomeni preizkusna velikost v statističnem testu?Preizkusna velikost se uporablja za določanje, ali je mogoče zavrniti ničelno hipotezo.
Kako razlagati primerjavo med preizkusno velikostjo in kritično vrednostjo?Če je preizkusna velikost večja od kritične vrednosti, se ničelna hipoteza zavrne.


