I denna handledning visar jag dig grunderna för att skapa formler för axlarna i Deforum Stable Diffusion. Vi kommer att titta på de grundläggande koncepten som du behöver för att kontrollera kameraaxlarna och deras rörelser. På slutet kommer du att ha en bra förståelse för hur du kan använda matematiska formler för att ge liv åt din animation och uppnå olika kameraeffekter.
Viktigaste insikter
- Formlerna inom parenteserna definierar kamerans rörelse över tiden.
- Du kan använda matematiska funktioner som sinus, cosinus och tangens för att skapa olika kameraanimationer.
- Justeringar av parametrarna i formlerna möjliggör olika svängningar och rörelsemönster för kameran.
Steg för steg guide
Först tittar vi på grunderna för kameraaxlarna. Du bör veta att kameraaxlarna spelar en avgörande roll i en animeringsprocess. Startvärdena i formlerna förblir desamma, men innehållet i parentesen är avgörande för kameraanimationen.
Ange en "Starting Frame" som noll och lägg sedan in dina formler i parentesen. Det är viktigt att förstå betydelsen av de formler du matar in här. Dessa formler beskriver kamerans position över tid.
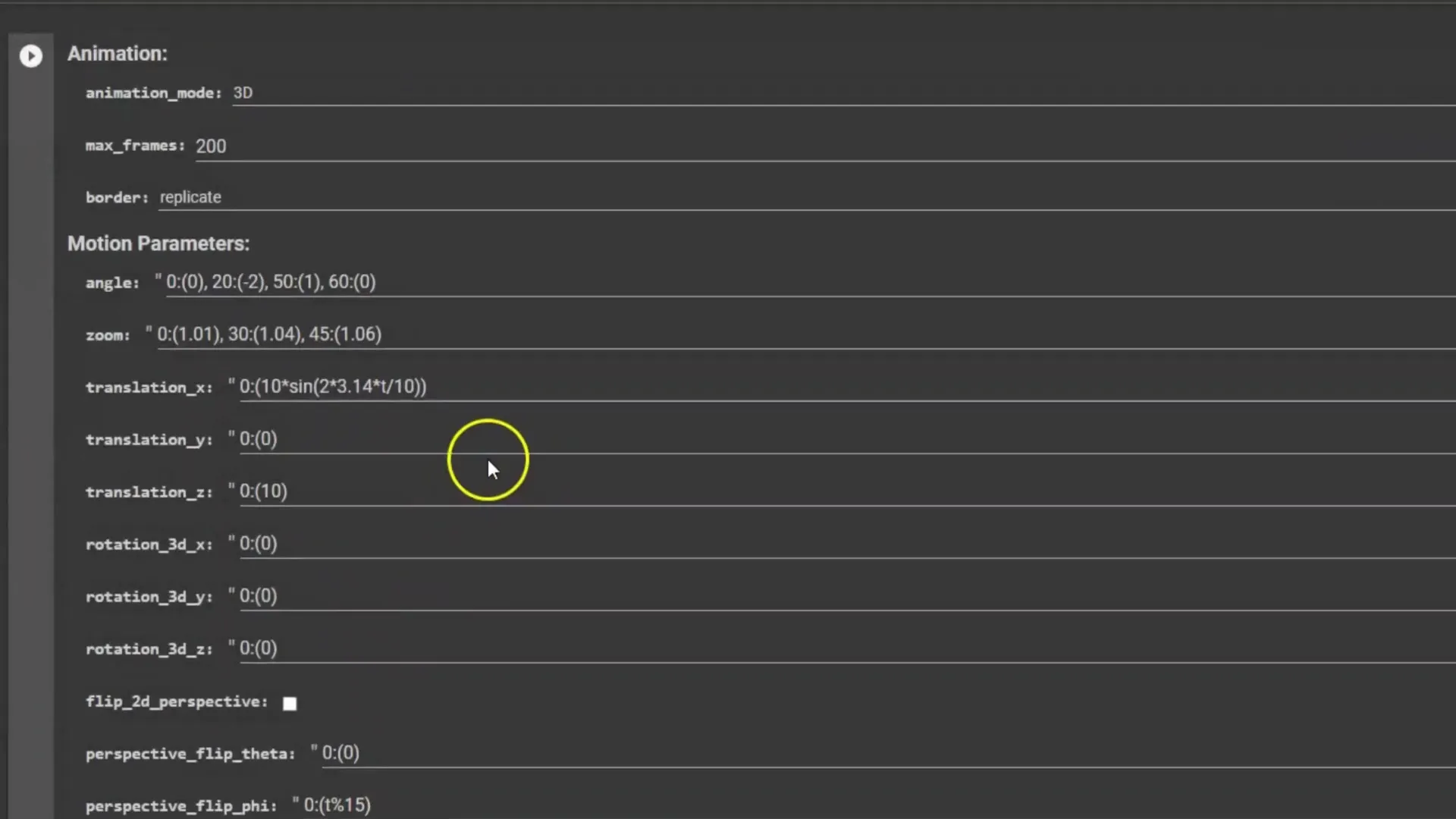
Till exempel, när jag går in i en plattform som ChatGPT, kan jag ställa enkla frågor om kameraaxlar för att få förståelse för hur det fungerar. Svaret att kamerarörelser beskrivs över tid är mycket användbart.
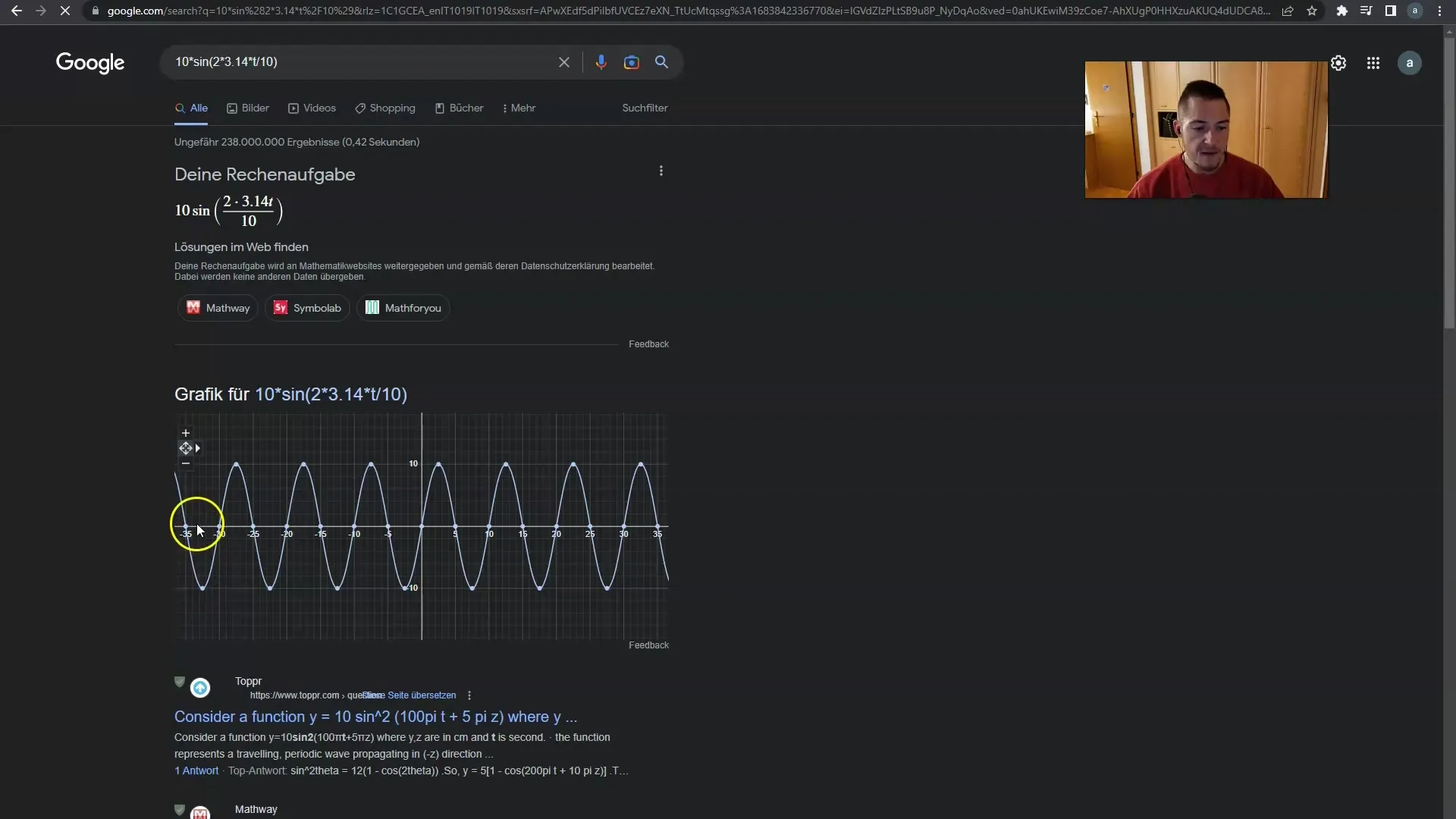
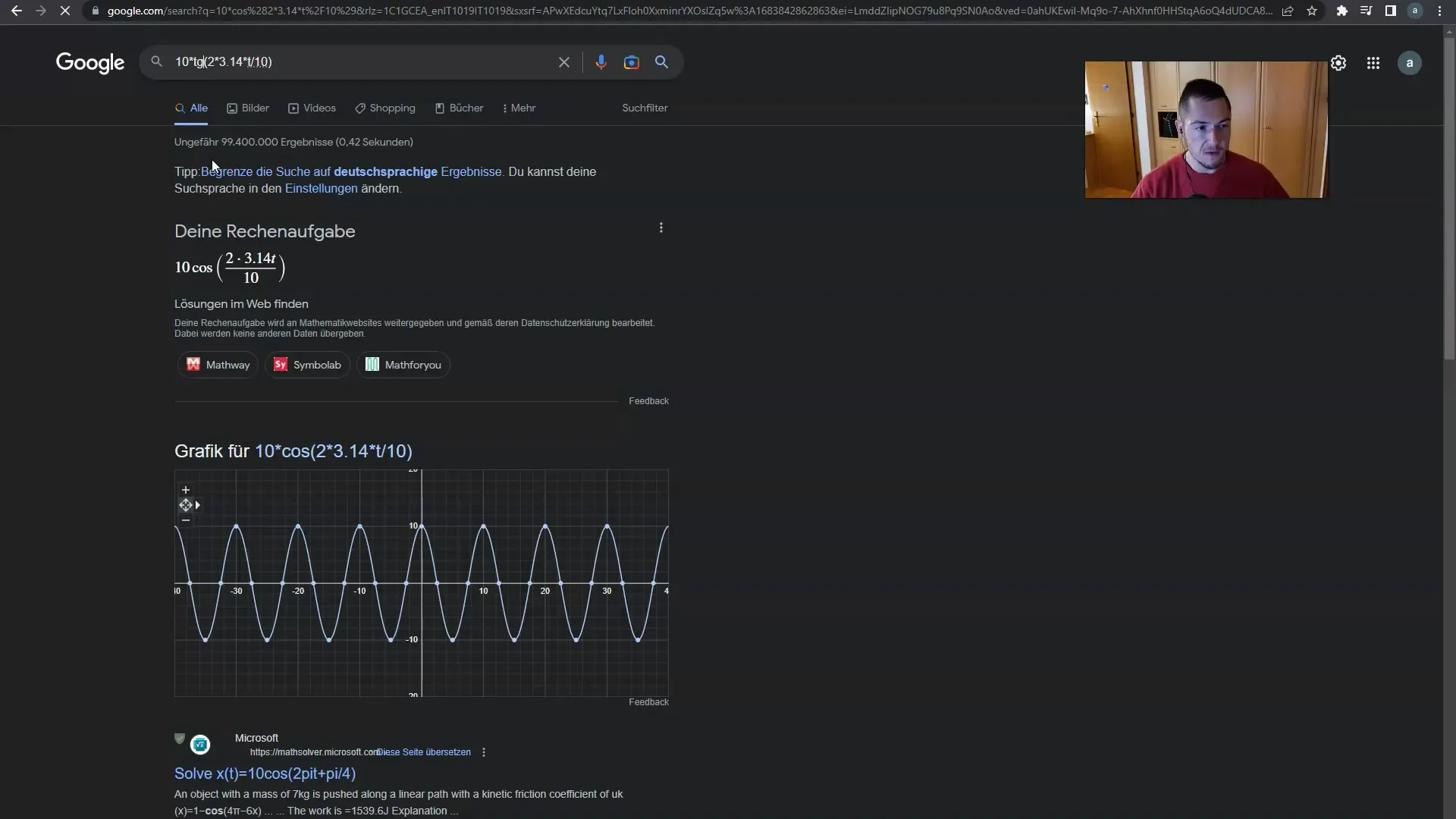
Jag har också sökt en grafisk representation för att bättre förstå hur kameran fungerar. Genom Google hittade jag en grafik som tydligt visar kamerans rörelser. Du ser att kameran rör sig upp och ner, och allt detta sker enligt beräkningarna i parentesen.
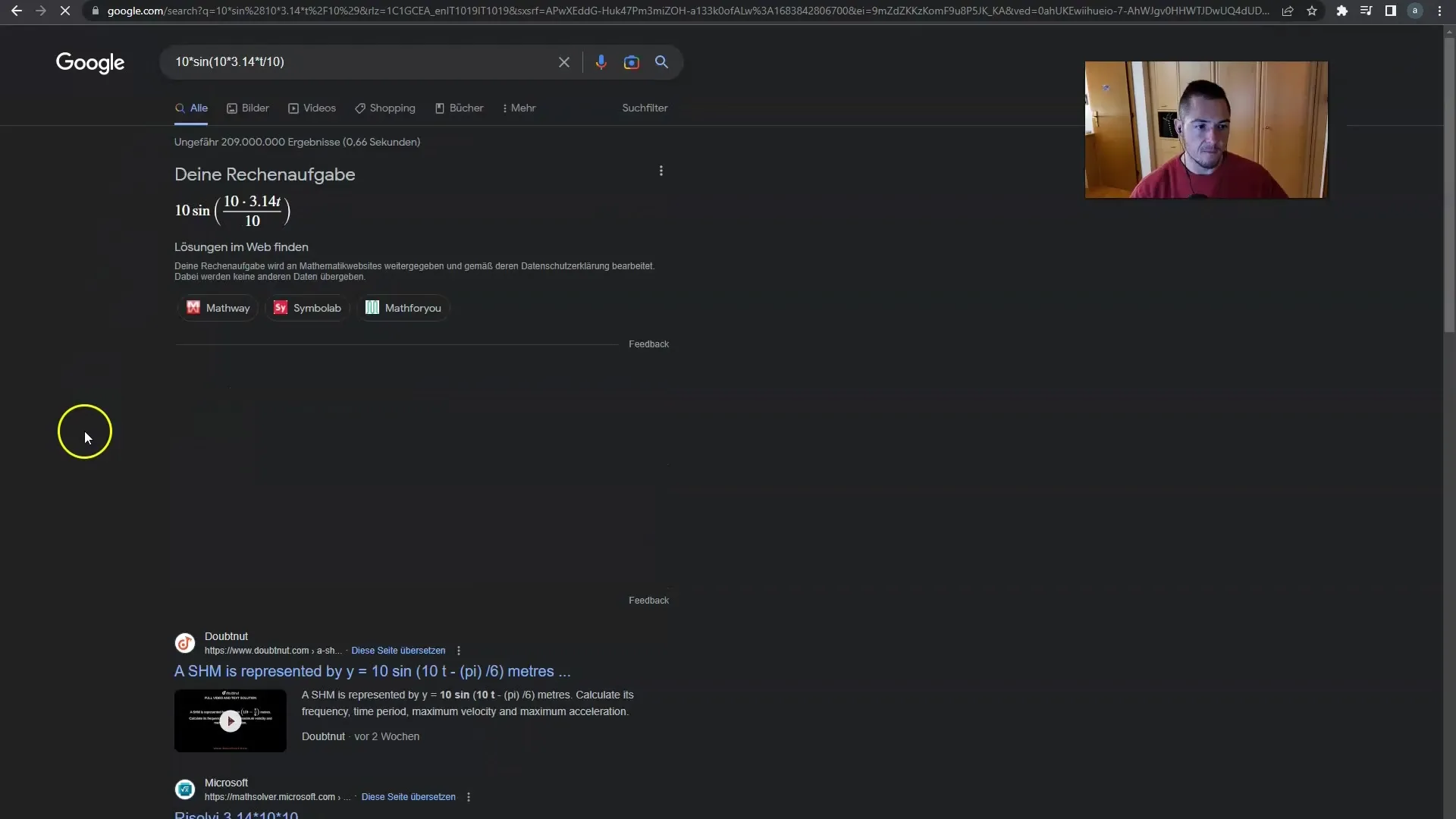
En mycket intressant insikt är att du också kan anpassa formlerna efter dina önskemål. Du kan till exempel ersätta sinuskurvan med cosinus och se hur kamerans beteende förändras.
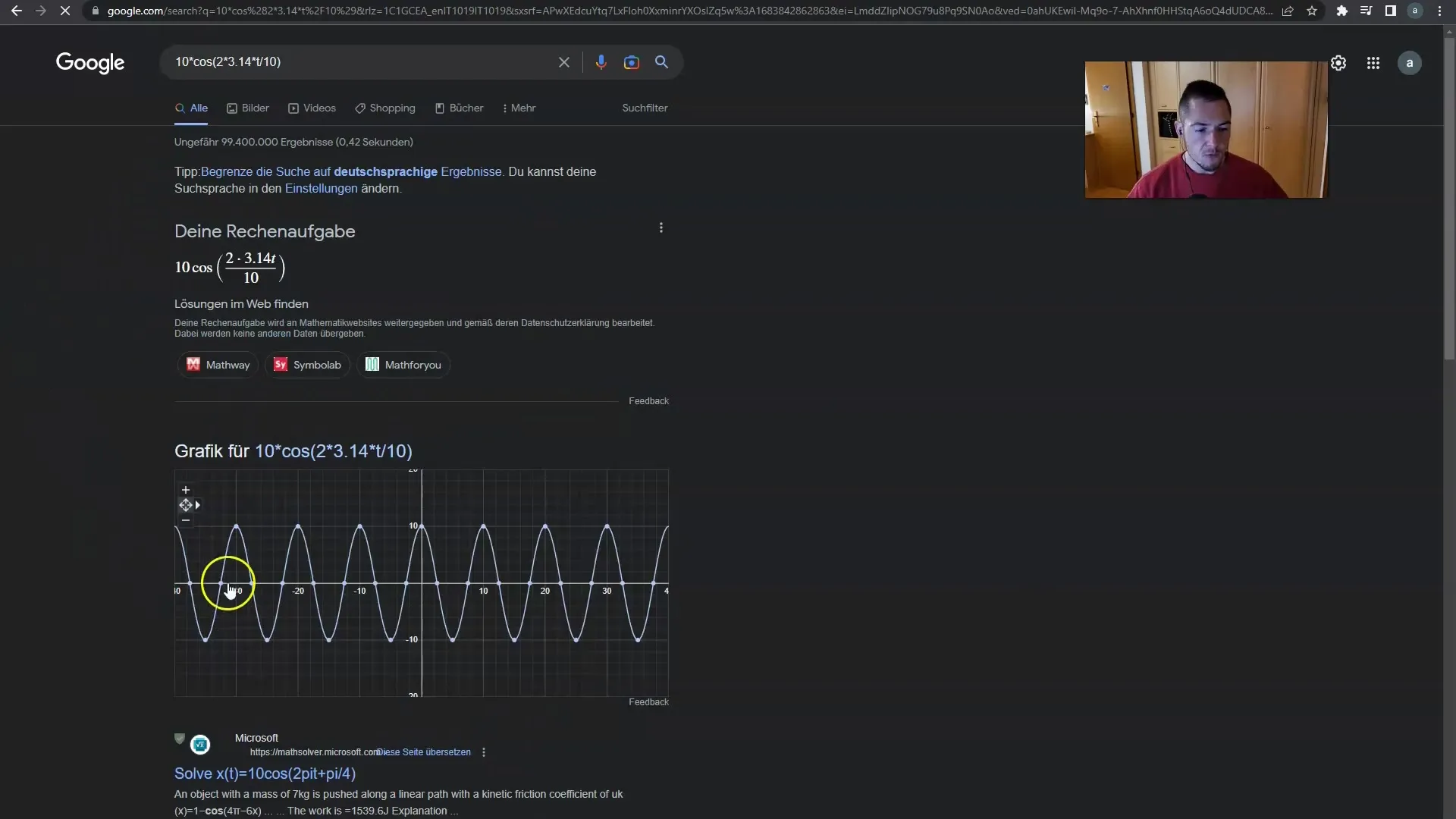
Vad som händer i parentesen påverkar hur högt och lågt kameran svänger eller skakar. Detta är grunden för rörelserna på tidslinjen som du kan skapa.
Om du vill prova något annorlunda kan du också använda tangens för att bli ännu mer kreativ i kameraanimationen.
Om något inte fungerar som du vill är det inte hela världen. Du kan justera värdena i parentesen och experimentera. Om du lägger till eller ändrar funktionen flera gånger ser du snabbt hur kameran beter sig.
Om du vill kan du förstärka effekten genom att multiplicera värden. Det är perfekt för att göra animationen mer spännande och intressant.
Det går att ändra formlerna från och med frame 25 och därmed införa en helt ny kamerarörelse. Om du inför nya rörelser från och med detta frame, hjälper det dig att göra animationen mer dynamisk.
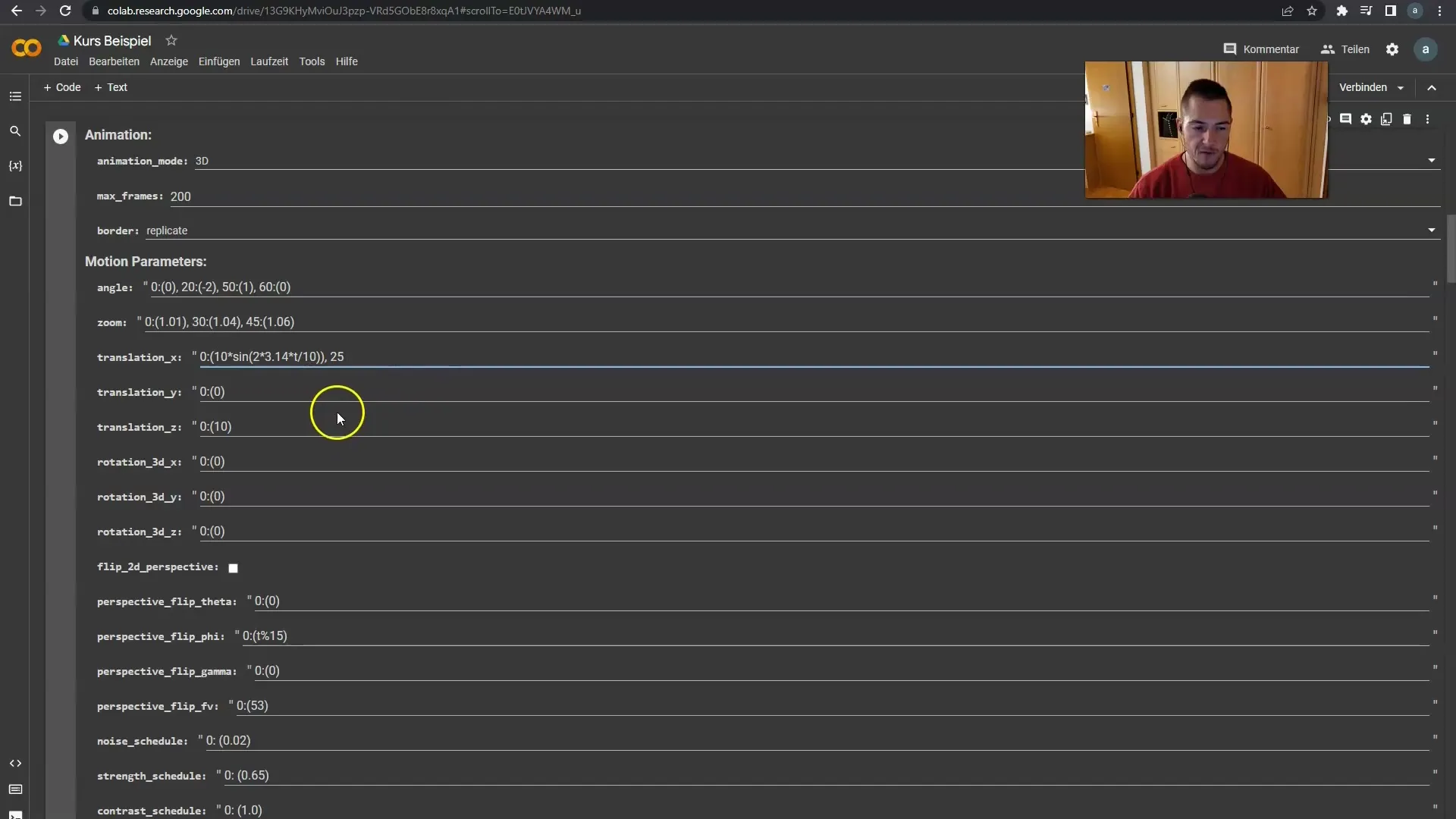
Det är viktigt att du kan anpassa formlerna för att skapa olika rörelser.
Om du vill arbeta i 3D blir det lite mer komplicerat eftersom du också måste beakta z-axeln. Se till att justera 3DX, 3DY och 3DZ enligt behov, eller låt dem vara noll om du inte vill ha någon effekt.
Sammanfattningsvis kan du flytta, rotera eller skapa 3D-animationer för alla objekt i ditt projekt. Du har kontrollen för att kreativt arbeta med dessa formler.
En viktig anmärkning: Du måste experimentera med formlerna och se vilka variationer som ger bäst resultat.
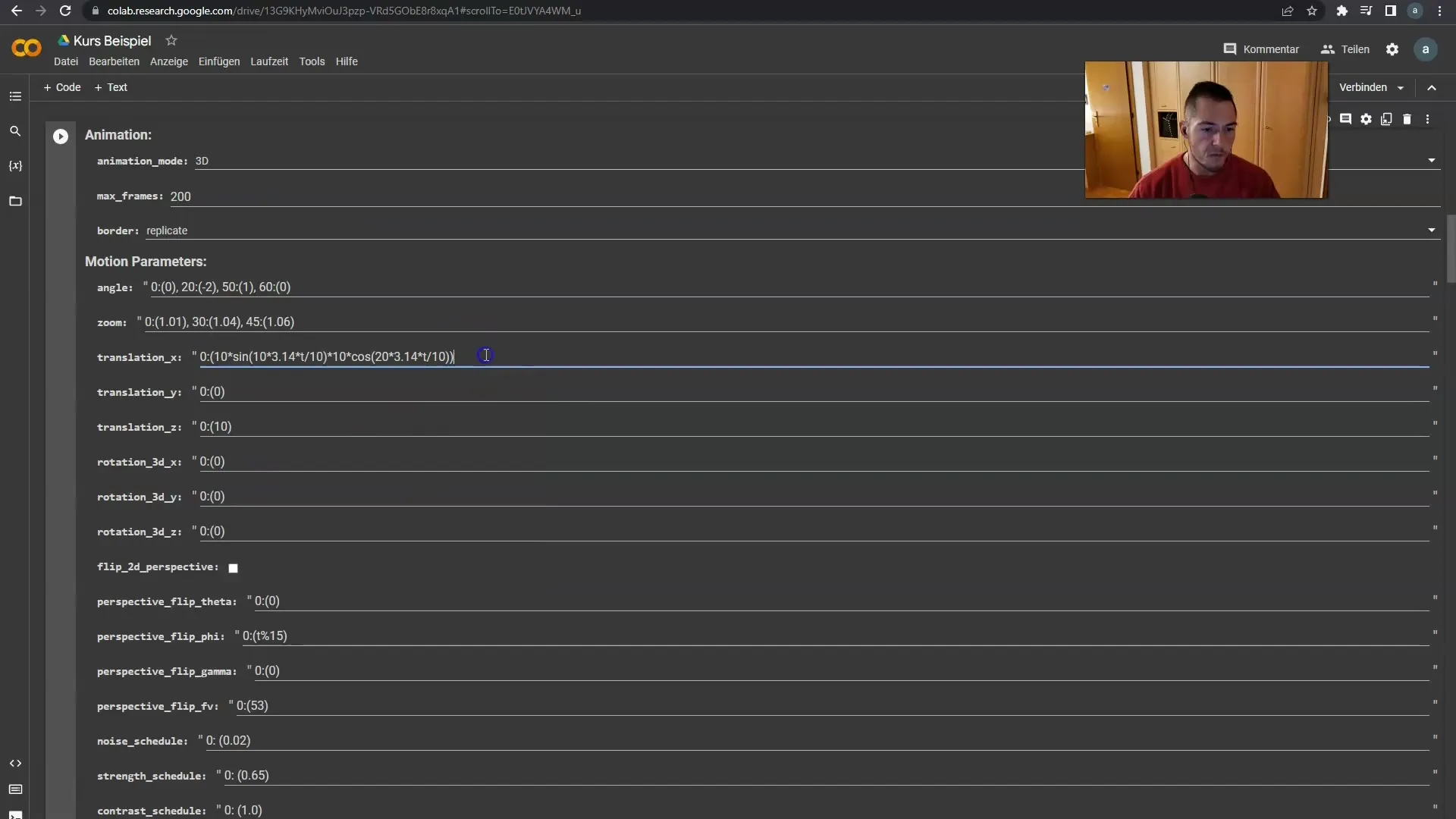
När du väl har förstått de grundläggande principerna och hanteringen av formlerna kommer det att vara mycket lätt för dig att uppnå kreativa resultat.
Sammanfattning
I den här handledningen har du lärt dig hur du implementerar formler i Deforum Stable Diffusion för att styra kamerans rörelser. Du har fått insikt i vikten av olika funktioner och lärt dig att ofullkomliga inmatningar inte omedelbart har negativa effekter. Experimentera med olika värden och funktioner för att optimera och kreativt utforma dina animationer.
Vanliga frågor
Vilka är de viktigaste formlerna för kameraxlarna?Sinus, cosinus och tangens är de viktigaste funktionerna för att styra kamerarörelser.
Kan jag ändra formulerna utan att påverka animationen?Ja, du kan ändra värden i formulerna och se vilken effekt det har på animationen.
Hur kan jag göra kamerarörelserna mer dynamiska?Genom att anpassa eller multiplicera formulerna kan du göra rörelserna mer intressanta.
Måste jag använda z-axeln när jag jobbar i 3D?Ja, i 3D-applikationer är det nödvändigt att ta hänsyn till z-axeln medan x- och y-axlarna räcker för 2D.
Kan jag ändra formulerna i efterhand?Ja, du kan när som helst anpassa formulerna för att uppnå olika resultat.


