Chi-kvadrat-anpassningstest är en enkel metod för att testa hypotesen om en given dataserie följer en normalfördelning. I den här handledningen kommer du att lära dig hur du kan utföra Chi-kvadrat-testet i Excel för att avgöra om smartphoners försäljning följer en normalfördelning. Vi kommer att gå igenom processen steg för steg, från att skapa en klassificerad frekvenstabell till att beräkna teststorleken och jämföra den med det kritiska chi-kvadratvärdet.
Viktigaste insikter
- Chi-kvadrat-anpassningstestet hjälper till att testa normalfördelningar.
- Det är viktigt att skapa en klassificerad frekvenstabell.
- Teststorleken jämförs med ett kritiskt värde för att antingen förkasta eller acceptera nollhypotesen.
Steg-för-steg-guide
Steg 1: Förbered data
För att utföra Chi-kvadrat-testet behöver du först data. Kopiera smartphoners försäljning till ett Excel-ark. Se till att dina data är organiserade i en enda kolumn.

Steg 2: Skapa histogram
För att få en första visuell indikation på fördelningen, skapa ett histogram av dina data. Gå till "Infoga" och välj "Diagram". Lägg till ett histogram genom att välja området för datan.
Steg 3: Skapa klassificerad frekvenstabell
För Chi-kvadrat-testet behöver du en klassificerad frekvenstabell. Räkna först ut antalet klasser för din tabell - i det här fallet använder vi sex klasser. Beräkna intervallbredden och skapa tabellen därefter.
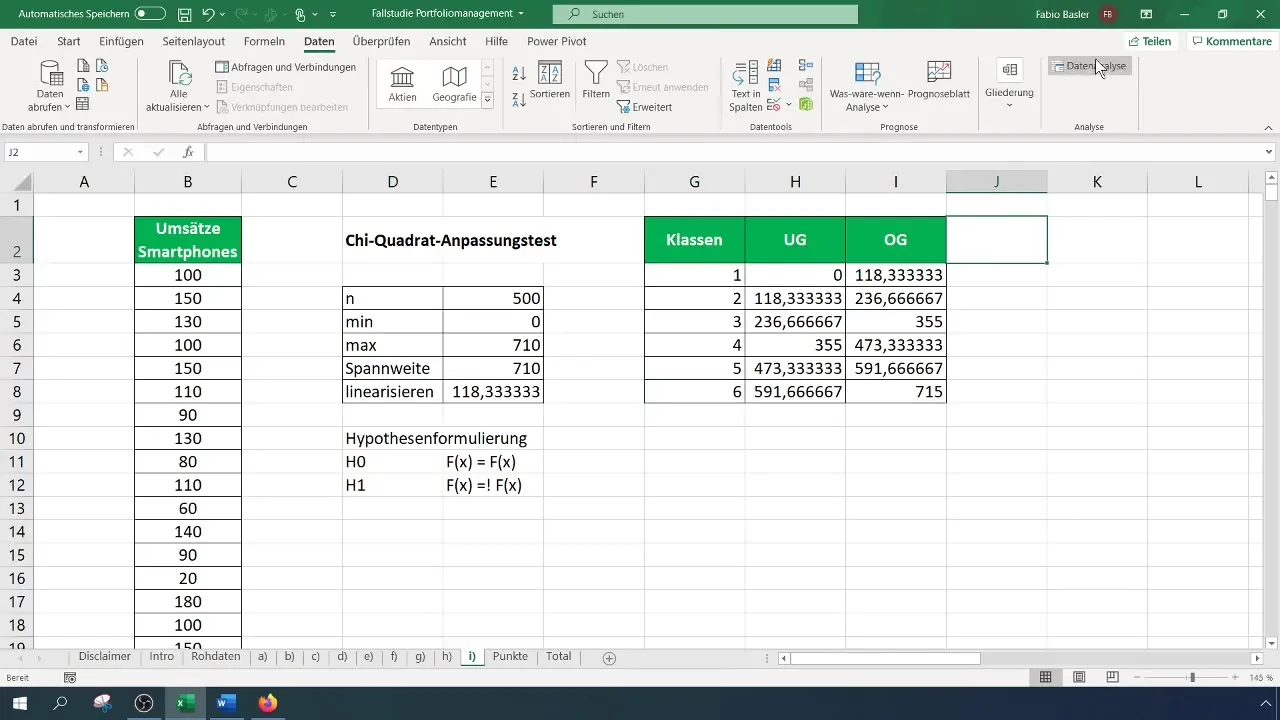
Steg 4: Beräkna frekvenser
Nu måste du beräkna de observerade frekvenserna för varje klass. Gå till "Dataanalys" i menyn och välj "Histogram". Välj inmatningsområdet för dina data och klassgränserna. Ange utdataområdet för frekvenstabellen.
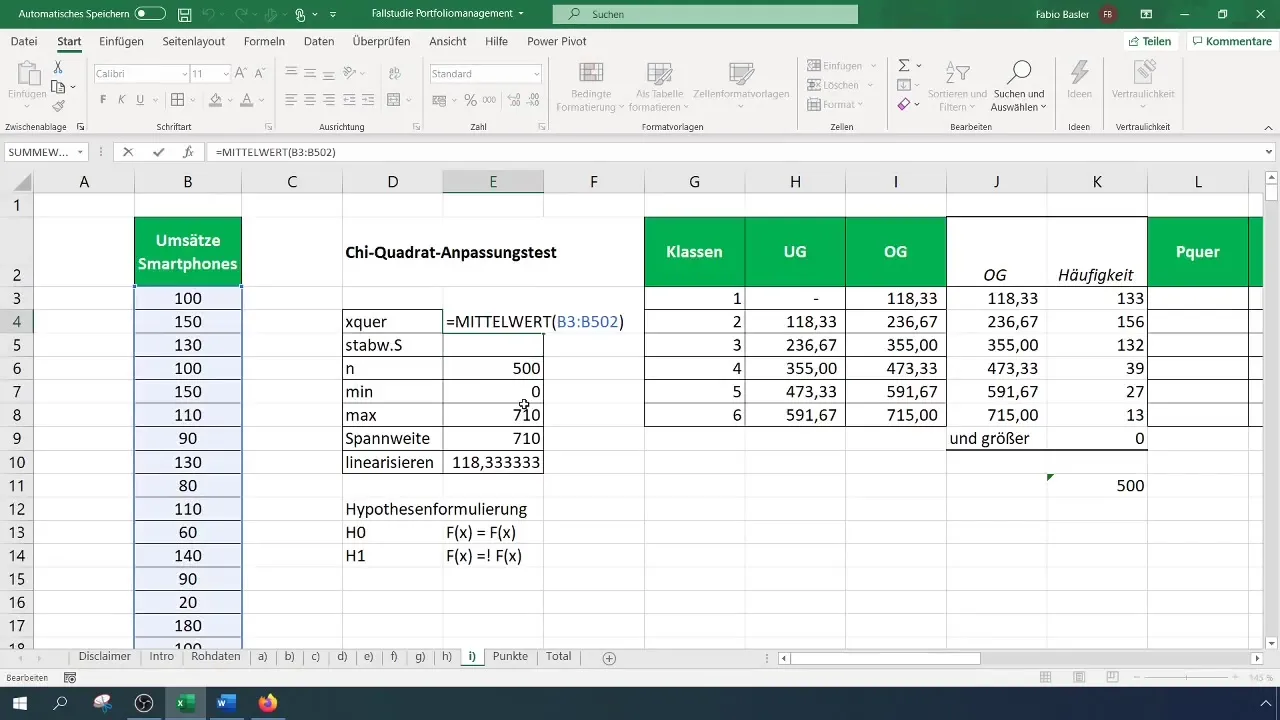
Steg 5: Beräkna förväntade frekvenser
För att beräkna de förväntade frekvenserna, beräkna sannolikheten för varje klass baserat på antagandet om normalfördelning. Du behöver medelvärdet och standardavvikelsen för dina data för detta ändamål.
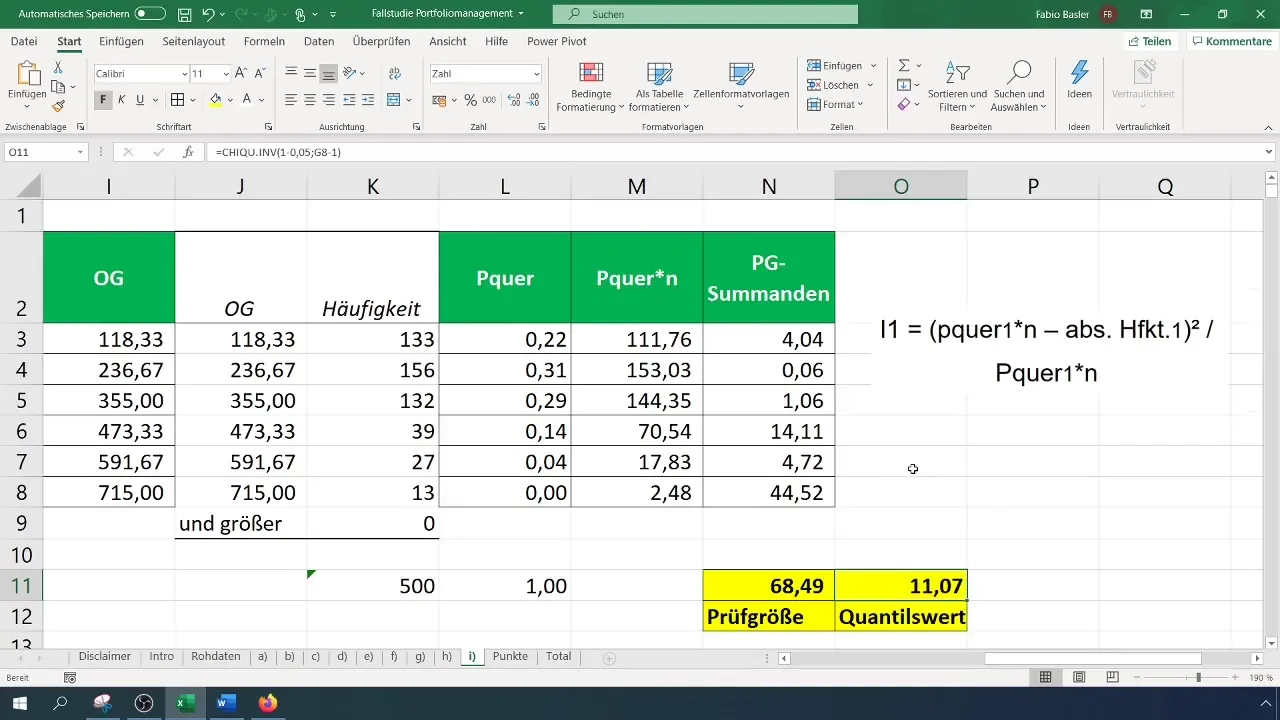
Steg 6: Beräkna teststorlek
Beräkna teststorleken (Chi-kvadrat) med formeln:
[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} ]
där (O_i) är de observerade och (E_i) är de förväntade frekvenserna. Du kan utföra denna beräkning i Excel genom att spara de olika komponenterna i separata celler.
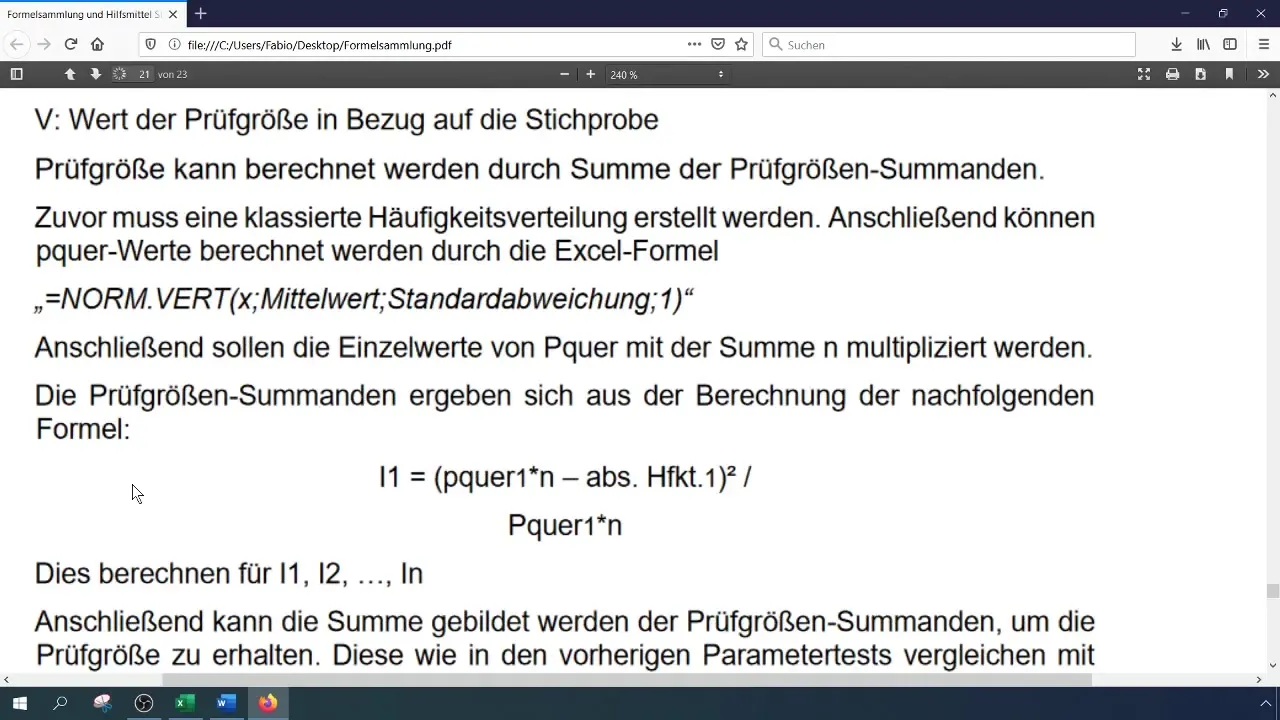
Steg 7: Beräkna kritiskt värde
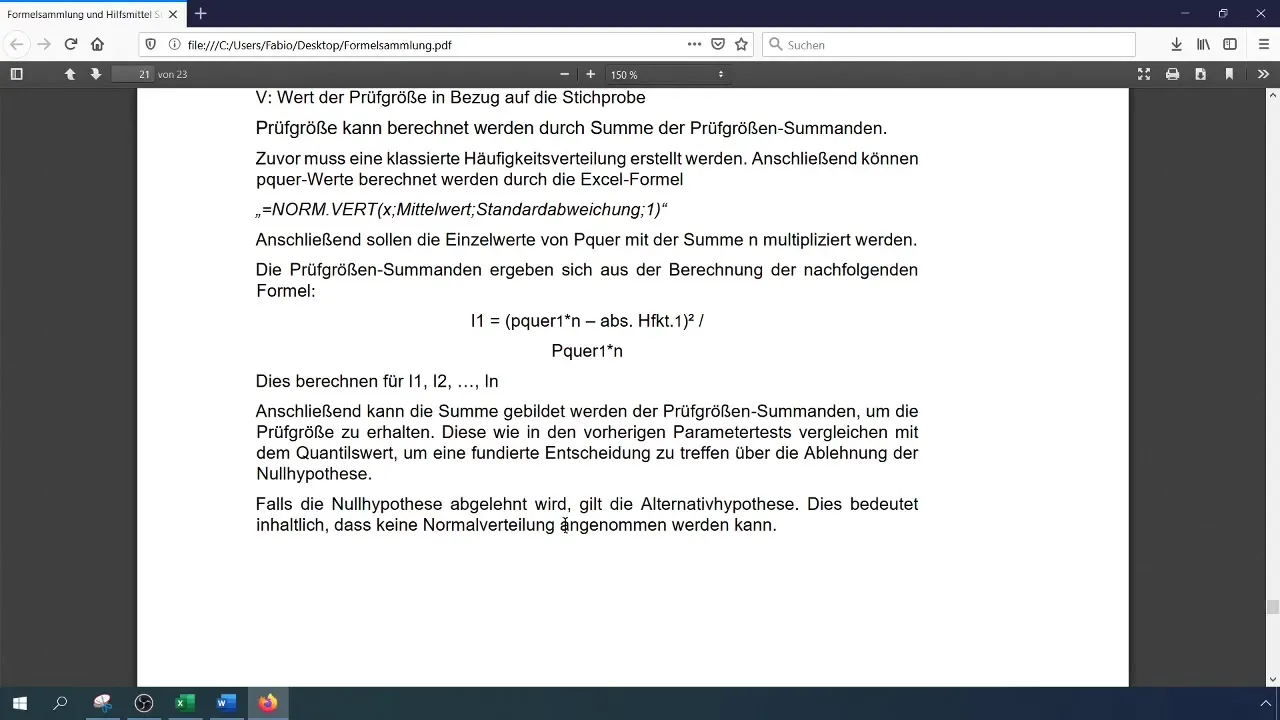
För att utvärdera teststorleken måste du beräkna det kritiska värdet ( \chi^2 ) för ditt konfidensintervall och antalet frihetsgrader. Antalet frihetsgrader för Chi-kvadrat-testet är (k - 1), där (k) är antalet klasser.
Steg 8: Testa hypoteser
Jämför din beräknade teststorlek med det kritiska värdet. Om teststorleken är större än det kritiska värdet förkastas nollhypotesen, vilket innebär att datan inte är normalfördelad. Annars accepterar du nollhypotesen.
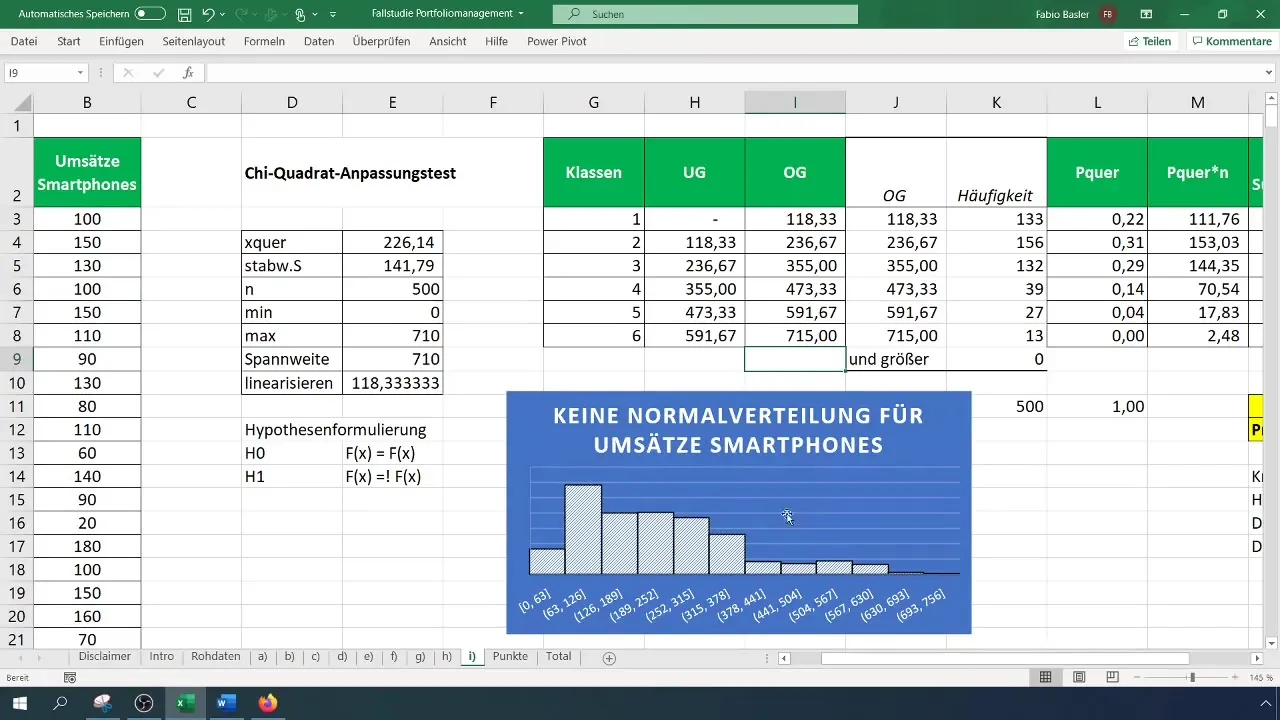
Steg 9: Sammanfatta resultat
Behåll dina resultat och utvidga dem med grafiska data och hypotesprov. Glöm inte att kontrollera ditt histogram för visuell bekräftelse att fördelningen inte är normal.
Sammanfattning
Under denna handledning har du lärt dig hur du utför Chi-quadranpassningstestet i Excel för att analysera normalfördelningen av din smartphone-försäljning. Stegen innefattar att skapa en frekvenstabell, beräkna förväntade frekvenser, teststorleken och slutligen jämföra dessa med det kritiska värdet.
Vanliga frågor
Vad är Chi-quadranpassningstestet?Chi-quadranpassningstestet testar om den observerade frekvensfördelningen motsvarar en normalfördelning.
Hur många klasser behöver jag för frekvenstabellen?Vanligtvis är det meningsfullt att ha minst 5 till 10 klasser för att analysera data på ett meningsfullt sätt.
Vad gör jag om nollhypotesen avvisas?Om du avvisar nollhypotesen innebär det att datan inte är normalfördelad.
Hur beräknar jag det kritiska Chi-quadra-värdet?Det kritiska värdet läses av i en Chi-quadra-tabell med hänsyn till frihetsgraderna och den önskade signifikansnivån.


