Det är avgörande att fatta välgrundade beslut inom affärs- och försäljningsområdet baserat på dataanalys. Ett tvisidigt konfidensintervall möjliggör att du kan bestämma området där det sanna genomsnittsvärdet av en parameter med en viss sannolikhet finns. I denna handledning visar jag dig hur du med hjälp av Excel kan beräkna området för intervallgränserna för veckoförsäljningen för ett försäljningsteam med en förtroendesannolikhet på 93 %.
Viktigaste insikter
Några av de väsentliga aspekterna av det tvisidiga konfidensintervallet inkluderar:
- Beräkning av medelvärdet som ett uppskattat värde för parametern.
- Bestämning av standardavvikelsen från urvalet.
- Tillämpning av formler för att fastställa nedre och övre gränser för intervallet.
- Att ta hänsyn till förtroendesannolikheten för att positionera intervallet.
Steg-för-steg-guide
Först behöver vi en solid förståelse för begreppen och stegen som sammanfattar denna process.
Steg 1: Förberedelse av data
Först bör du förbereda data för försäljningsteam A. Filtrera de relevanta data och kopiera dem till ditt Excel-dokument.
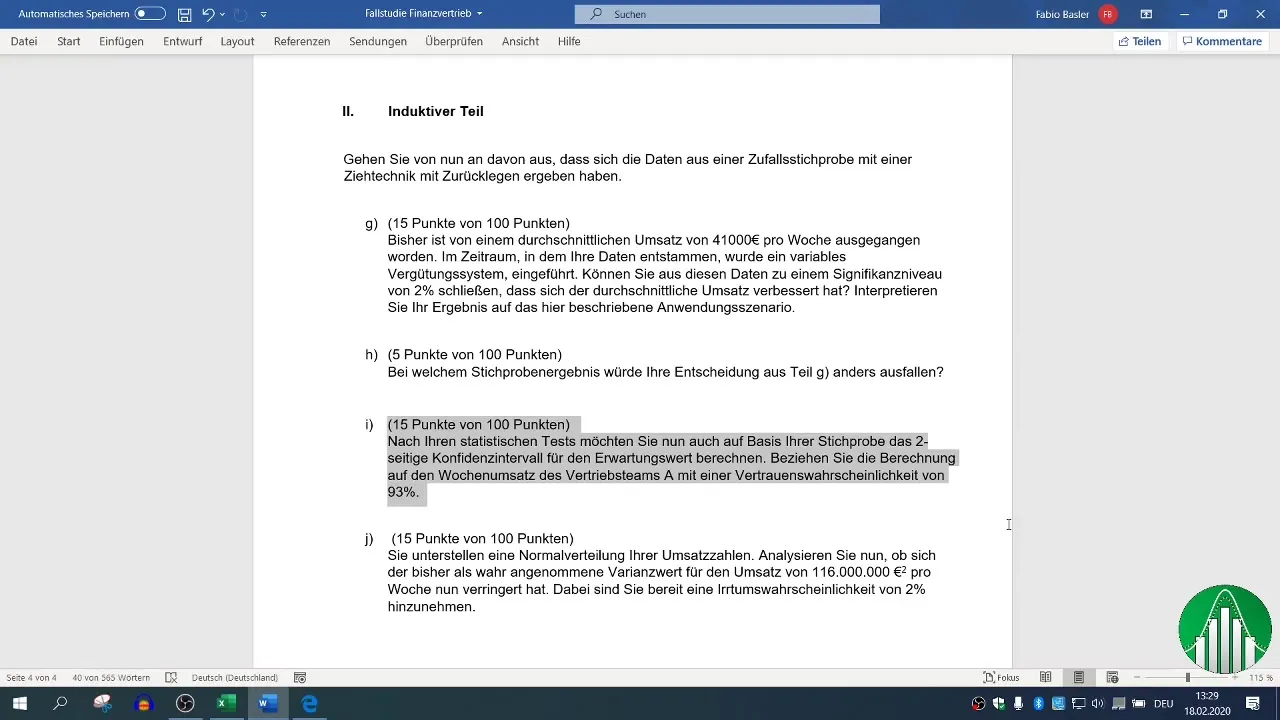
Steg 2: Beräkning av medelvärdet
För att beräkna konfidensintervallet är det första steget att bestämma medelvärdet, som fungerar som en uppskattning av förväntad försäljning. I Excel kan du göra detta med formeln =MEDELVÄRDE(Område), där "Område" är cellerna som innehåller data för veckoförsäljningen för försäljningsteam A.
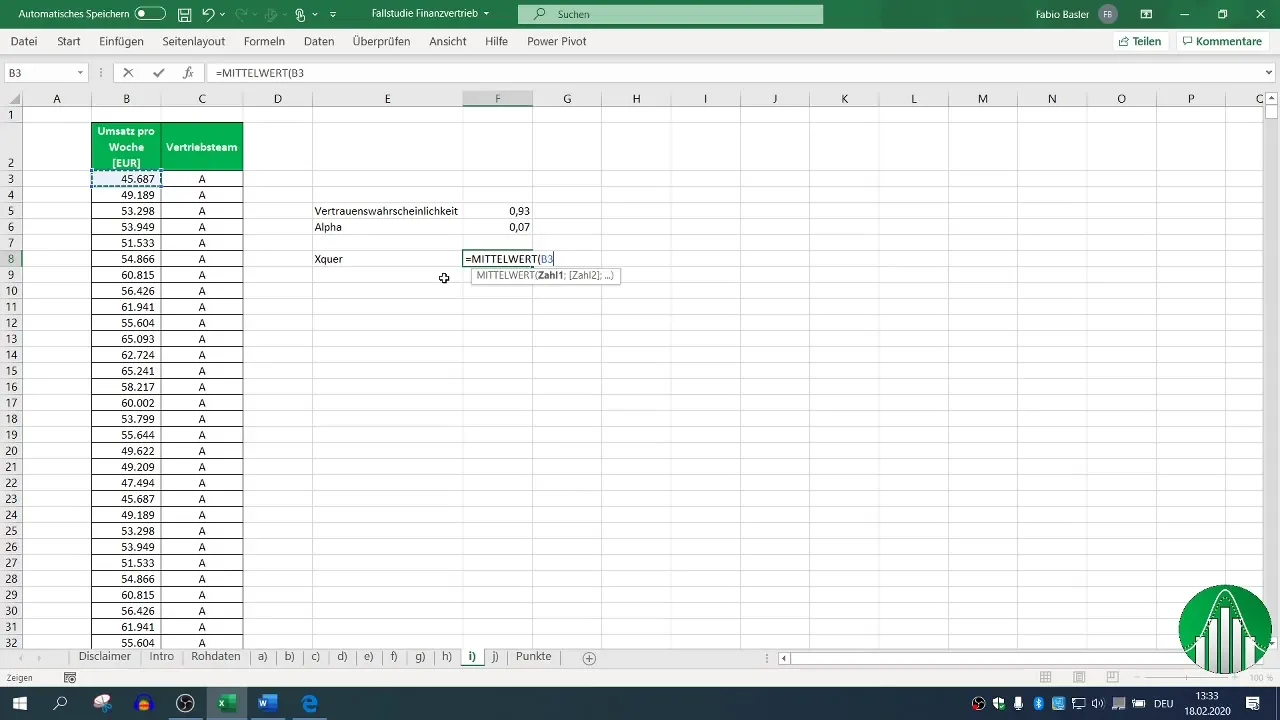
Steg 3: Beräkning av standardavvikelsen
Standardavvikelsen (σ) är viktig för beräkningen av det tvisidiga konfidensintervallet. Du kan beräkna den i Excel med formeln =STDEV.S(Område). Se till att välja rätt formel för standardavvikelsen från urvalet.
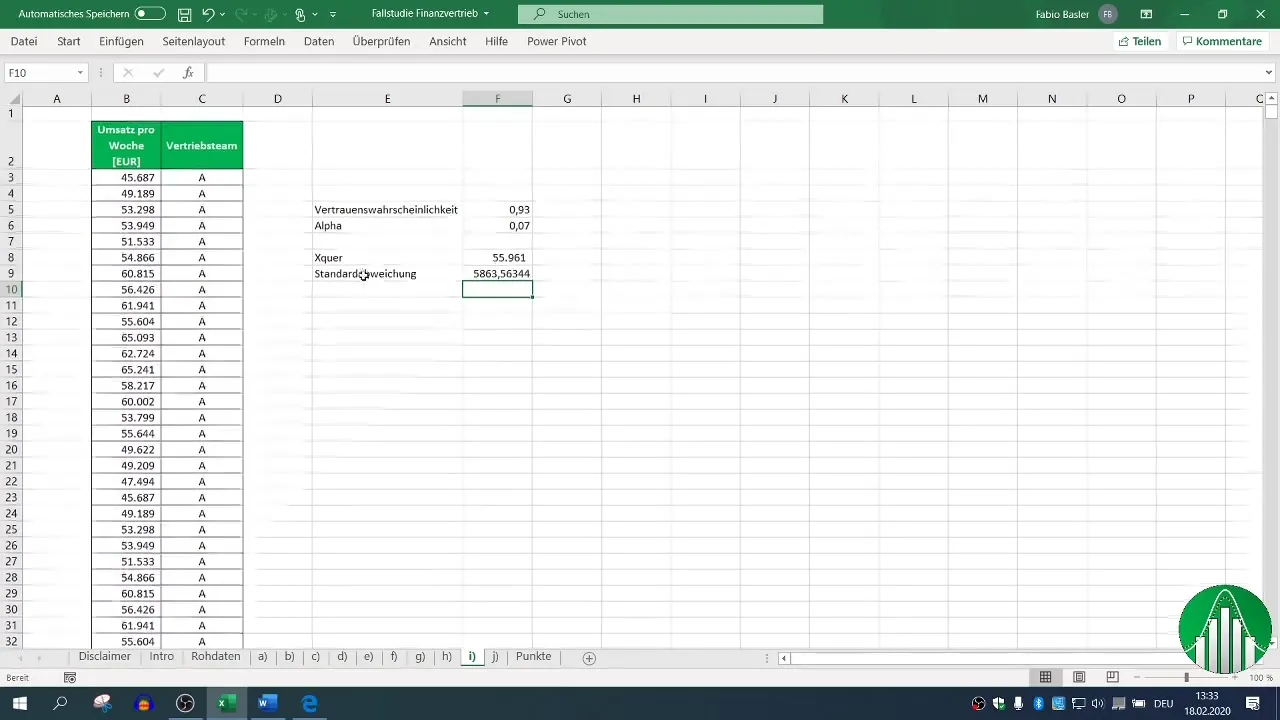
Steg 4: Bestämning av urvalstorlek
Därefter behöver du bestämma urvalstorleken (n). Lägg till antalet poster du har samlat för försäljningsteam A. I detta exempel utgår vi från 33 poster.
Steg 5: Beräkning av medelvärdets standardavvikelse (σ_m)
För att beräkna konfidensintervallet är det nödvändigt att beräkna medelvärdets standardavvikelse, vilket enkelt är standardavvikelsen dividerat med kvadratroten av urvalstorleken.
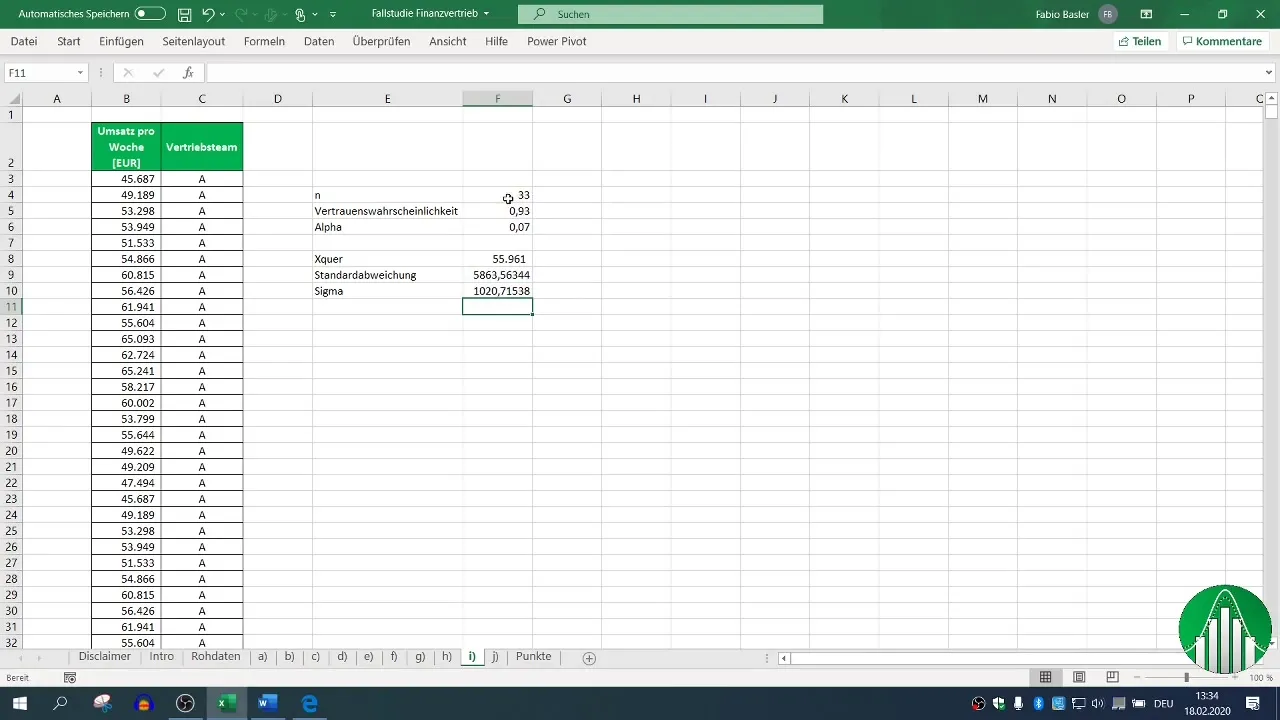
Steg 6: Bestämning av kvantil
För att beräkna det tvisidiga konfidensintervallet behöver du kvantilen. Eftersom du anger en förtroendesannolikhet på 93 % är α 7 % och fördelningen av kvantilen hittar du genom att använda Excel-funktionen.
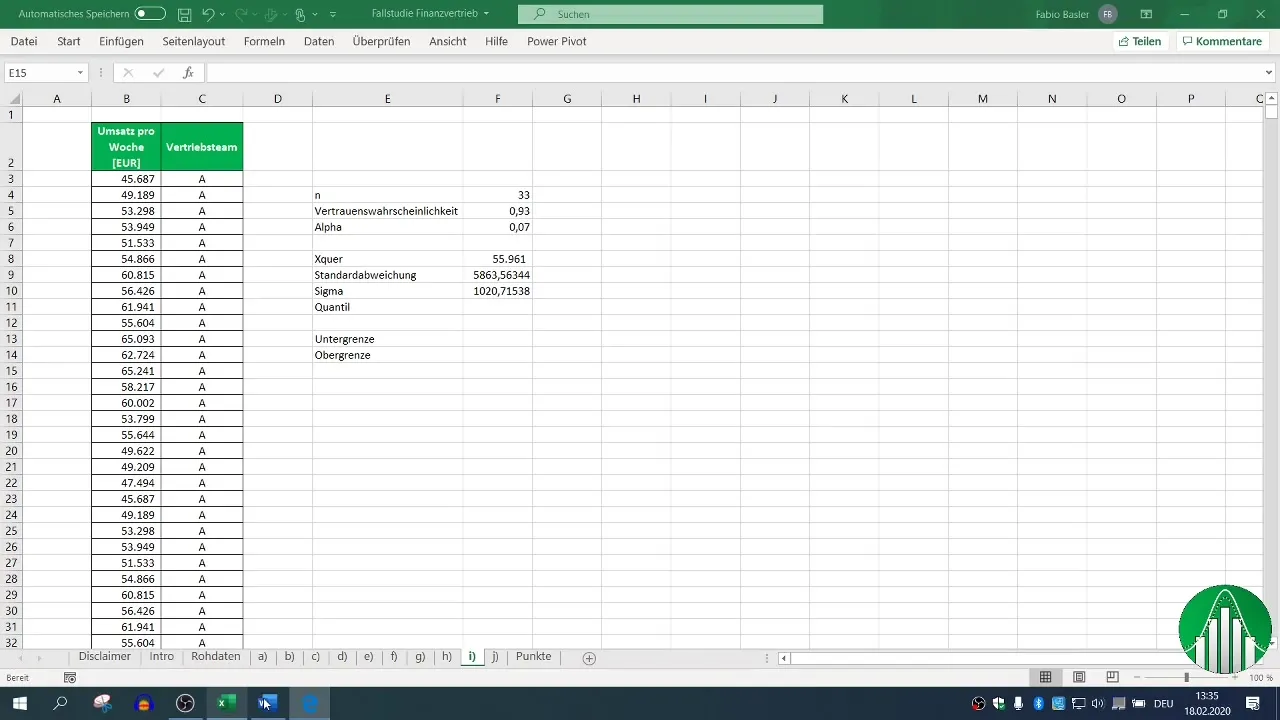
Steg 7: Beräkning av nedre gränsen
Nu beräknar vi den nedre gränsen för konfidensintervallet. För detta drar du bort produkten av kvantilen och standardavvikelsen av medelvärdet (x̄) från medelvärdet.
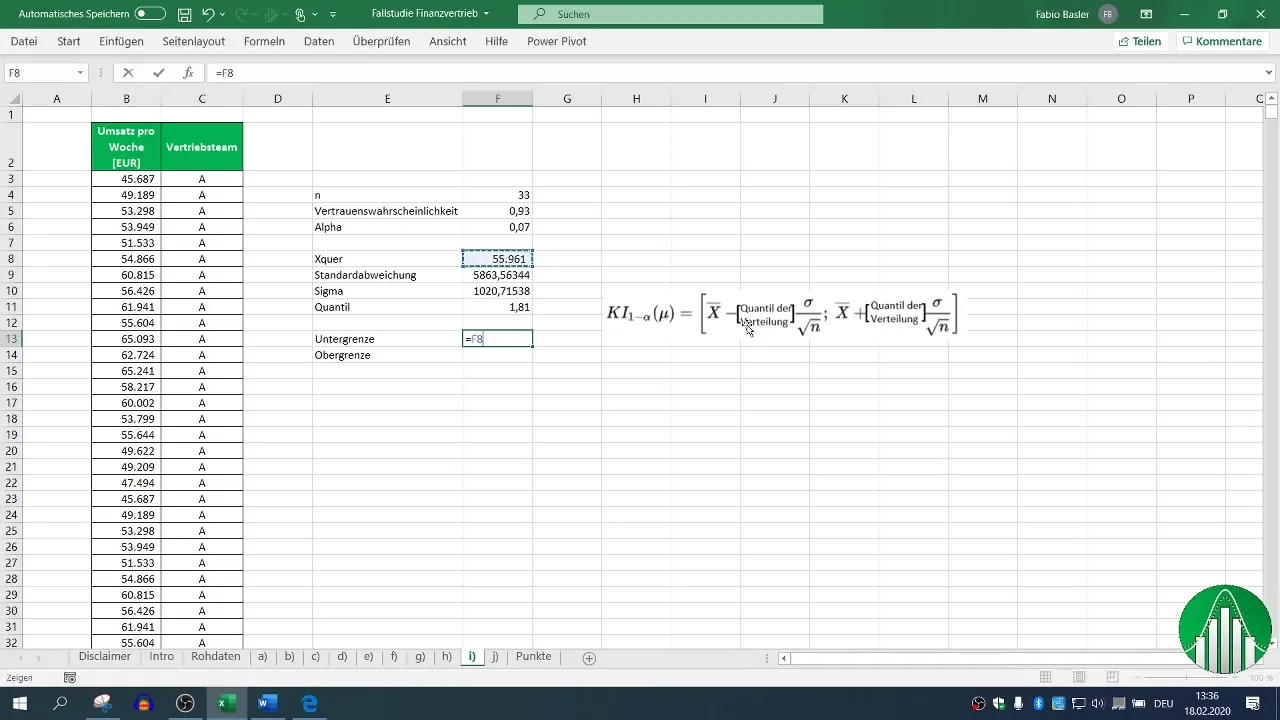
Steg 8: Beräkning av övre gränsen
Den övre gränsen beräknas på liknande sätt, men du lägger till produkten istället för att subtrahera.
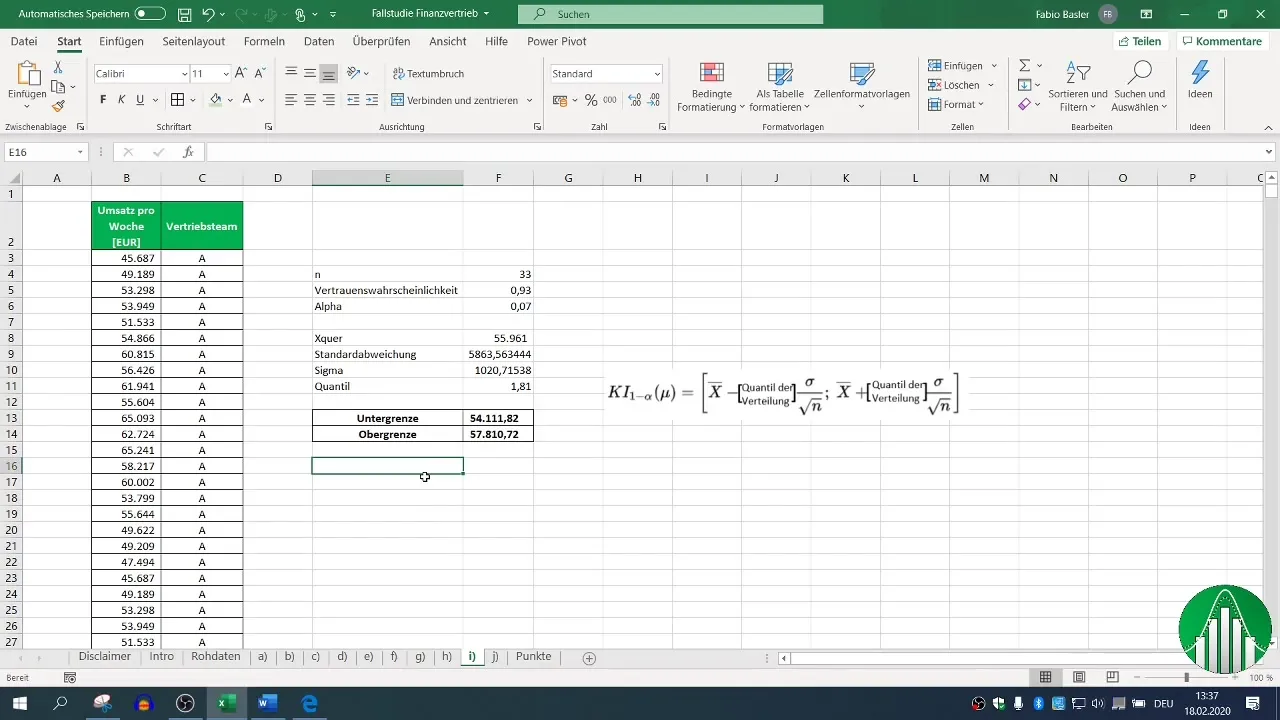
Steg 9: Tolka resultatet
Efter dessa beräkningar får du det tvisidiga konfidensintervallet för veckoförsäljningen för försäljningsteam A. I vårt exempel ligger intervallet mellan 54,111 och 57,810. Det innebär att det sanna genomsnittliga försäljningsvärdet ligger inom detta område med en förtroendesannolikhet på 93 %.
Sammanfattning
Genom att exakt beräkna det tvisidiga konfidensintervallet kan du göra precisa bedömningar av framtida försäljning. Du har lärt dig hur du kan förbereda relevanta data, beräkna medelvärdet och standardavvikelsen och slutligen fastställa intervallets gränser. Med denna metod kan du fatta datadrivna beslut inom ditt försäljningsområde.
Vanliga frågor
Vad är ett tvåsidigt konfidensintervall?Det är ett intervall som omfattar uppskattningen av en parameters värde med en viss sannolikhet.
Vad gör jag om jag inte har en normalfördelning?Om normalfördelningen inte finns kan du också använda en godtyckligt distributionsantagande.
Varför är kvantilen viktig?Kvantilen hjälper dig att bestämma avstånden för övre och undre gränserna av konfidensintervallet.


