Rangkorrelationsanalysen är av central betydelse vid statistisk undersökning av relationer mellan variabler. Speciellt när det kommer till ordinalskalade data, är Spearman-rankningskorrelationen en värdefull metod för att upptäcka mönster och samband. I den här guiden kommer du steg för steg att lära dig hur du kan beräkna rangkorrelationen enligt Spearman för en enkät med hjälp av Excel.
Viktigaste insikter
- Rangkorrelation mäter styrkan och riktningen av ett monotont förhållande mellan två ordinala variabler.
- Spearman-rankningskorrelationskoefficienten är särskilt lämplig när en variabel är ordinal och den andra är metriskt skalerad.
- Beräkningen i Excel kan göras med hjälp av enkla formler och funktioner.
Steg-för-steg guide
Först definierar vi de variabler som vi vill analysera. I det här fallet handlar det om kundernas nöjdhet (ordinalt skalerad, värden 1-3) och antalet beställningar (metriskt skalad).
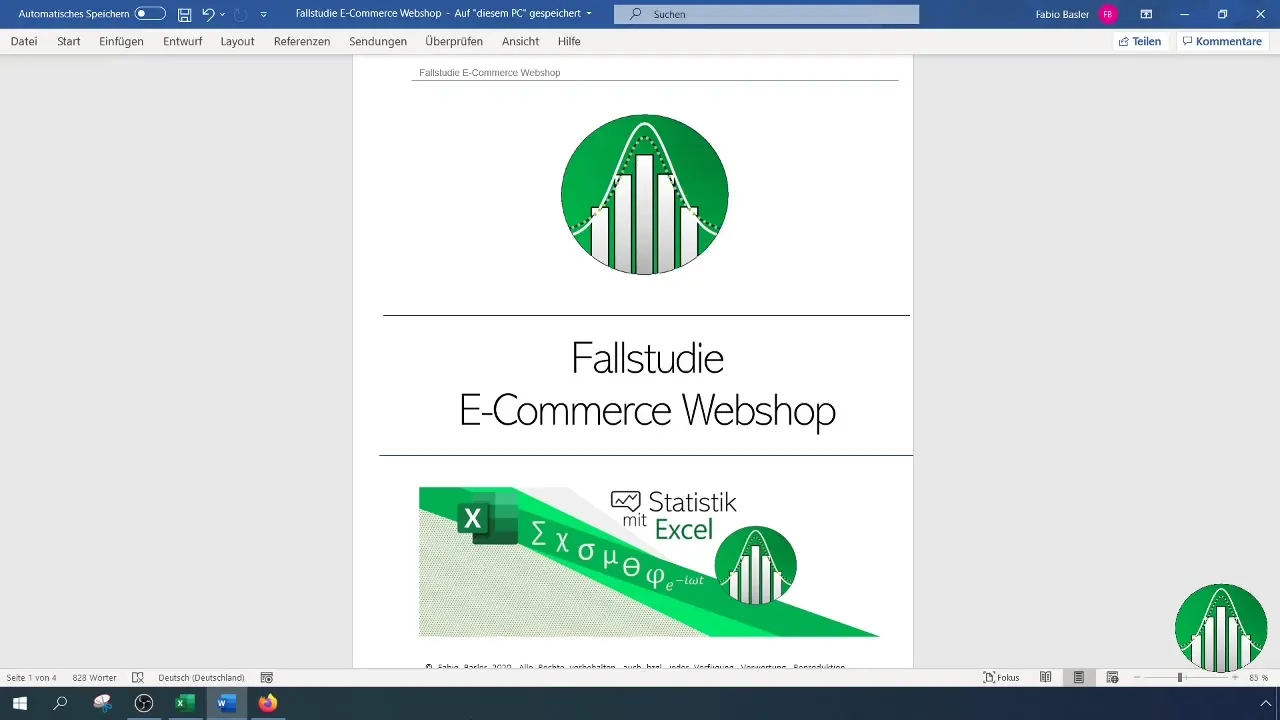
För att skapa en ranking för nöjdhet och antal beställningar behöver du en tabell som innehåller de motsvarande datan. Se till att du matar in dessa data i Excel.

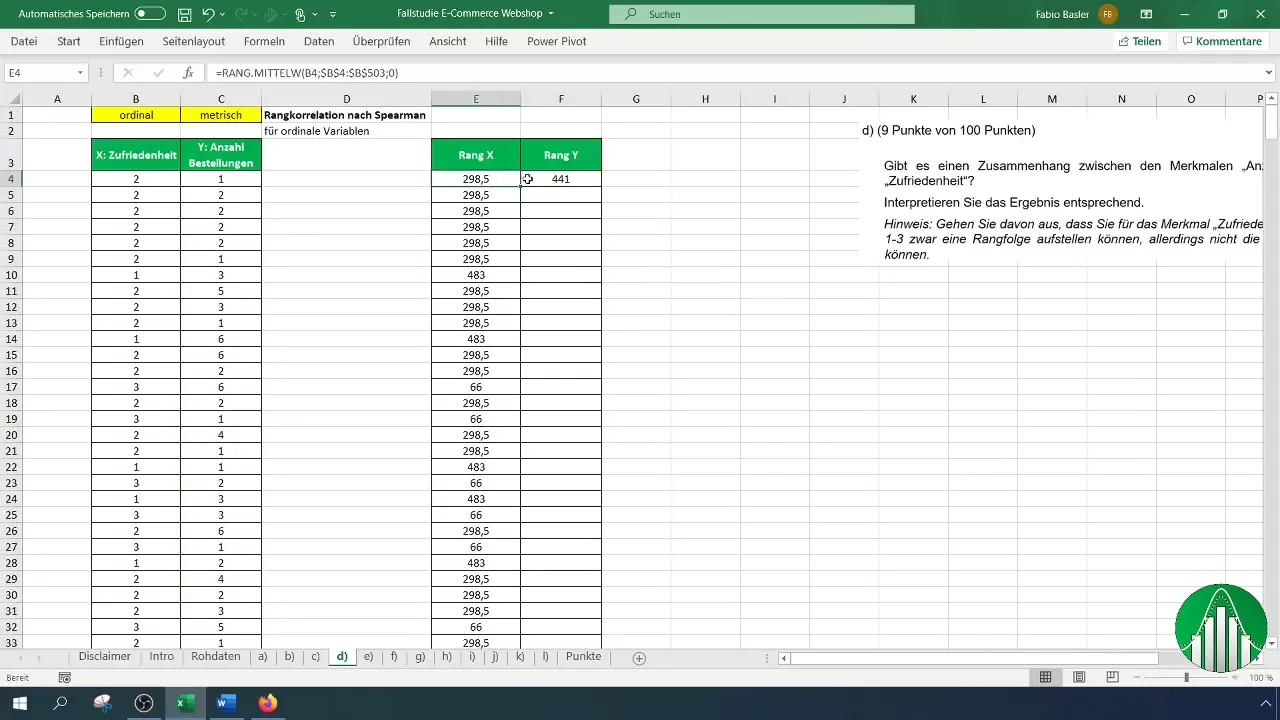
Efter att du har matat in dina data i Excel, tittar vi på beräkningen av rangkerrelationen enligt Spearman. För detta använder vi funktionen "Rang.Mittel" i Excel, som returnerar rangen för ett tal i en lista. För nöjdhet använder vi formeln:
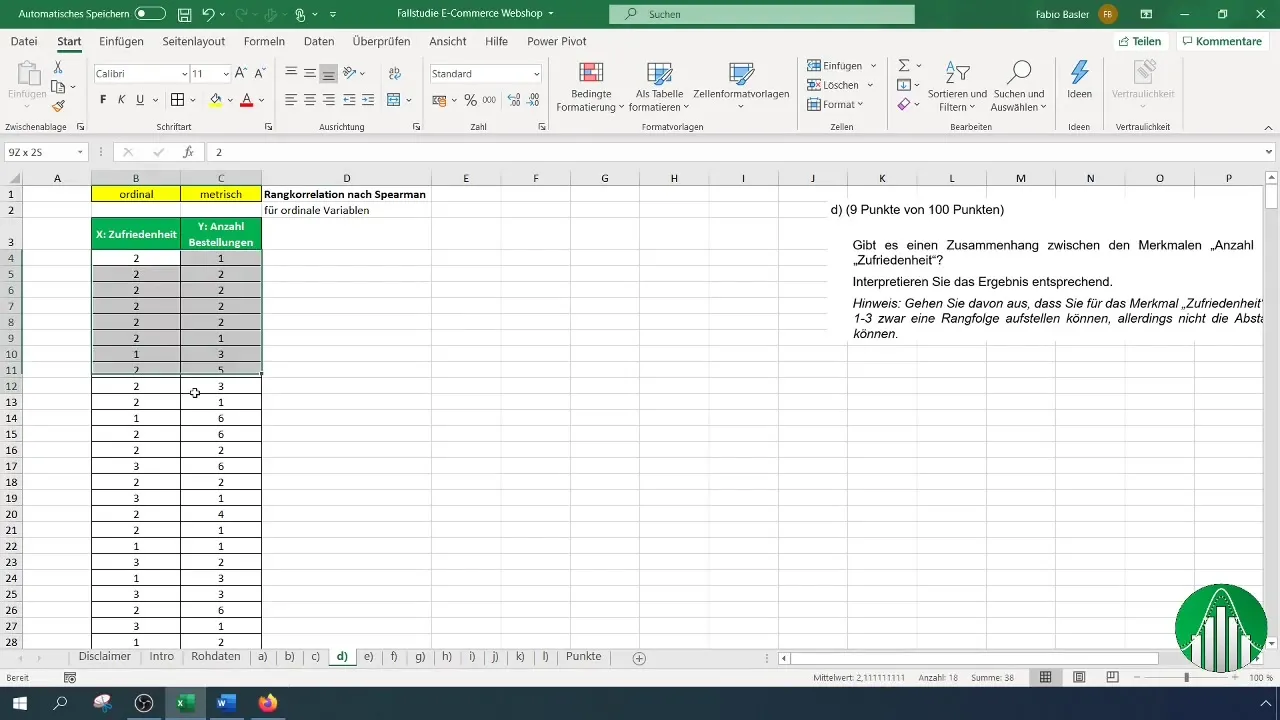
När du tillämpar denna formel, tänk på att markera kolumnen för nöjdhet och ställa in hela området från B4 till slutet av din data serie för att korrekt identifiera rangerna.
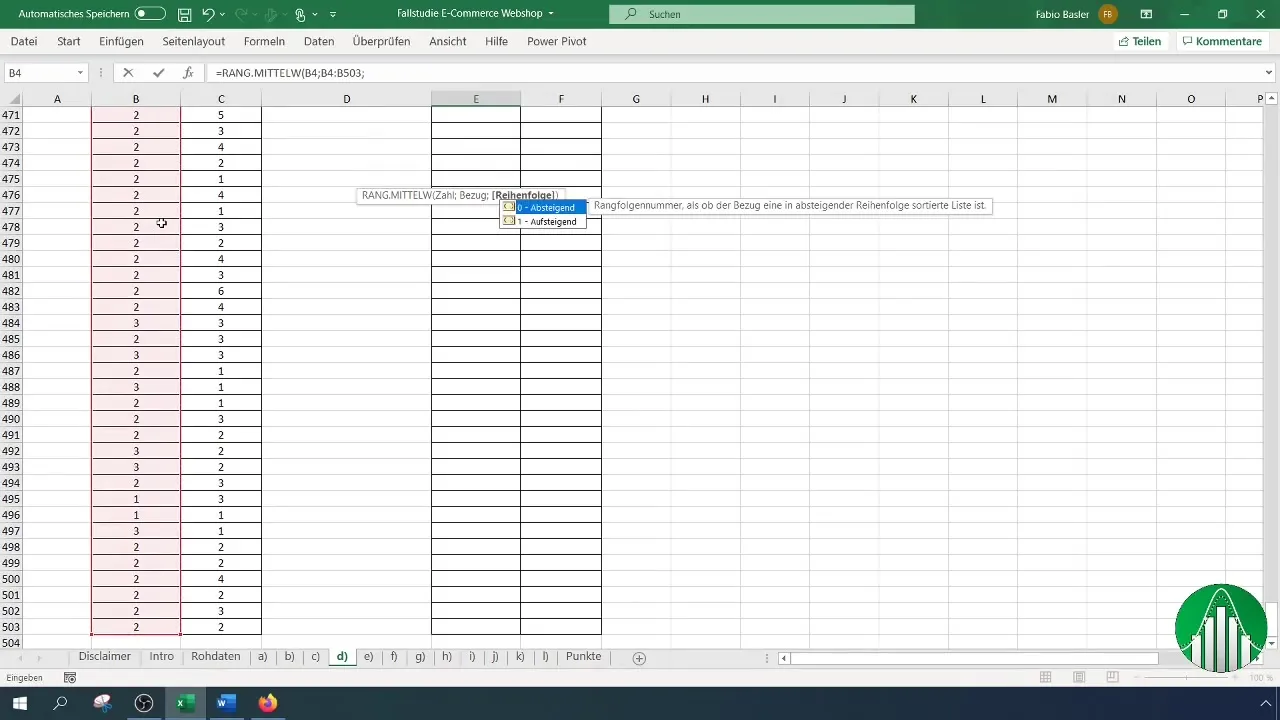
Bestäm om du vill sortera rangerna stigande eller fallande. Vanligtvis är det lämpligt att sortera dem stigande. Betona att cellreferenserna för rangerna ska vara fixerade genom att använda F4-tangenten. Detta är viktigt för att referenserna inte ska ändras under kopiering.
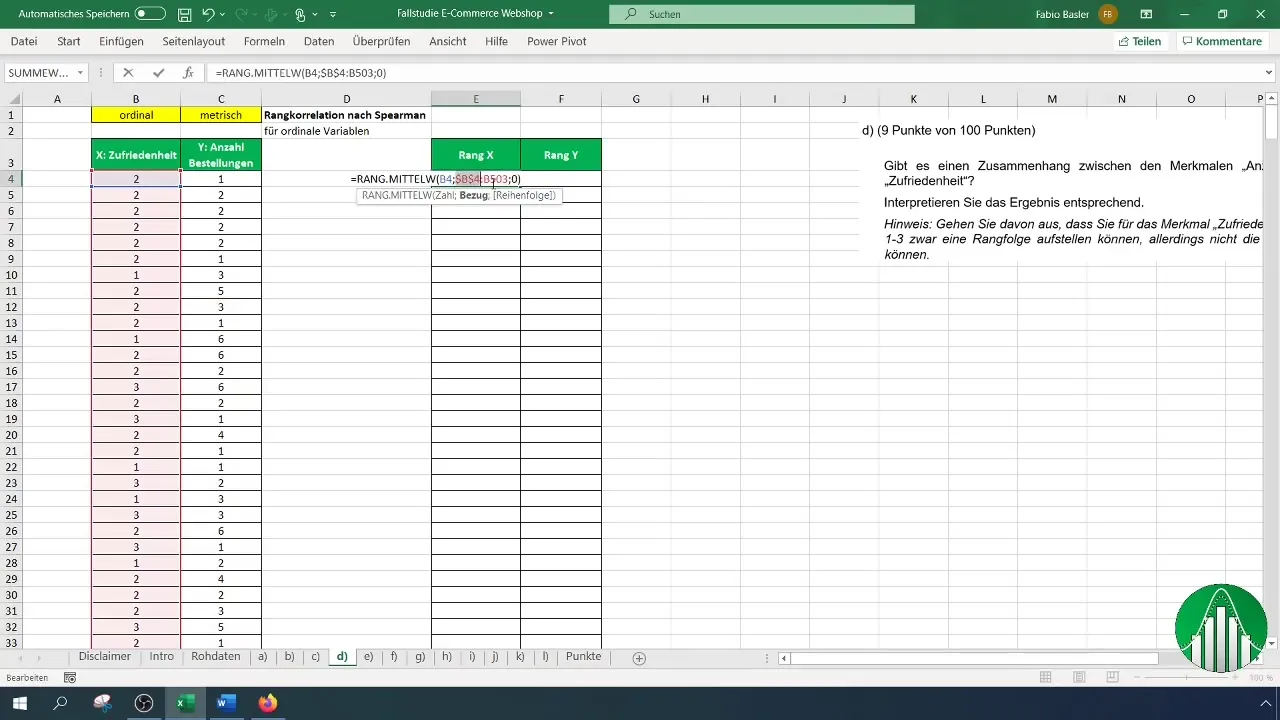
När du har bestämt rangerna för nöjdhet, upprepa processen för antalet beställningar. Se till att du korrekt tillämpar formeln och referensen.
Med båda ranglistorna (nöjdhet och antal beställningar) är du redo att beräkna Spearman-rankningskoefficienten. Använd formeln "=KORREL" för att bestämma förhållandet. Syntaxen ser ut på följande sätt:
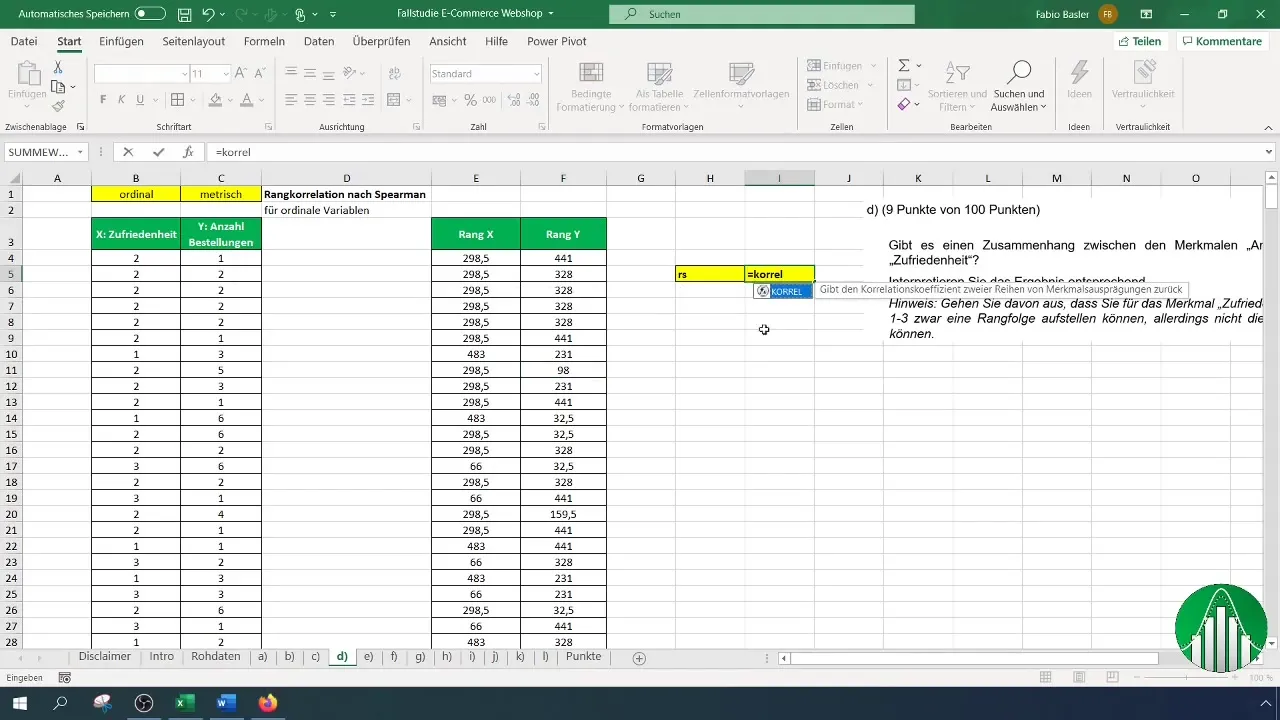
Ange ranglistan för nöjdhet för första referensen och ranglistan för beställningar för den andra referensen. Excel kommer automatiskt att beräkna Spearman's rankningskorrelationskoefficient.

Vad visar resultatet av din beräkning? Ett värde på 5,61% indikerar en svag positiv korrelation mellan nöjdhet och antalet beställningar. Detta innebär att det knappt finns något signifikant förhållande mellan dessa två variabler.
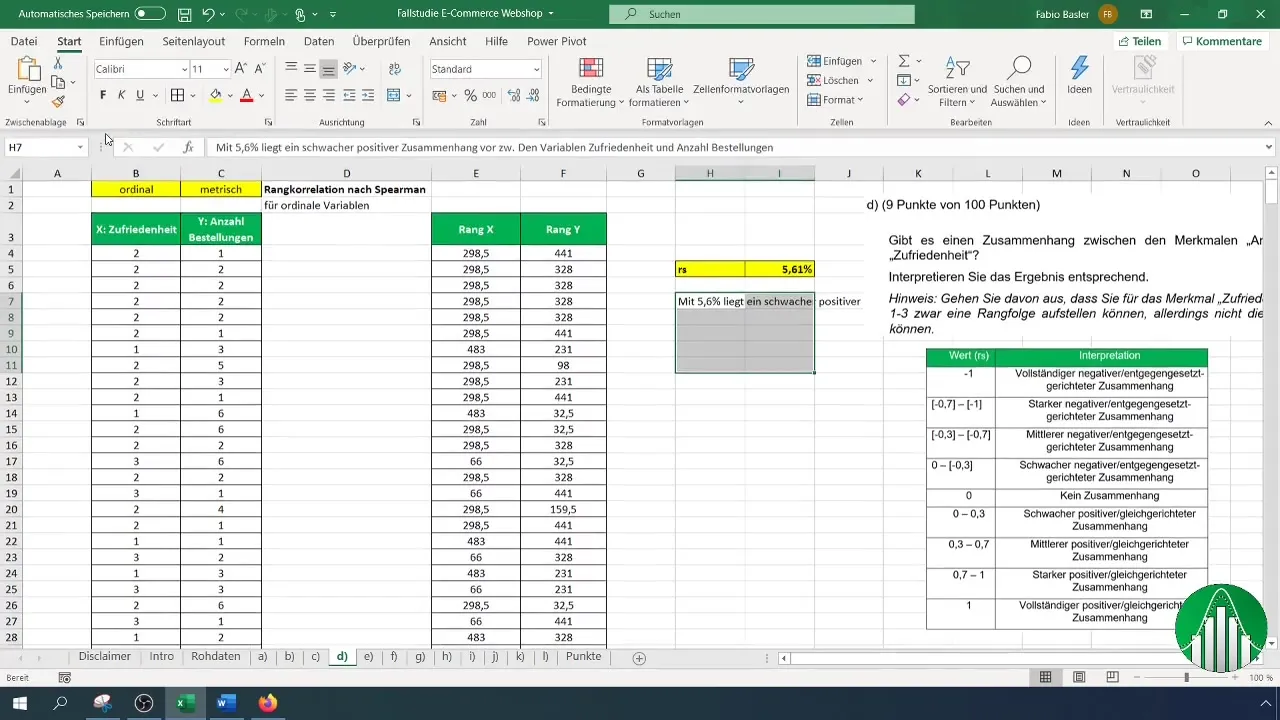
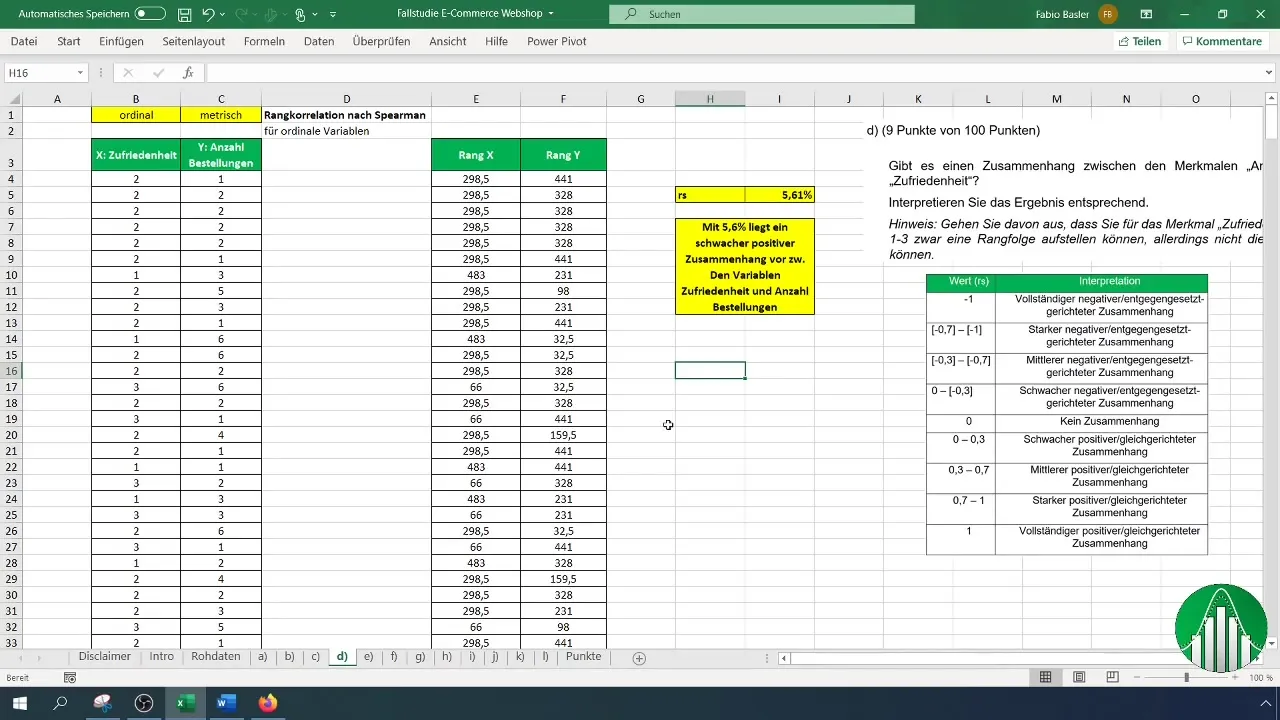
För att tolka dina resultat, använd en tabell med värden där olika områden av rangkorrelationen anges. Efter tolkning bekräftar vi att den låga korrelationsgraden innebär att variablerna är relativt oberoende av varandra.
Summering
Genom att utföra en rangkorrelationsanalys enligt Spearman i Excel kan du få värdefulla insikter om relationerna mellan ordinala och metriska variabler. Metoden är enkel att tillämpa och ger en klar bild av eventuella samband.
Vanliga frågor
Vad är Spearman rankkorrelationskoefficienten?Den Spearman rankkorrelationskoefficienten mäter styrkan och riktningen av en monoton relation mellan två variabler.
När är det meningsfullt att använda Spearman-koefficienten?Det är meningsfullt när minst en av variablerna är skalet i ordinal form.
Hur beräknar jag Spearman-koefficienten i Excel?Använd "Rang.Mittel"-funktionen för att bestämma rankerna och sedan "KORREL"-funktionen för att beräkna sambandet.
Vilket värdeintervall gäller för Spearman-koefficienten?Koefficienten ligger mellan -1 och 1. Värden nära 1 indikerar en stark positiv korrelation, medan värden nära -1 pekar på en stark negativ korrelation.
Vad kan ett värde på 5,61 % i rankkorrelationen betyda?Ett värde på 5,61 % indikerar en svag positiv relaterad, vilket tyder på att variablerna är relativt oberoende.


