Statistiska beräkningar är en oumbärlig del av dataanalysen, särskilt inom en e-handelsmiljö. Den historiska dataanalysen gör det möjligt att beräkna sannolikheter som är avgörande för företag. I den här guiden lär du dig hur du kan beräkna sannolikheter med hjälp av Poissonfördelningen i Excel, baserat på ett fallstudieexempel från en enkät.
Viktigaste insikter Poissonfördelningen gör det möjligt att bestämma sannolikheten för händelser som inträffar inom en fast tidsram. I detta exempel beräknar du sannolikheten att mer än två, men högst fyra kunder köper något i en e-handelsbutik inom en timme, samt sannolikheten att mer än två kunder totalt köper något.
Steg-för-steg-guide
Låt oss börja med att beräkna sannolikheterna för de beskrivna händelserna.
Steg 1: Förstå grunderna i Poissonfördelningen
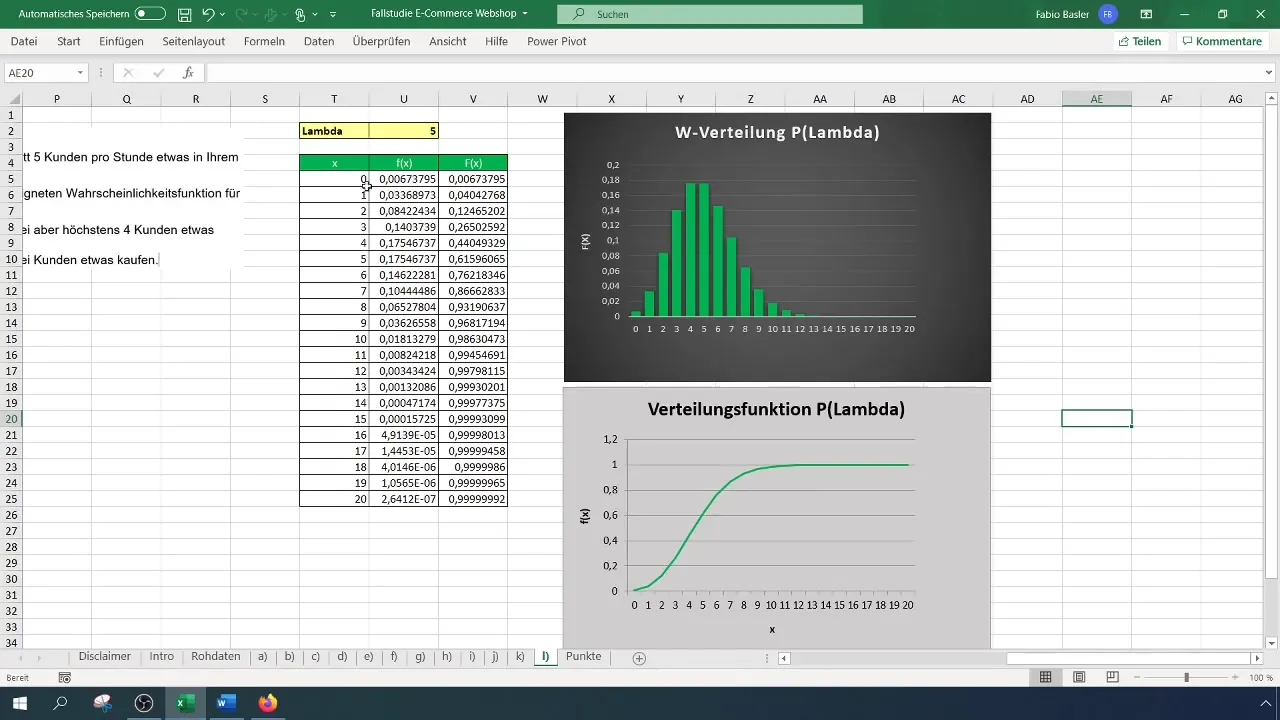
Först och främst är det viktigt att du förstår vad Poissonfördelningen är. Denna diskreta sannolikhetsfördelning används för att kvantifiera antalet händelser i fasta tidsperioder. I det aktuella exemplet har vi ett medelvärde på fem köp per timme. Detta formulerar du som ett lambdavärde (λ = 5).

Steg 2: Förbered data i Excel
Öppna Excel och förbered en ny tabell. Se till att du har de relevanta parametrarna (Lambda och antalet önskade händelser) tydligt synliga.
Steg 3: Bestäm sannolikhet för kundköp
För det första scenariot vill du beräkna sannolikheten att mer än två och högst fyra kunder köper något. För att göra detta måste du beräkna sannolikheterna för två och fyra kunder och sedan bestämma deras skillnad.

Steg 4: Använd Excel-formel för Poissonfördelning
Använd funktionen POISSON.VISSANNOLIKHET för att beräkna sannolikheterna. Formeln ser ut som följer:
- För två köpare: =POISSON.VISSANNOLIKHET(2; 5; SANT).
- För fyra köpare: =POISSON.VISSANNOLIKHET(4; 5; SANT).
Steg 5: Tolka resultat
Efter att ha tillämpat formlerna får du två sannolikheter, till exempel 12% för två kunder och 44% för fyra kunder. Sedan subtraherar du sannolikheten för två köpare från sannolikheten för fyra köpare, vilket ger dig en sannolikhet på 32% att mer än två men högst fyra kunder köper något.
Steg 6: Beräkna ytterligare sannolikheter
Nu handlar det om att beräkna sannolikheten att mer än två kunder köper i din e-handelsbutik. För att göra detta beräknar du först sannolikheten för exakt två köpare och subtraherar sedan detta resultat från 1.
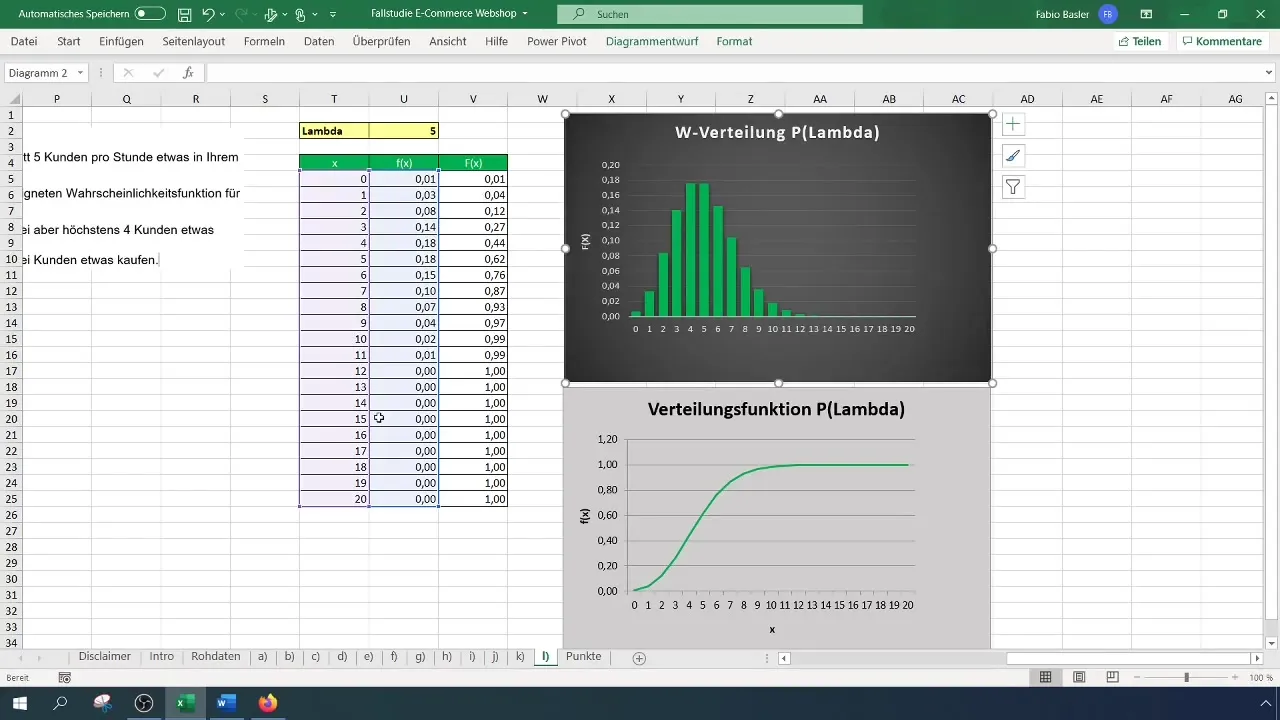
Steg 7: Använd Excel-formel för mer än två köpare
Excel-formeln är: =1 - POISSON.VISSANNOLIKHET(2; 5; SANT). Detta ger dig sannolikheten att mer än två kunder köper, vilket i detta fall är 88%.
Steg 8: Sammanfattning av resultat
Efter att du har utfört alla beräkningar, antecknar du de viktigaste sannolikheterna. Du har upptäckt att sannolikheten att mer än två, men högst fyra kunder beställer är 32%, medan sannolikheten att mer än två kunder totalt köper något är 88%.
Sammanfattning
I den här guiden har du lärt dig hur du använder Poissonfördelningen för att beräkna sannolikheter i Excel. Du har genomfört steg för att beräkna och tolka sannolikheter för specifika händelser.
Vanliga frågor
Vad är Poissonfördelningen?Poissonfördelningen är en diskret sannolikhetsfördelning som anger hur många gånger en händelse inträffar under en fastställd tidsperiod.
Hur beräknar jag sannolikheter med Poissonfördelningen i Excel?Du använder funktionen POISSON.VISSANNOLIKHET för att beräkna sannolikheter för olika värden.
Vad betyder ett lambdavärde på 5?Ett lambdavärde på 5 innebär att det genomsnittligt sker fem händelser (t.ex. köp) inom den definierade tidsramen (t.ex. en timme).
Vilka värden måste jag ange för Poissonfördelningen?Du måste ange antalet önskade händelser (x), medelvärdet (λ) och ange om du vill beräkna kumulativa sannolikheter.
Varför är Poissonfördelningen viktig för e-handel?Poissonfördelningen hjälper till att analysera köpmönster och förutse sannolikheten för kundaktiviteter, vilket kan stödja viktiga beslut inom marknadsföring och lagerhantering.


