Excel'de ortalama beklenen değerinin başarılı bir şekilde 1 tekil (single-point) testi

İstatistiksel Testler, veri analizinin ve karar vermenin merkezi bir parçasıdır. Özellikle biyoteknoloji alanında, ilaçların başarı oranları hakkında varsayımları test etmek hayati önem taşıyabilir. Bu kılavuz kapsamında, Excel'de beklenen varyansı bilinen bir Tek Örneklem Testi (1-SP Testi) nasıl verimli bir şekilde yaptığını öğreneceksin.

En Önemli Bulgular

Bu rehberde sana şunları öğreteceğiz:

• 1-SP Testinin teorik temelleri.
• Excel'de Testin Uygulanması Adımları.
• Sonuçların Yorumlanması.

Verilerin Hazırlanması

Excel'de 1-SP Testini uygulamak için öncelikle ilgili verilere ihtiyacın var. Örneğimizde, ilaçların başarı oranını analiz ettiğin bir durumdan bahsedelim. Ortalama başarı oranının daha önce %59 olduğu ve standart sapmanın 19 olduğu bilinmektedir. Verilerini Excel tablosuna girmen gerekecek.

Verilerinin sütunlara düzenlenmiş olmasına dikkat et, böylece daha sonra erişebilirsin. Her adımı daha kolay takip edebilmek için güzel bir düzenlilik önemli olacak.

Testin Genel Bakışı

1-SP Testi, ortalama başarı değerinin belirli bir değerden anlamlı şekilde farklı olup olmadığını kontrol etmek için kullanılır. Bu durumda %59'luk başarı oranının gelecekte belirgin biçimde artırılıp artırılamayacağını kontrol ediyoruz.

Varsayımlar Yapmak

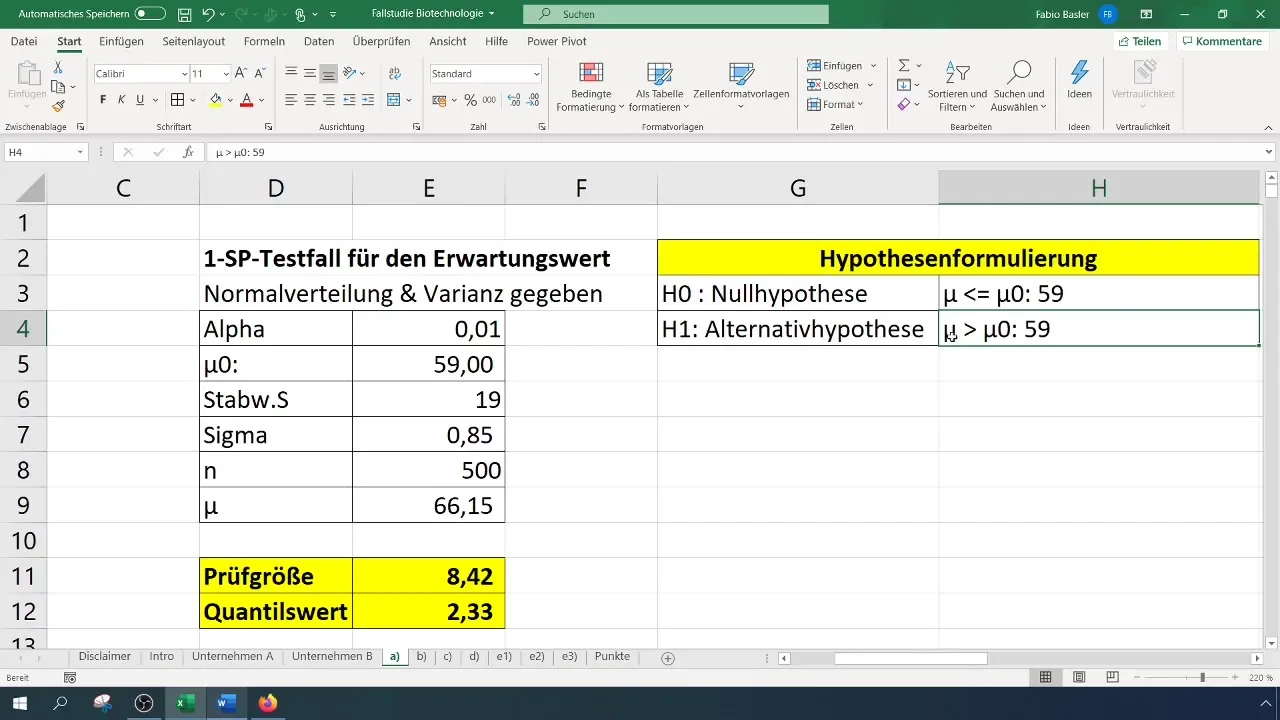
Test için yapacağın varsayımlar önemlidir:

• Boş Hipotez (H0): Gerçek beklenen değer 59'a eşittir (σ = %59).
• Alternatif Hipotez (H1): Gerçek beklenen değer 59%'dan büyüktür.

Hipotezleri formüle ederken, neyi doğrulamak zorunda olduğunu ve bu durumun bağlamında nasıl olduğunu odaklamalısın.

Boş hipotez ile alternatif hipotez arasındaki farkı net bir şekilde anlaman önemli, çünkü bu hesaplamaların temelini oluşturacaklar.

Örneklem Alımı

Testimiz için 500 ilacın bir örneğini alıyoruz. Örneklemin seçiminin temsiliyetinin olması ve sonuçlarınızın genel nüfusa gerçekçi bir şekilde aktarılabilmesini garanti etmek için uygun yöntemle olması önemlidir.

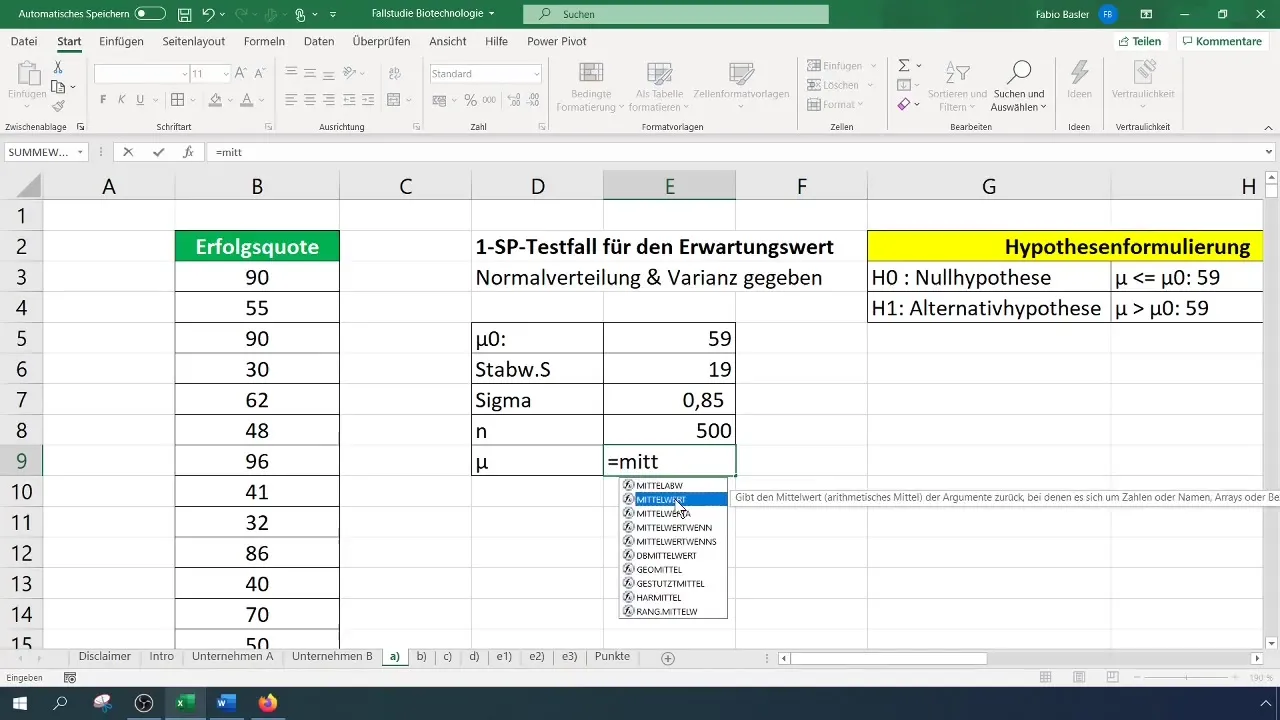
Test için ilk olarak aritmetik ortalamayı hesaplayacaksın. Bu, Excel'de ilgili formülü kullanarak kolayca yapılabilir.

Kontrol Değerinin Hesaplanması

1-SP Testi için kontrol değeri aşağıdaki formülle belirlenir:

[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]

Burada (\bar{x}) deneklerin ortalaması, (\mu_0) kabul edilen ortalama değeri (bu durumda 59), (\sigma) standart sapma (burada 19), ve (n) denek sayısı (500) olarak atanmıştır.

Formüle verdiğin değerleri yerine koyduktan sonra kontrol değerini hesaplayarak, anlamlı olup olmadığını belirle.

Kritik Değerin Belirlenmesi

%1 (0.01) anlamlılık seviyesi için kritik değeri okumalı veya hesaplamalısın. Bunun için Excel'de NORM.S.INV fonksiyonunu kullanabilirsin.

Formül şöyle:

[ \text{NORM.S.INV}(1 - \alpha) ]

Burada (\alpha) anlamlılık düzeyidir (0.01). Elde ettiğin değer, karşılaştırma yapmak için kontrol değerinin temelini oluşturacaktır.

Testin Yapılması

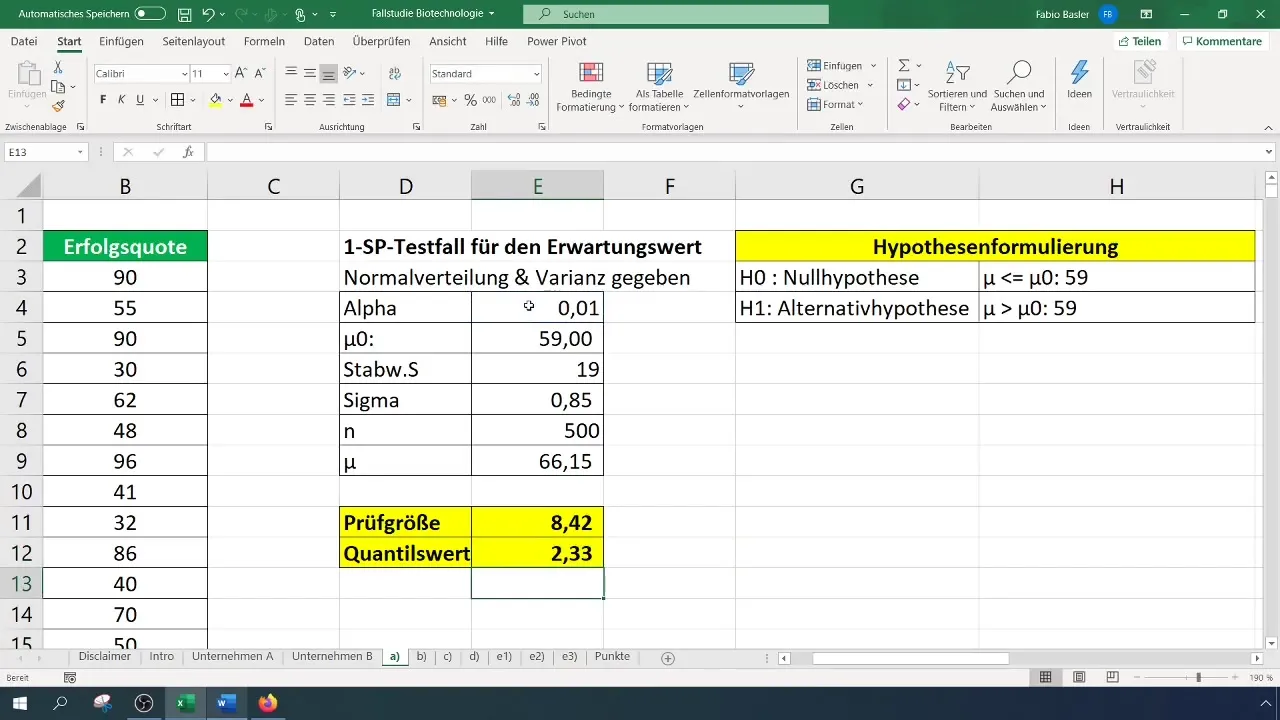
Şimdi hem kontrol değeri hem de kritik değere sahip olduktan sonra, ikisini karşılaştır:

• Test değeri, kritik değerden büyükse, boş hipotez reddedilir.
• Aksi takdirde, boş hipotezi reddedemezsin.

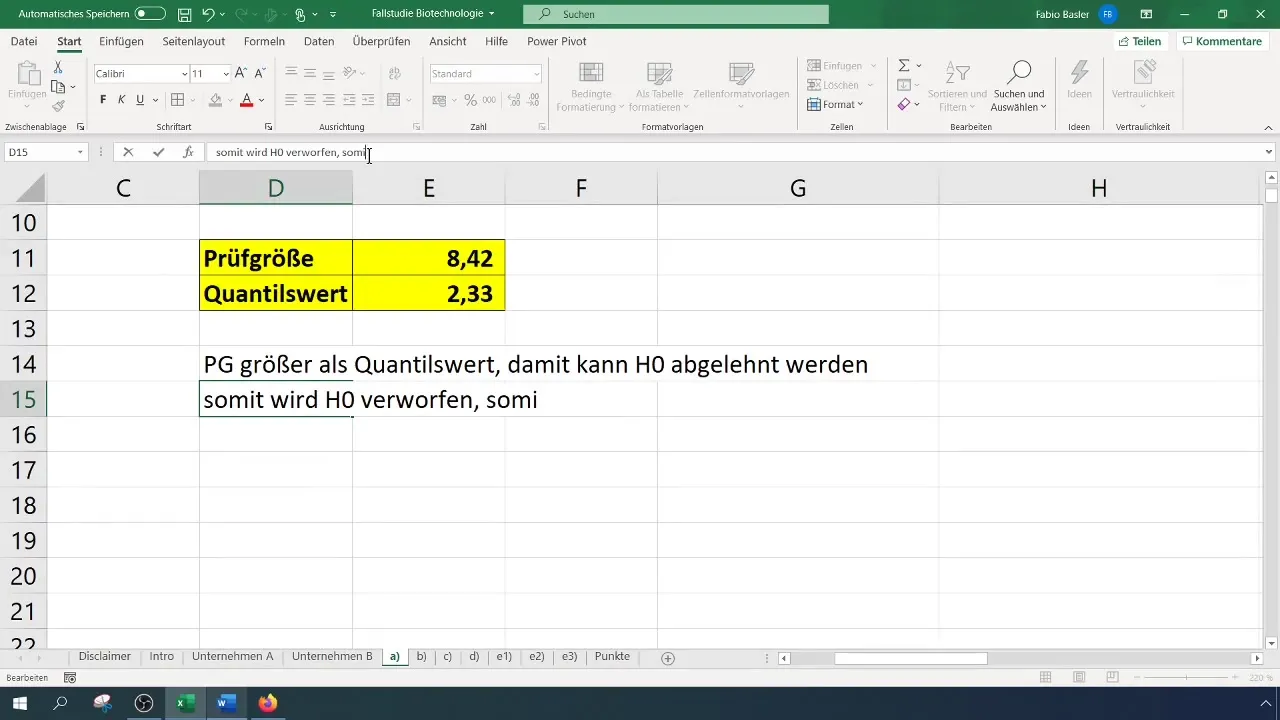
Bizim durumumuzda test istatistiği 8,4 olarak hesaplandı ve 2,33 olan kritik değeri aştı. Bu nedenle, nüll hipotezi reddedebiliriz. Bu, başarı oranının önemli ölçüde arttığını göstermektedir.

Sonuçların Yorumlanması

Testi gerçekleştirdikten ve sonuçları belirledikten sonra, net bir bağlamda yorumlamanız önerilir. Nüll hipotezin reddedilmesi, test edilen yeni değerin, bu durumda %59 olan geçmişten önemli ölçüde farklı olduğu anlamına gelir.

Bu bilgiler, şirketinizde stratejik karar verme süreci için son derece önemlidir. Başarı oranını artırmak için yapılan çabaların etkili olduğunu doğrulamaktadırlar.

Özet

Bu öğreticide, Excel'de beklenti değerine yönelik 1-SP testini nasıl gerçekleştireceğinizi öğrendiniz. Bir vaka çalışması üzerinden hipotez oluşturmadan, veri hesaplama ve sonuçları yorumlama adımlarını ayrıntılı bir şekilde görebileceksiniz. Bu bilgi notları sadece bilimsel analizler için değil, aynı zamanda kurumsal uygulamalar için de değerlidir.