İstatistiksel hipotez testleri, şirketlerin bilinçli kararlar vermek için vazgeçilmez bir araçtır. Aşağıdaki bölümde, Excel'de İki Örneklemli F-Testi'ni nasıl yapacağınızı göstereceğiz ve satış verilerinizin varyansı hakkındaki hipotezlerinizin geçerliliğini kontrol etmenize yardımcı olacağız. Bu kılavuz, öğrendiğiniz teknikleri güvenle uygulamanızı sağlayacak şekilde adım adım süreci izlemenizi sağlar.
En Önemli Bulgular
- İki Örneklemli F-Testi, iki veri grubunun varyanslarını karşılaştırmak için kullanılır.
- Amaç, mevcut satış verilerinin varyansının kabul edilen bir değerden farklı olup olmadığını test etmektir.
- Excel, gerekli hesaplamaları ve karşılaştırmaları yapmak için araçlar sunar.
Adım Adım Kılavuz
1. Veri Hazırlığı
Teste başlamadan önce verilerinizin hazırlandığından emin olun. Tüm ilgili verileri dikkate almak için filtreleri kaldırmak önemlidir. Verileri uygun sütunlarda seçmeye başlayın.

2. Parametrelerin Belirlenmesi
Testiniz için parametreleri tanımlayın. Kaç veri noktasını analiz ettiğinizi bilmelisiniz. Örneğimizde, analiz yapacağınız 100 satış rakamının normal dağılıma sahip olduğunu varsayalım.

3. Önceki Varyans Değerinin Belirlenmesi
Geçmişten bilinen varyans veya satış değeri analizinizde merkezi bir rol oynar. Bu örnekte, önceki değerin haftalık 116 milyon Euro olduğunu varsayalım.
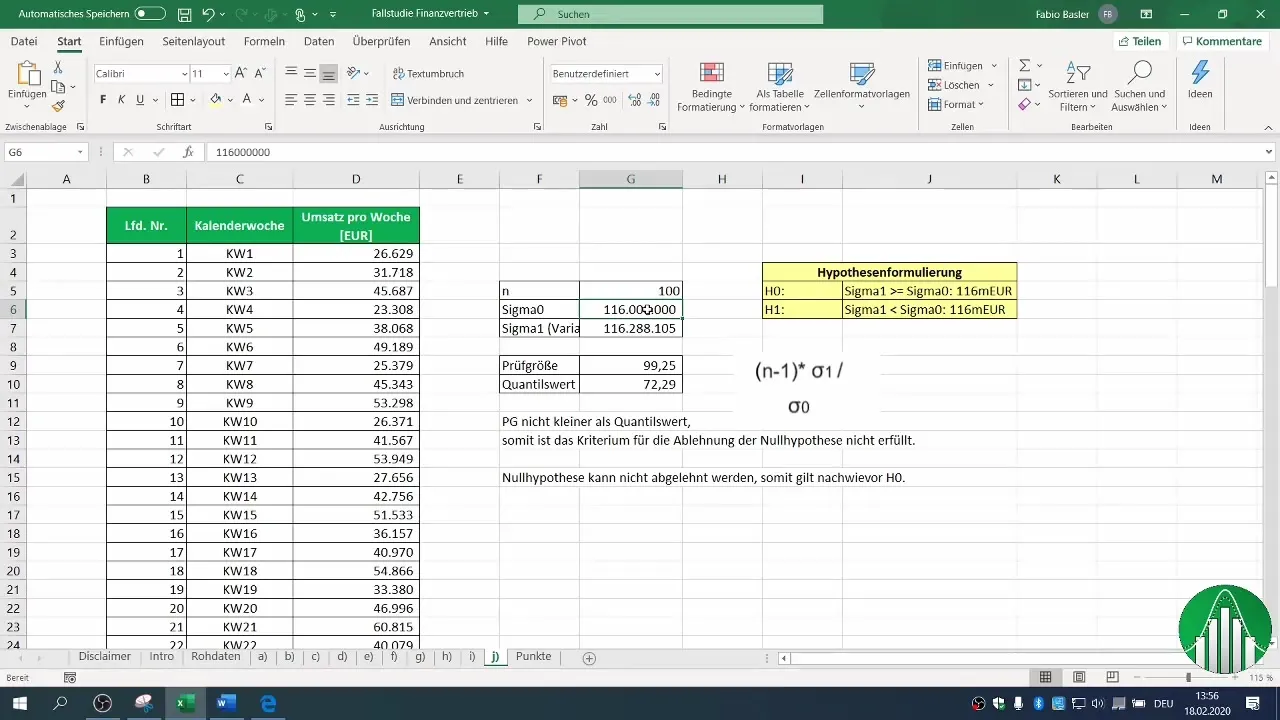
4. Hipotezlerin Formülasyonu
Boş hipotezinizi (H0) ve alternatif hipotezinizi (H1) formüle edin. Bu durumda, H0'un, varyansın 116 milyon veya daha fazla olmaya devam ettiğini, H1'in ise varyansın azaldığını varsaydığı bir durum oluştu.
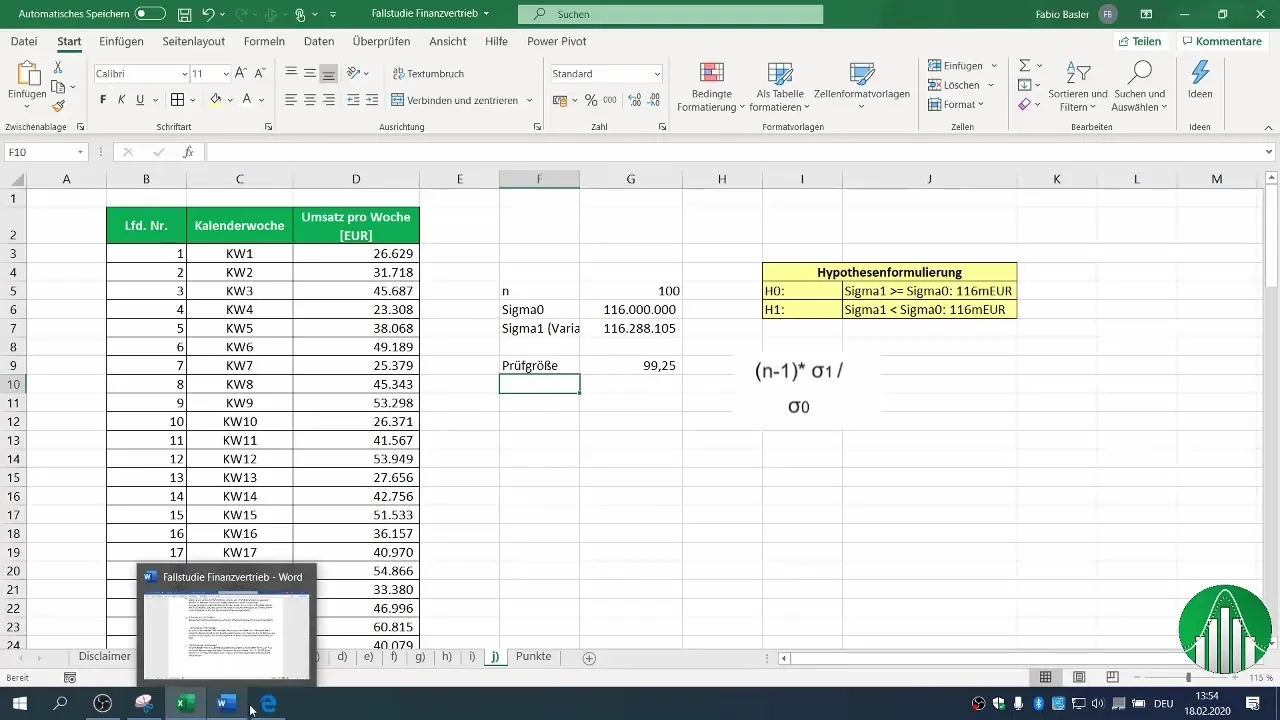
5. Test İçin Muayene Boyutunun Hesaplanması
Muayene boyutunu, örneklem varyansını kullanarak hesaplayabilirsiniz. Muayene boyutunuzun değerini belirlemek için gereken hesaplamaları yapın. Bu, şu formülle hesaplanır: (n-1) * σ1 / σ0, burada σ1 örneklem varyansınızı ve σ0 geçmişten gelen varyansı temsil eder.
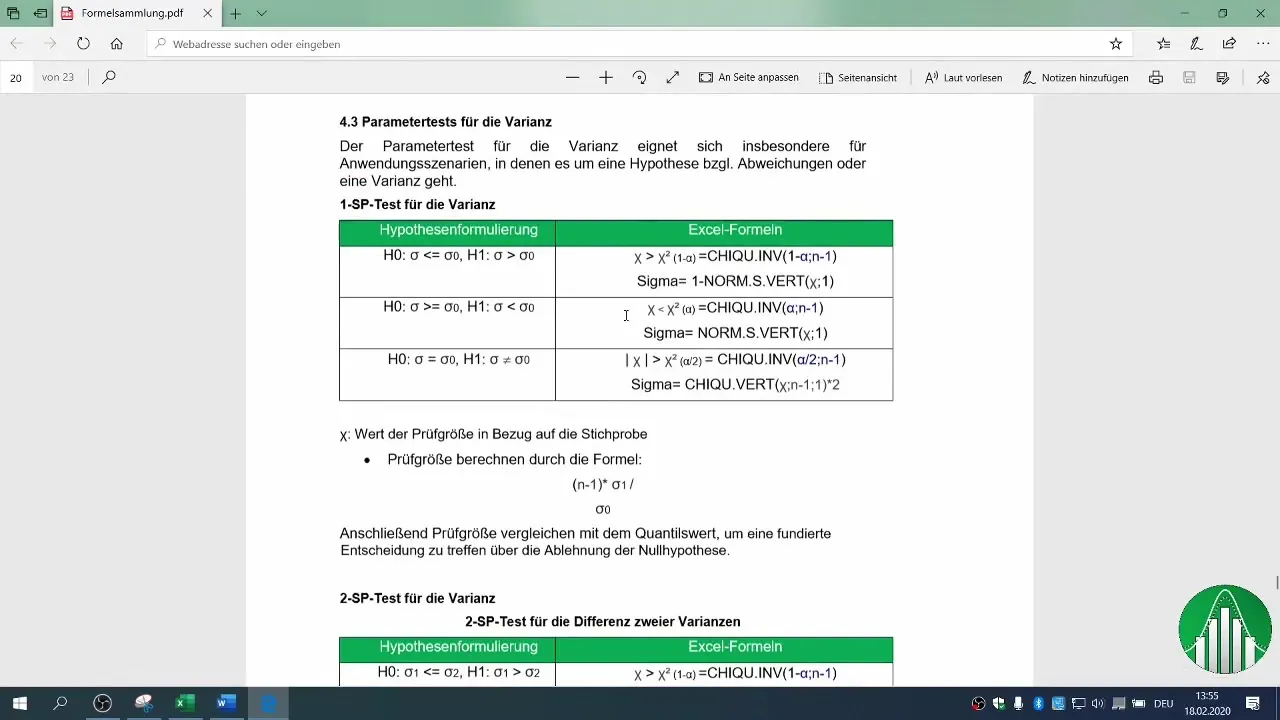
6. Kritik Bölgenin Belirlenmesi
Boş hipotezi reddedip edemeyeceğinizi belirlemek için kritik bölgeyi belirlemeniz gerekir. Güven aralığınız için Chi-Kare Dağılım Tablosunu kullanın. Örneğimizde %2 hata olasılığı kullandık.
7. Muayene Boyutunun ve kritik Büyüklüğün Karşılaştırılması
Hesaplanan muayene boyutunun kritik değerden küçük olup olmadığını kontrol edin. Bu durumda, muayene boyutumuzun kritik değerden küçük olmadığını belirledik.
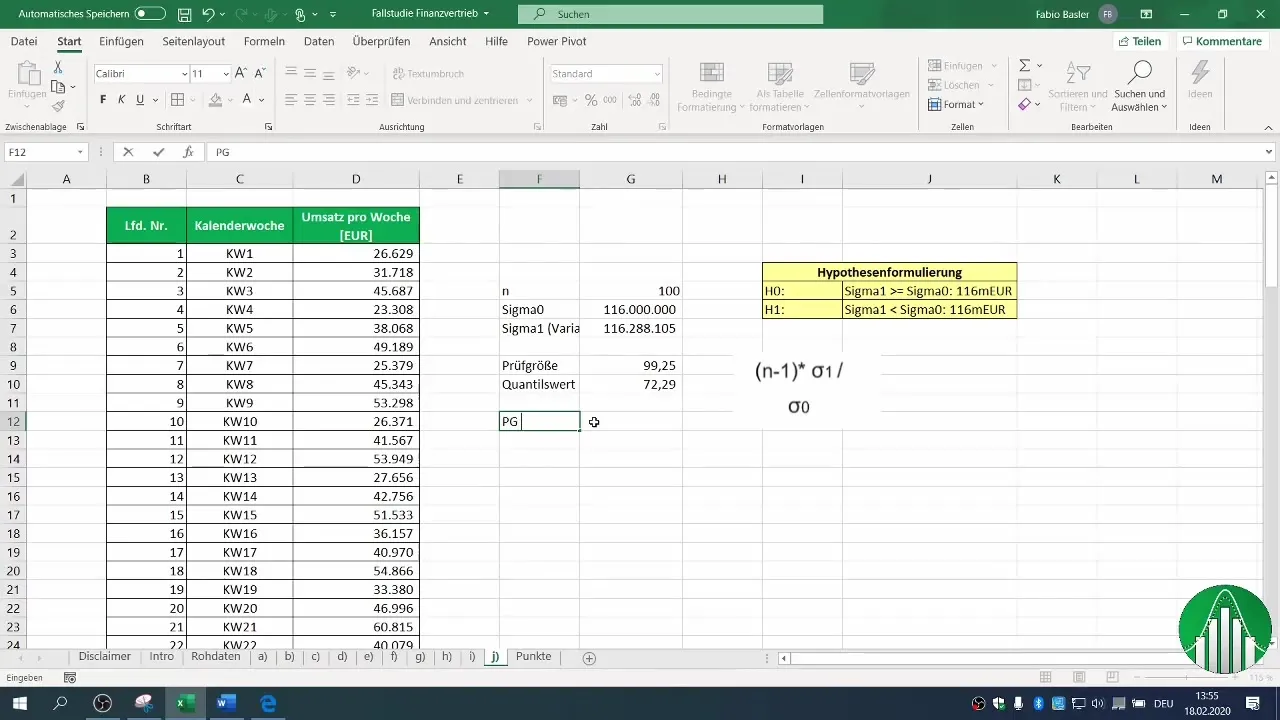
8. Sonuç Çıkarma
Karşılaştırmanıza dayanarak, boş hipotezinizi reddedip reddedemeyeceğinize karar verebilirsiniz. Bu örnekte, boş hipotezin reddedilemeyeceğini belirledik. Bu, satış verilerinizin varyansının hala kabul edilen değere veya belki de daha büyük olmaya devam ettiğini gösterir.
Özet
Bu kılavuzda, Excel'de İki Örneklemli F-Testi'ni nasıl yapabileceğinizi detaylı bir şekilde ele aldık. Verilerinizi nasıl hazırlayacağınızı, hipotezleri nasıl formüle edeceğinizi, muayene boyutunu nasıl hesaplayacağınızı, kritik bölgeyi nasıl belirleyeceğinizi ve son olarak sonuçlarınızı nasıl çıkaracağınızı öğrendiniz. Bu adımlarla, istatistiksel analizleri başarıyla gerçekleştirmek için kendinizi iyi donatmış durumdasınız.
Sık Sorulan Sorular
İki Örneklemli F-Testi nedir?İki Örneklemli F-Testi, iki veri grubunun varyanslarını karşılaştırmak için kullanılır.
F-Testi için hipotez nasıl formüle edilir?Boş hipotez, varyansın eşit veya daha büyük olduğunu belirtirken, alternatif hipotez azalma varsayar.
Testiniz için kritik değeri nasıl bulursunuz?Kritik değeri, güven aralığına ve serbestlik derecelerine dayanarak Chi-Kare tablolarından türetilebilir.
Boş hipotez reddedilemezse ne yapmalı?Bu, verilerin kabul edilen varyans değeriyle aynı olduğunu veya daha yüksek varyanslar sergilediğini gösterir.
Test için özel bir yazılıma ihtiyacım var mı?Veriler hazırlandığı sürece Excel, İki Örneklemli F-Test'i gerçekleştirmek için yeterlidir.

