Excel'de gelir için güven aralığını hesapla

Güven aralıklarının hesaplanması , özellikle bir örneklemden genel popülasyon hakkında çıkarımlar yapılması gerektiğinde, istatistiksel analizin temel bir parçasıdır. Bu kılavuzda, Excel'de bir anketin ortalama cirosu için çift yönlü bir güven aralığı nasıl hesaplanır​​ göstereceğim. Ham verilerden son güven aralığına ulaşmak için gereken farklı adımları öğrenecek ve bu metodolojiyi Excel'de nasıl uygulayacağınızı göreceksiniz.

En önemli bulgular

• Çift yönlü bir güven aralığı, belirli bir güven olasılığıyla gerçek ortalama cirosunun hangi sınırlar arasında olabileceğini belirtir.
• Hesaplama için ortalama, standart sapma, örneklem büyüklüğü ve ilgili t-kesitine ihtiyacınız olacaktır.
• Excel, bu değerleri hesaplamanızı ve güven aralığını görsel olarak temsil etmenizi sağlayacak gerekli işlevleri sunar.

Adım Adım Kılavuz

Adım 1: Verileri Hazırlama

İlk olarak, ilgili verileri Excel'de hazırlamanız gerekmektedir. Örneğe göre, normal müşterilere sadece bu grup için ortalama ciroyu hesaplamak istiyoruz.

Çalışma sayfanızdaki verileri işaretleyip kopyalayarak, bunları yeni bir alana yapıştırabilirsiniz. Bu, analizinizi ilgili müşteri grupları için filtrelemenize olanak tanır.

Adım 2: Temel Bilgiler Toplanıyor

Excel'de önemli tüm parametreleri içeren basit bir tablo oluşturun. Bunlar örneklem büyüklüğü (n), ortalama (x̄), standart sapma (σ) ve ilgili t-kesidi olacaktır. Normal bir dağılımı kabul ettiğimizi ve bir varyansımızın olmadığını zaten biliyoruz.

Adım 3: Örneklem Büyüklüğü (n) Hesapla

Normal müşteriler için gözlemlerin sayısını bulmak için ilgili verileri kesip =SAYIYI.SAY kullanarak sayıyı bulmalısınız. Bu durumda, filtrelenmiş verilerden 336 gözlem almanız gerekmektedir.

Adım 4: Ortalama (x̄) Hesaplama

Normal müşteriler için ciroların ortalamasını hesaplamak için =ORTALAMA formülünü kullanın. Bu size, örneğimizde 362,80 Euro olan normal müşteriler için ortalama ciroyu verecektir.

Adım 5: Standart Sapma (σ) Belirleme

Standart sapmayı hesaplamak için =SAPMA.S formülünü kullanın. Bu, indüktif istatistik için gereklidir, bu nedenle örneklem için standart sapmayı kullanıyoruz. Hesaplanan değer 123 Euro'dur.

Adım 6: Sigma (σ / √n) Hesaplama

Şimdi ortalamada standart sapmayı hesaplayarak, standart sapmayı örneklem büyüklüğünün kareköküne bölerek standart sapmayı hesaplayacaksınız. Formülü kullanın: =Standart Sapma/WURZEL(OBSC).

Adım 7: t-Kesidi Bulma

Bilinmeyen bir varyansa sahip bir normal dağılımımız olduğundan, t-kesidini belirlememiz gerekmektedir. Excel işlevi =T.INV.2T() 'yi kullanarak Alfa seviyesi (0,08) ​​ve serbest dereceler (n-1) belirterek t-değerini hesaplayın. Bu durumda, bu size 1,8 t-değerini verecektir.

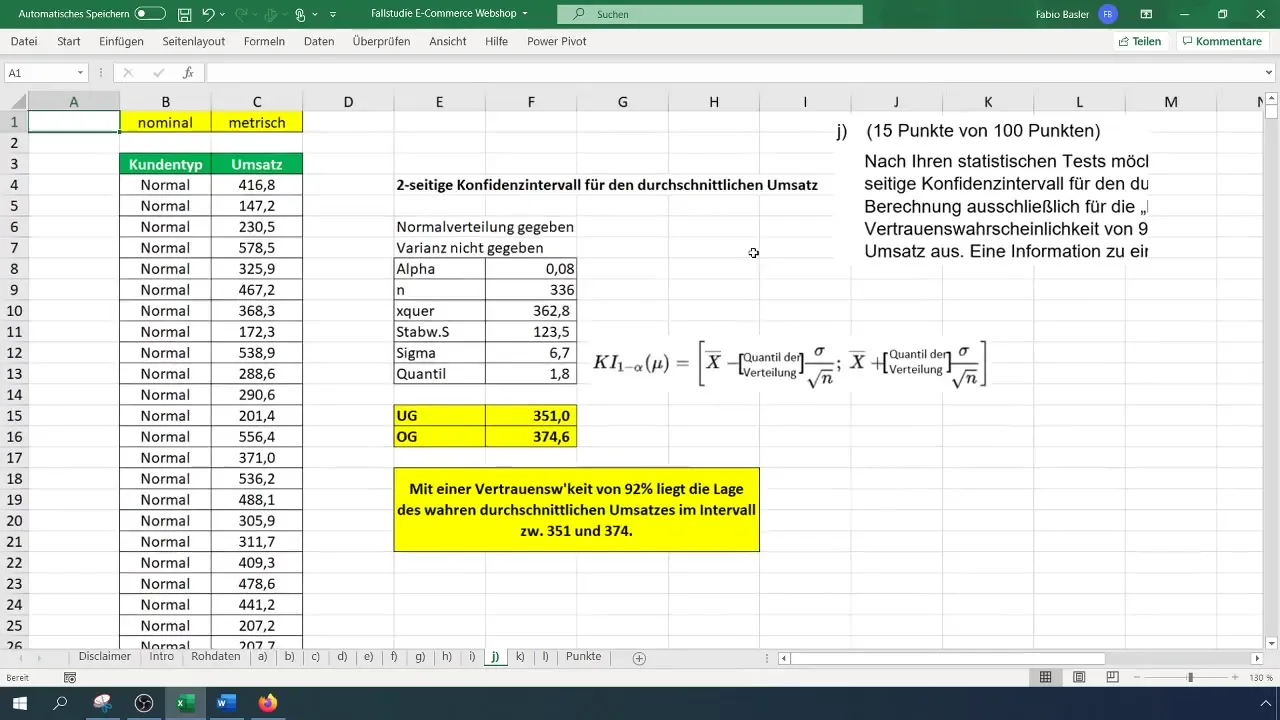
Adım 8: Güven Aralığının Alt Sınırını Hesaplama

Şimdi güven aralığının alt sınırını hesaplayın. Formül şöyle: =Ortalama - (t-Değeri * Sigma). Bu, örneğimizde 351 Euro olan alt sınırı size verecektir.

Adım 9: Güven Aralığının Üst Sınırını Hesaplama

Şimdi güven aralığının üst sınırını hesaplayabilirsiniz. Formül benzerdir, ancak bu sefer t-Değeri'ni ortalamanıza ekleyin: =Ortalama + (t-Değeri * Sigma). Bu durumda üst sınır 374 Euro olacaktır.

Adım 10: Güven Aralığının Görselleştirilmesi

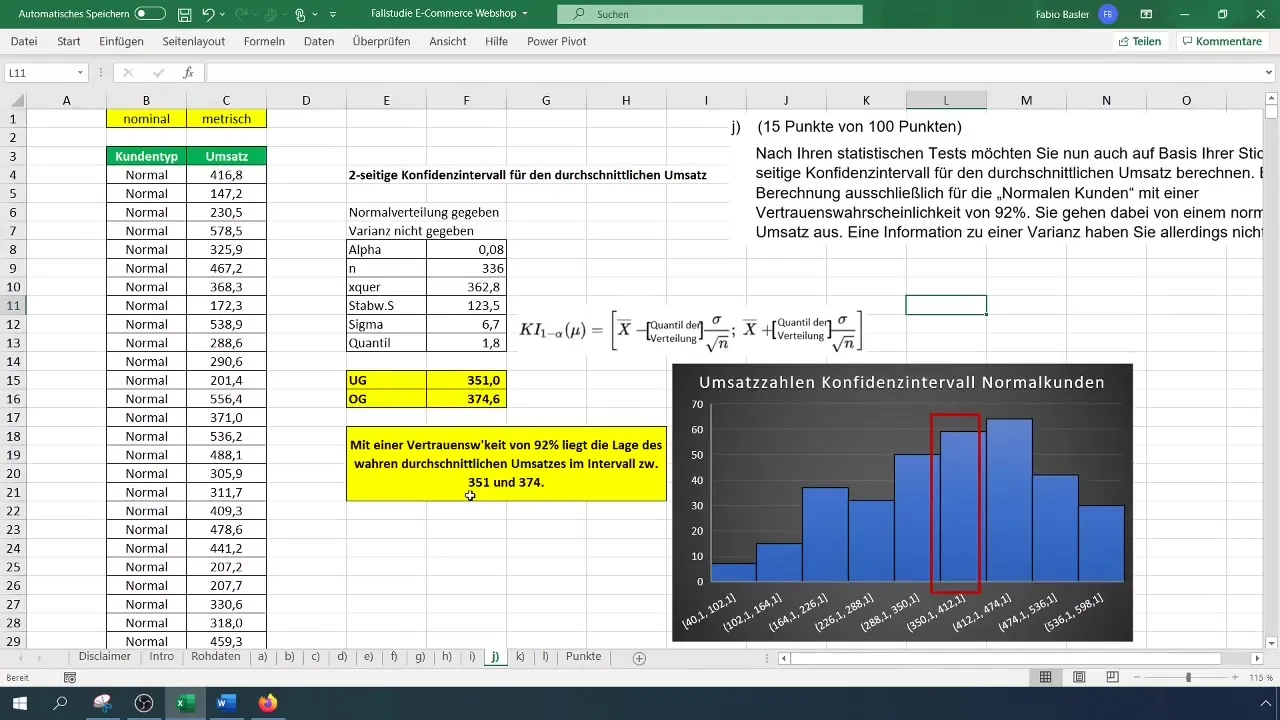
Sonuçlarınızı görselleştirmek için Excel'de bir histogram oluşturabilir ve güven aralığını işaretleyebilirsiniz. Gerçek ortalama müşteri cirosunun, %92 güven olasılığıyla hangi aralıkta olduğunu göstermek için alt ve üst sınır arasında bir çizgi çizin.

Adım 11: Yorum ve Sonuç

Artık normal müşterilerin gerçek ortalama gelirinin 351 ile 374 Euro arasında, %92 güvenilirlik olasılığıyla olduğunu belirleyebilirsin. Bu, şirketindeki diğer kararlar için önemlidir.

Özet

Bu kılavuzda Excel'de ortalama geliri için çift yönlü bir güven aralığının nasıl hesaplanacağını öğrendin. Veri hazırlığından grafiksel temsile ve sonuçların yorumlanmasına kadar tüm gerekli adımları tamamladın.