İstatistiksel Hesaplamalar, özellikle e-ticaret ortamlarında veri analizinin vazgeçilmez bir parçasıdır. Tarihsel veri analizi, şirketler için hayati olan olasılıkları belirlemenizi sağlar. Bu kılavuzda, bir anket örneğine dayanan Poisson dağılımını kullanarak Excel'de olasılıkları nasıl hesaplayabileceğinizi öğreneceksiniz.
En Önemli Tespitler Poisson dağılımı, sabit bir zaman çerçevesinde meydana gelen olayların olasılığını belirlemenizi sağlar. Bu örnekte bir saat içinde e-ticaret mağazasında iki ila dört müşterinin bir şey satın alması olasılığını ve toplamda iki müşterinin bir şey satın alması olasılığını hesaplayacaksınız.
Adım Adım Kılavuz
Belirtilen olaylar için olasılıkları hesaplama işlemine başlayalım.
Adım 1: Poisson Dağılımının Temellerini Anlama
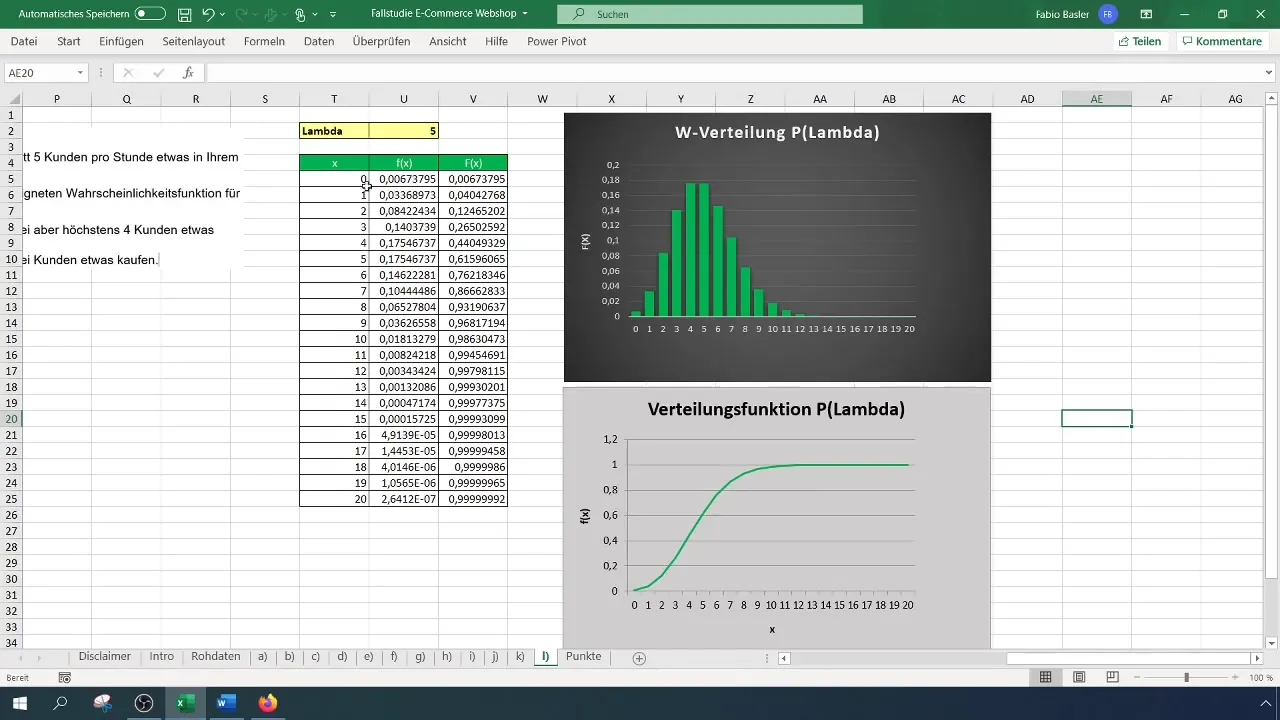
İlk olarak, Poisson dağılımının ne olduğunu anlamanız önemlidir. Bu ayrık olasılık dağılımı, sabit zaman aralıklarında meydana gelen olayların sayısını nicelendirmek içindir. Bu örnekte saatte beş satın alma ortalamamız var. Bu ortalamayı Lambda değeri olarak formüle edersiniz (λ = 5).

Adım 2: Excel'de Verileri Hazırlama
Excel'i açın ve yeni bir tablo hazırlayın. İlgili parametreleri (Lambda ve istenen olay sayısı) net bir şekilde görebildiğinizden emin olun.
Adım 3: Müşteri Satın Alma Olasılıklarını Belirleme
İlk senaryo için iki ile dört arasında müşterinin bir şey satın alması olasılığını hesaplamak istiyorsunuz. Bunun için iki ve dört müşteri için olasılıkları hesaplamalı ve ardından farklarını bulmalısınız.

Adım 4: Poisson Dağılımı İçin Excel Formülü Kullanma
Olasılıkları hesaplamak için POISSON.WAHRSCHEINLICHKEIT işlevini kullanın. Formül şu şekildedir:
- İki alıcı için: =POISSON.WAHRSCHEINLICHKEIT(2; 5; WAHR).
- Dört alıcı için: =POISSON.WAHRSCHEINLICHKEIT(4; 5; WAHR).
Adım 5: Sonuçları Yorumlama
Formülleri uyguladıktan sonra, örneğin iki müşteri için %12 ve dört müşteri için %44 gibi iki olasılık elde edersiniz. Şimdi iki alıcı için, dört alıcı için olan olasılığı çıkararak, iki ile dört arasında müşterinin bir şey satın alması olasılığınızın %32 olduğunu bulacaksınız.
Adım 6: Diğer Olasılıkları Hesaplama
Şimdi, e-ticaret mağazanızda iki müşteriden fazlasının alışveriş yapma olasılığını hesaplamanın zamanı geldi. Bunun için önce tam olarak iki alıcı için olasılığı hesaplar ve bu sonucu 1'den çıkarırsınız.
Adım 7: Daha Fazla İki Alıcı İçin Excel Formülü Kullanma
Excel formülü şu şekildedir: =1 - POISSON.WAHRSCHEINLICHKEIT(2; 5; WAHR). Bu size, iki müşteriden fazlasının bir şeyler alacağı olasılığı veren %88'lik bir sonuç sağlar.
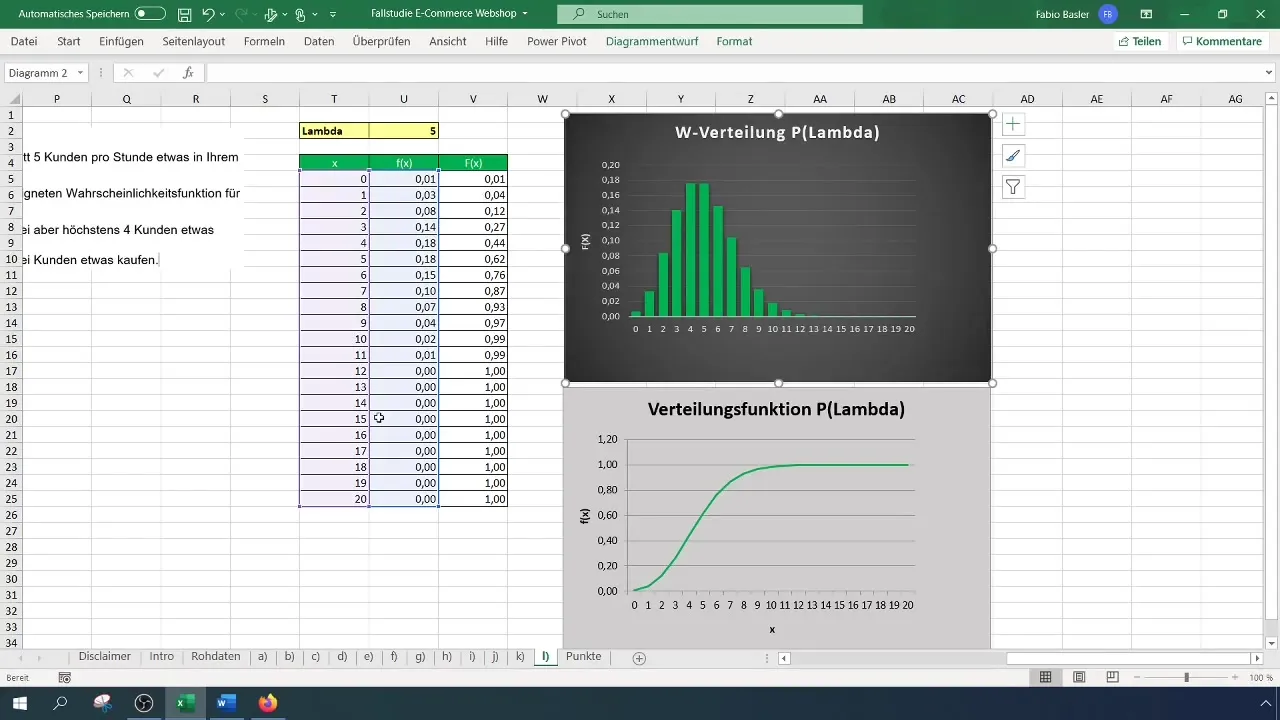
Adım 8: Sonuçlarının Özeti
Tüm hesaplamaları yaptıktan sonra, temel olasılıkları kaydedersiniz. İki ile dört arasında müşterinin bir şey satın alacağı olasılığın %32, iki müşteriden fazlasının toplamda bir şey alması olasılığının ise %88 olduğunu belirlediniz.
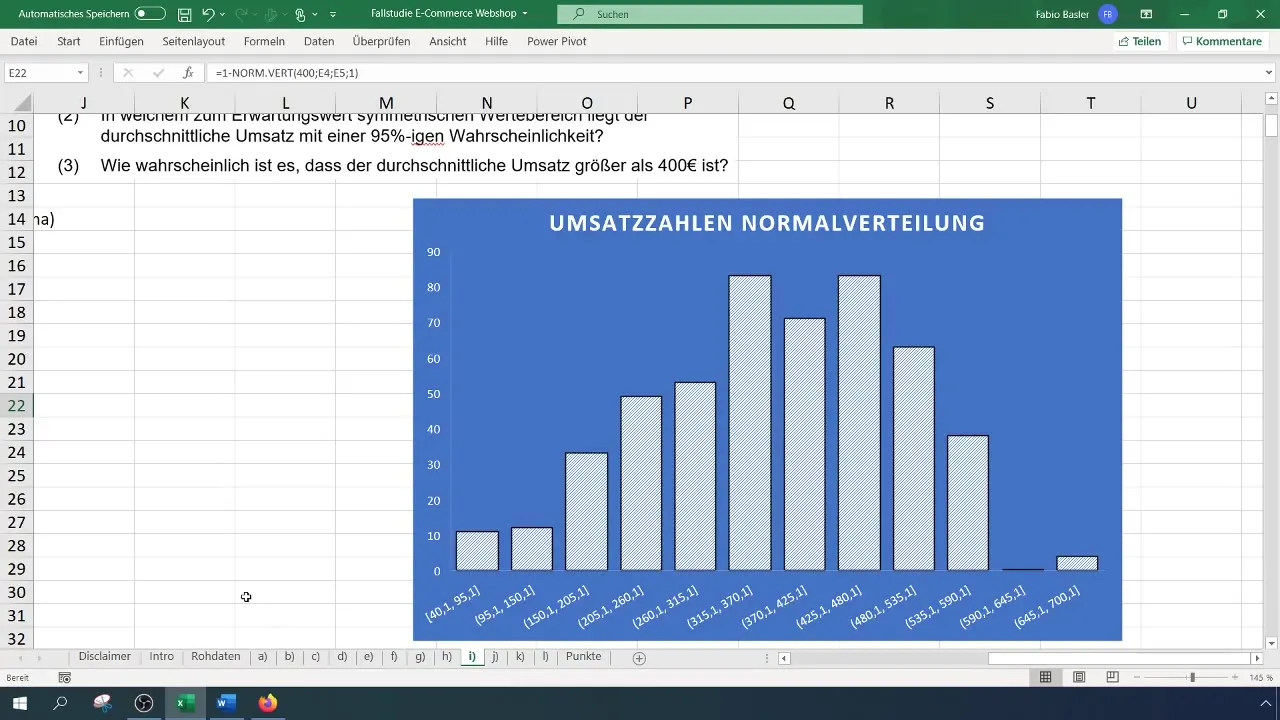
Özet
Bu kılavuzda, Excel'de olasılıkların hesaplanmasında Poisson dağılımını nasıl kullanabileceğinizi öğrendiniz. Belirli olaylar için olasılıkları hesaplamak ve yorumlamak için adımlar attınız.
Sık Sorulan Sorular
Poisson dağılımı nedir?Poisson dağılımı, sabit bir zaman diliminde bir olayın kaç kez meydana geldiğini gösteren ayrık bir olasılık dağılımıdır.
Excel'de Poisson dağılımını kullanarak nasıl olasılıkları hesaplarım?Farklı değerler için olasılıkları hesaplamak için POISSON.WAHRSCHEINLICHKEIT fonksiyonunu kullanırsınız.
5 Lambda değeri ne anlama geliyor?5 Lambda değeri, belirli bir zaman diliminde (örneğin bir saatte) ortalama beş olayın (örneğin satın almalar) gerçekleşeceğini gösterir.
Poisson dağılımı için hangi değerleri belirtmem gerekir?İstenen olay sayısını (x), ortalama (λ) ve kümülatif olasılıkları hesaplamak isteyip istemediğinizi belirtmelisiniz.
Poisson dağılımı neden e-ticaret için önemlidir?Poisson dağılımı, alışveriş modellerini analiz etmeye ve müşteri aktivitelerinin olasılığını tahmin etmeye yardımcı olarak pazarlama ve stok yönetiminde önemli karar desteklerinde bulunur.


