Статистичні тести є ключовою частиною аналізу даних та процесу прийняття рішень. Особливо в області біотехнології може бути вирішальним перевірка гіпотез щодо відсотку успішності лікарських засобів. В рамках цього посібника ви дізнаєтеся, як ефективно виконати тест на одній вибірці (тест 1-SP) для математичного сподівання з відомою дисперсією в Excel.
Найважливіші відомості
Цей посібник допоможе вам зрозуміти:
- Теоретичні основи тесту на одній вибірці.
- Етапи виконання тесту в Excel.
- Інтерпретація результатів.
Підготовка даних
Для виконання тесту на одній вибірці в Excel спочатку вам потрібні відповідні дані. Наприклад, ми розглядатимемо ситуацію, де ви аналізуєте відсоток успішних лікарських засобів. Відомо, що середній відсоток успіху раніше становив 59%, а стандартне відхилення було 19. Спочатку вам слід ввести ваші дані у таблицю Excel.
Переконайтеся, що ваші дані організовані у стовпці, щоб пізніше мати до них доступ. Гарне представлення допоможе вам легше прослідковувати окремі кроки.
Огляд тесту
Тест на одній вибірці призначений для перевірки, чи середнє значення успіху значно відрізняється від заданого значення. У цьому випадку ми перевіряємо, чи в майбутньому відсоток успіху 59% може бути значно підвищений.
Формулювання гіпотез
Сформульовані вами гіпотези для тесту мають важливе значення:
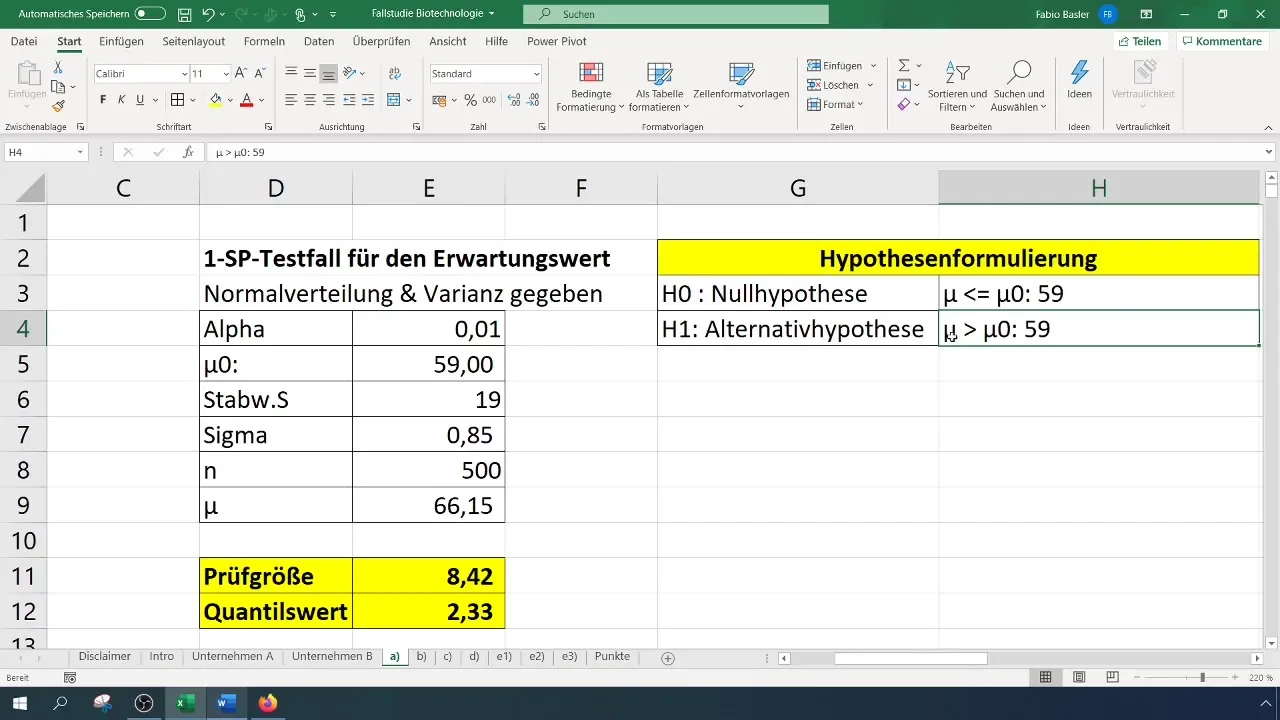
- Нульова гіпотеза (Н0): Реальне математичне сподіване значення дорівнює 59 (σ = 59%).
- Альтернативна гіпотеза (Н1): Реальне математичне сподіване значення більше за 59%.
При формулюванні гіпотез важливо зрозуміти, що саме потрібно перевірити та як це проявляється у вашому контексті.
Важливо чітко розрізняти між нульовою гіпотезою та альтернативною гіпотезою, оскільки вони є основою для наступних обчислень.
Збір вибірки
Для нашого тесту ми беремо вибірку з 500 лікарських засобів. Важливо помітити, що вибірка повинна бути репрезентативною і має гарантувати відображення результатів на загальну популяцію за допомогою відповідного методу.
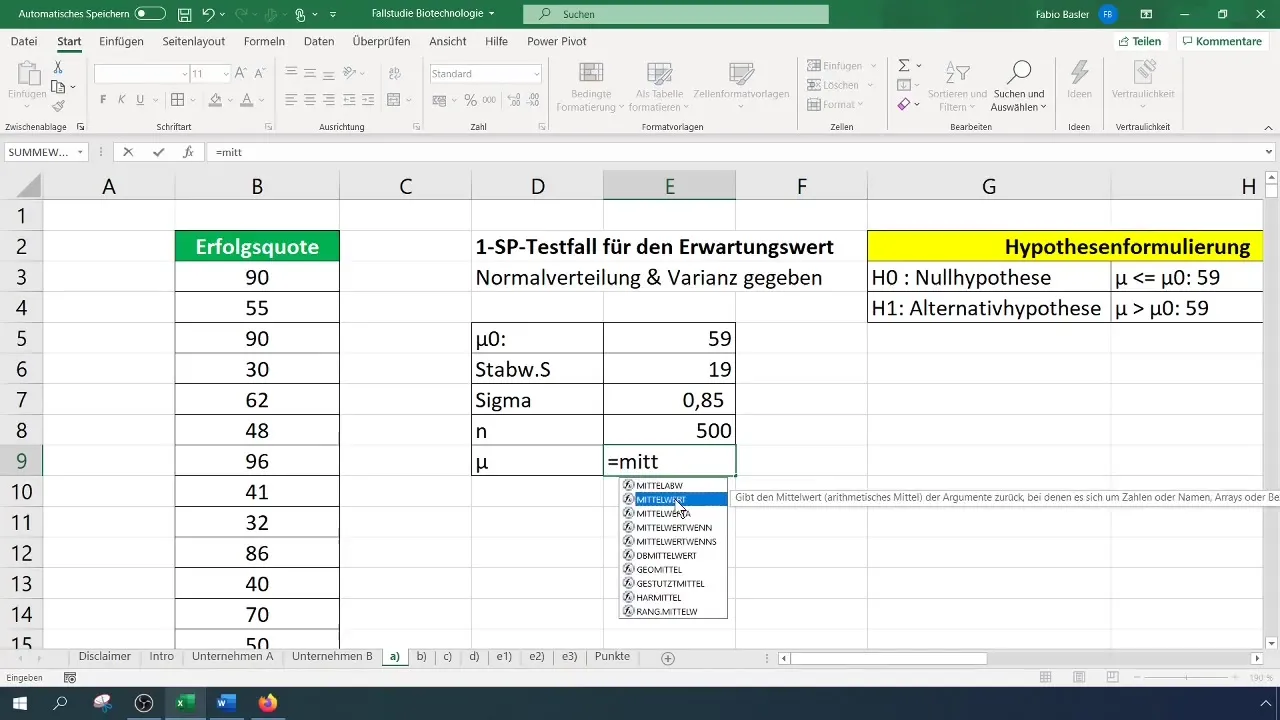
Для тесту ви починаєте з обчислення середнього арифметичного. Це можна легко зробити, використовуючи в Excel відповідну формулу.
Обчислення критичного значення
При обчисленні критичного значення для тесту на одній вибірці використовується наступна формула:
[ Z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} ]
Тут (\bar{x}) - середнє значення вашої вибірки, (\mu_0) - припущене середнє значення (у цьому випадку 59), (\sigma) - стандартне відхилення (тут 19), а (n) - кількість вибірок (500).
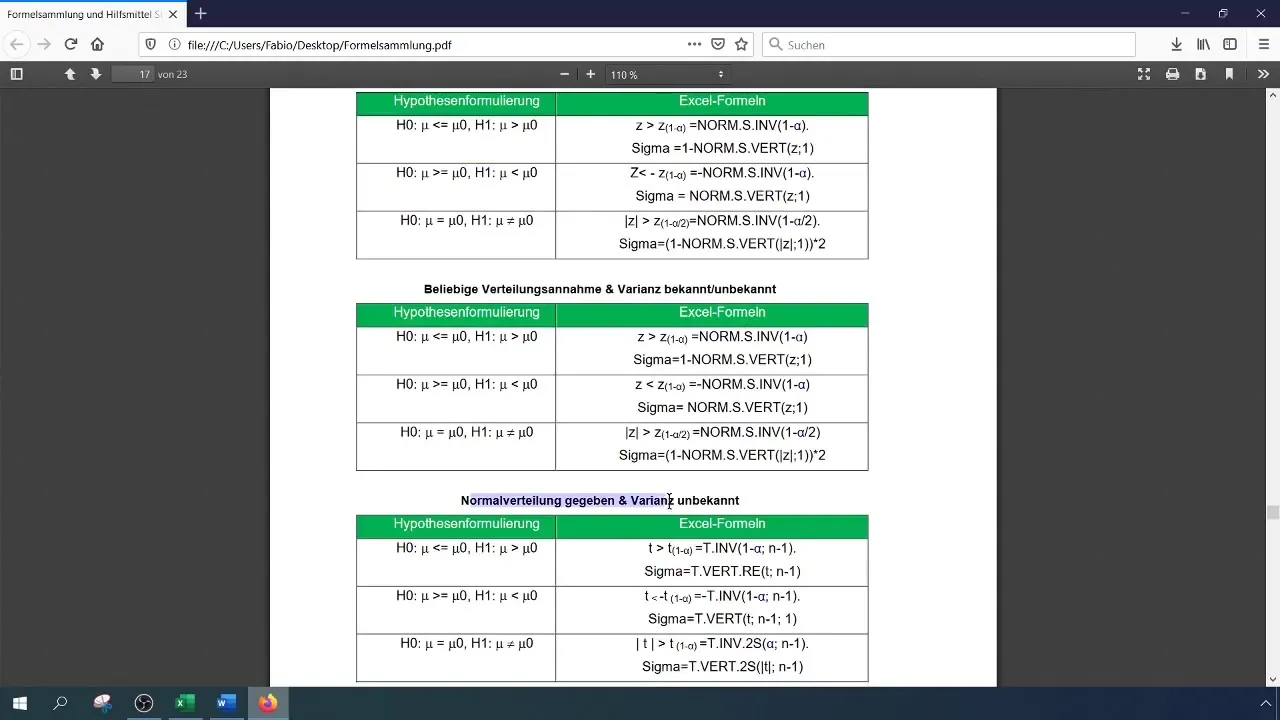
Після введення значень у формулу, обчисліть критичне значення, щоб визначити, чи воно є значущим, чи ні.
Визначення критичного значення
Для рівня значущості 1% (0,01) вам потрібно визначити або обчислити критичне значення. Це можна зробити в Excel за допомогою функції NORM.S.INV.
Формула має вигляд:
[ \text{NORM.S.INV}(1 - \alpha) ]
Тут (\alpha) - рівень значущості (0,01). Отримане значення буде використано для порівняння з критичним значенням.
Виконання тесту
- Якщо пробна величина більша за критичне значення, нульову гіпотезу відкидають.
- В іншому випадку ви не можете відхилити нульову гіпотезу.
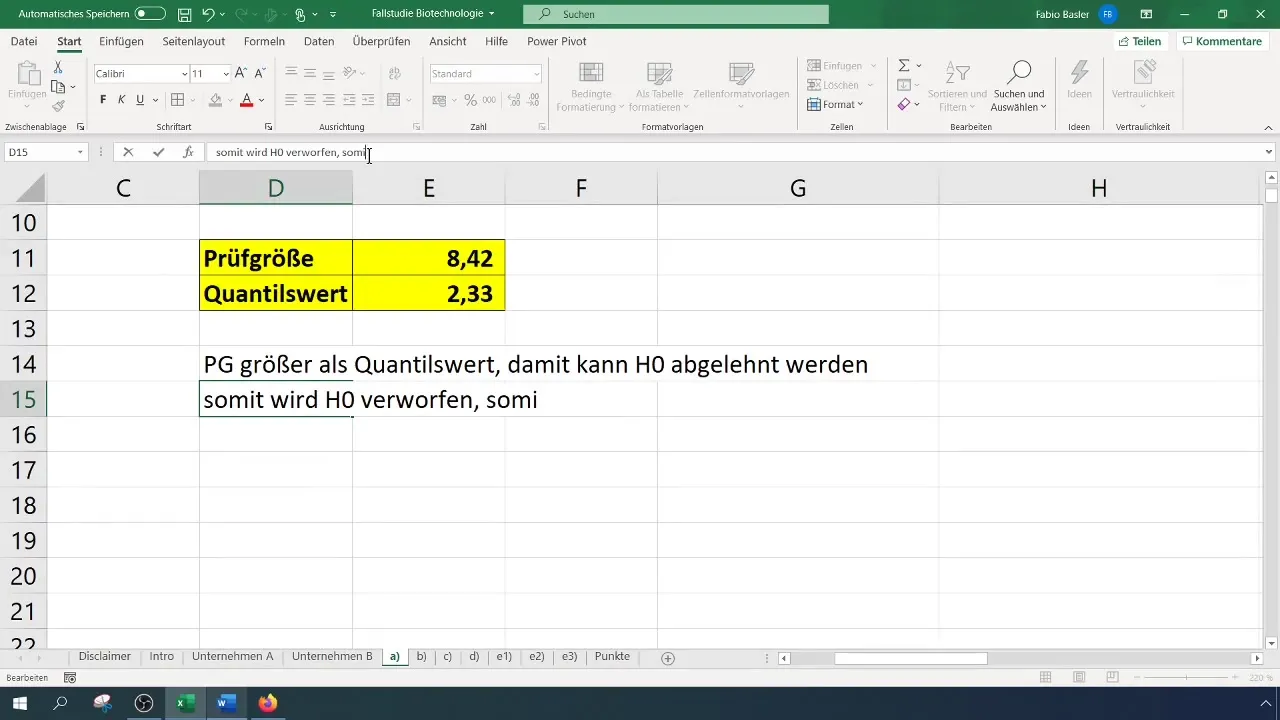
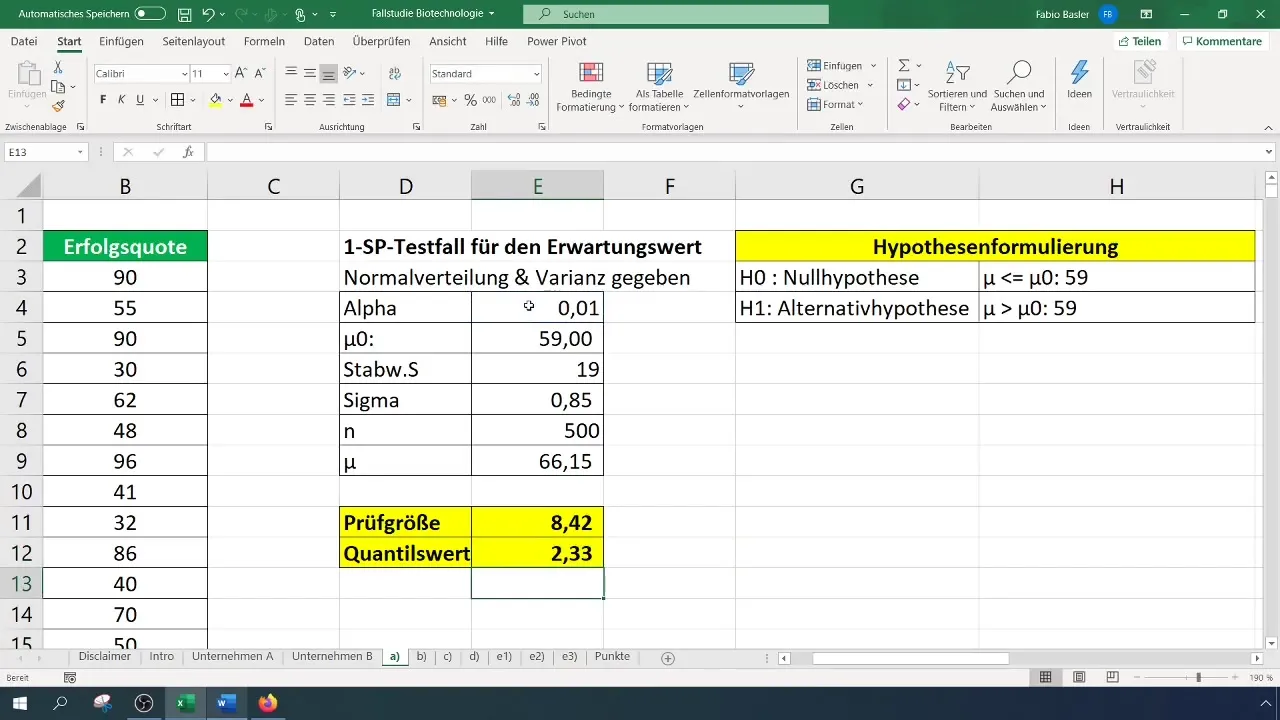
У нашому випадку значення критерію становить 8,4, що перевищує критичне значення 2,33. Отже, ми можемо відхилити нульову гіпотезу. Це свідчить про те, що частка успішності значно поліпшилася.
Інтерпретація результатів
Після того, як ви провели тест і визначили результати, вам слід чітко інтерпретувати їх в чіткому контексті. Відхилення нульової гіпотези означає, що перевірений новий показник значно відрізняється від минулого, у цьому випадку 59%.
Ця інформація має велике значення для стратегічного прийняття рішень у вашому підприємстві. Вона підтверджує, що зусилля з поліпшення показників успішності були успішними.
Загальний висновок
У цьому посібнику ви дізналися, як провести тест 1-SP для математичного очікування в Excel. Через кейс-стадію ви бачили кроки від формулювання гіпотези до обчислення даних і інтерпретації результатів. Ці знання не лише цінні для наукових досліджень, але й для практичних застосувань у підприємстві.


