Статистичні тести є невід'ємною частиною аналізу даних, особливо коли мова йде про перевірку відмінностей між групами. Перевірений метод, який часто використовується в дослідженнях і економіці, - це тест Ф для двох вибірок. Цей посібник покаже вам крок за кроком, як реалізувати таке тестування в Excel, щоб порівняти змінні двох фармацевтичних компаній щодо їхніх витрат на дослідження.
Основні висновки
- Ви дізнаєтеся, як порівнювати дисперсію двох груп за допомогою тесту Ф.
- Цей посібник містить детальні кроки щодо виконання тесту в Excel, включаючи використання функції аналізу даних.
- У кінці ви будете знати, як інтерпретувати результати та які висновки можна зробити.
Посібник крок за кроком
Крок 1: Підготовка даних
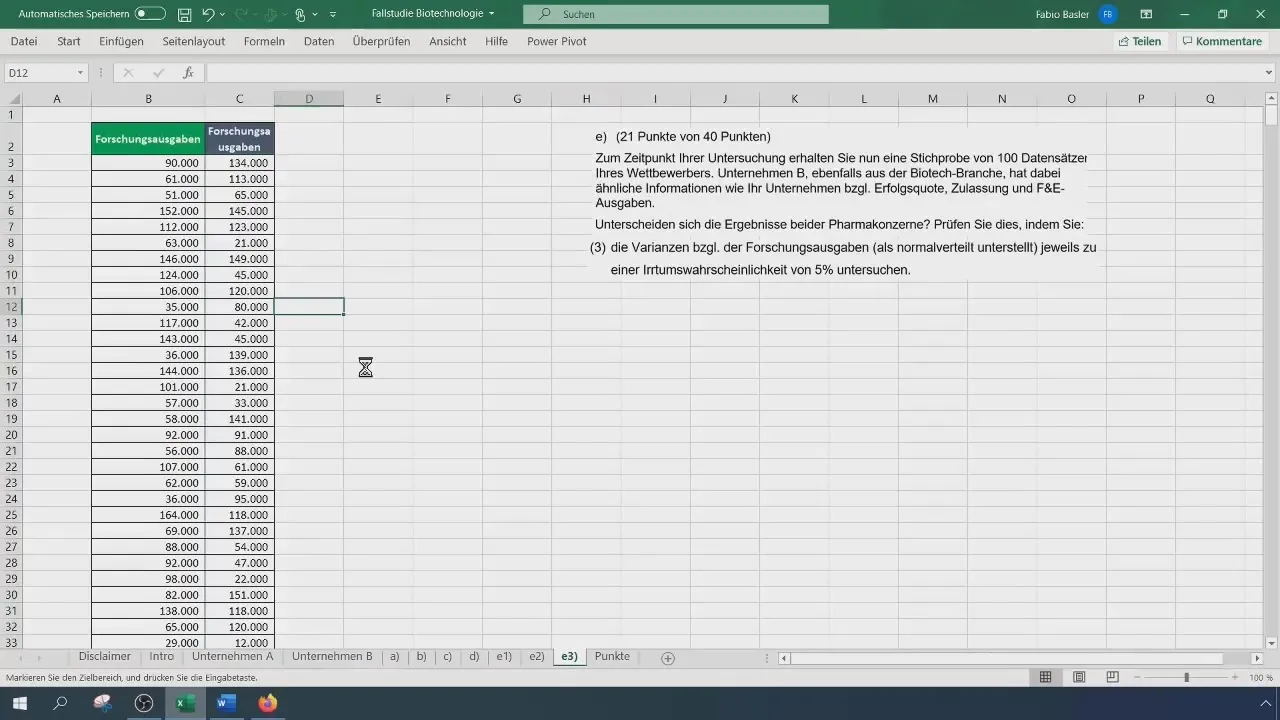
Спочатку вам знадобляться початкові дані щодо витрат на дослідження обох компаній. Відкрийте ваш файл Excel та скопіюйте дані про дослідження обох компаній в окремі стовпці.

Крок 2: Обсяг вибірки та розрахунок дисперсії
Розмір вашої вибірки залишається однаковим: 500 для компанії A та 100 для компанії B. Для розрахунку дисперсії використайте функцію VAR.S(), щоб оцінити дисперсію для груп. Обережно введіть значення у форматі Excel для отримання точних результатів.
Крок 3: Формулювання гіпотез
Для тесту Ф гіпотези формулюються наступним чином:
- Нульова гіпотеза (H0): σ1² = σ2² (Дисперсії двох компаній рівні).
- Альтернативна гіпотеза (H1): σ1² ≠ σ2² (Дисперсії двох компаній не рівні).
Крок 4: Розрахунок критерію
Розрахуйте критерій (статистика F) за допомогою відношення двох дисперсій. Використовуйте формулу Дисперсія_А / Дисперсія_В. Після введення дисперсій, ви отримаєте статистику F для порівняння.
Крок 5: Визначення критичного значення
Для визначення критичного значення F вам потрібен рівень альфа (зазвичай 0,05) та ступені свободи. Ступені свободи обчислюються так: df1 = n1 - 1 та df2 = n2 - 1. Розрахуйте критичне значення за допомогою функції F.INV().

Крок 6: Прийняття рішення
Порівняйте розраховану статистику F з критичним значенням F. Якщо статистика F більше за критичне значення, відхиліть нульову гіпотезу, в іншому випадку ні. У цьому прикладі критерієм для відхилення є те, що статистика повинна бути меншою за критичне значення (F критичне).

Крок 7: Використання функції аналізу даних в Excel
У Excel є можливість також виконати тест Ф за допомогою функції аналізу даних. Перейдіть в "Дані" і виберіть "Аналіз даних". Оберіть "Тест Ф для двох вибірок". Введіть діапазони для обох змінних і виберіть відповідні налаштування.
Крок 8: Інтерпретація результатів
Аналізуйте результати тесту Ф. Якщо розрахована статистика F та p-значення у виведенні Excel демонструють ті ж результати, що і ваші ручні розрахунки, можна зробити висновок, що дисперсії двох компаній однакові.
Підсумок
Тест Ф для двох вибірок є необхідним інструментом в статистичному аналізі, який дозволяє порівнювати відмінності в дисперсії між двома групами. У цьому посібнику ви навчились ефективно виконувати цей тест в Excel, від підготовки даних до інтерпретації результатів.
Часті запитання
Що таке тест Ф для двох вибірок?Тест Ф для двох вибірок порівнює дисперсії двох груп, щоб визначити, чи вони статистично значуще відрізняються.
Коли слід використовувати тест Ф?Тест Ф використовується, коли ви хочете перевірити одність дисперсій у двох незалежних групах.
Як розрахувати статистику F?Статистика F розраховується, ділячи дисперсію першої групи на дисперсію другої групи.
Що робити, якщо нульову гіпотезу відхиляють?Якщо нульову гіпотезу відхиляють, можна припустити, що дисперсії двох груп статистично значуще відрізняються.
Чи є альтернативи тесту Ф?Так, ви можете використовувати також тест Бартлетта або тест Лівена, якщо ви хочете перевірити однорідність дисперсії.


