Критерій адаптації χ² відображає простий метод перевірки гіпотези про те, чи послідовність даних відповідає нормальному розподілу. У цьому посібнику ви навчитесь, як виконати тест χ² в Excel, щоб визначити, чи обороти смартфонів відповідають нормальному розподілу. Ми пройдемо крок за кроком через процес, що починається з створення класифікованої таблиці частот та закінчується розрахунком випробувальної величини й порівнянням з критичним значенням χ².
Основні висновки
- Тест адаптації χ² допомагає в перевірці нормальних розподілів.
- Важливо створити класифіковану таблицю частот.
- Випробувальну величину порівнюють з критичним значенням, щоб відхилити або прийняти нульову гіпотезу.
Посібник по кроках
Крок 1: Підготовка даних
Для виконання тесту χ² спочатку потрібні дані. Скопіюйте обороти смартфонів в Excel-таблицю. Переконайтеся, що ваші дані організовані в одному стовпці.

Крок 2: Створення гістограми
Щоб отримати перші візуальні вказівки щодо розподілу, створіть гістограму ваших даних. Перейдіть у вкладку "Вставка" та виберіть "Діаграми". Додайте гістограму, вибравши діапазон даних.
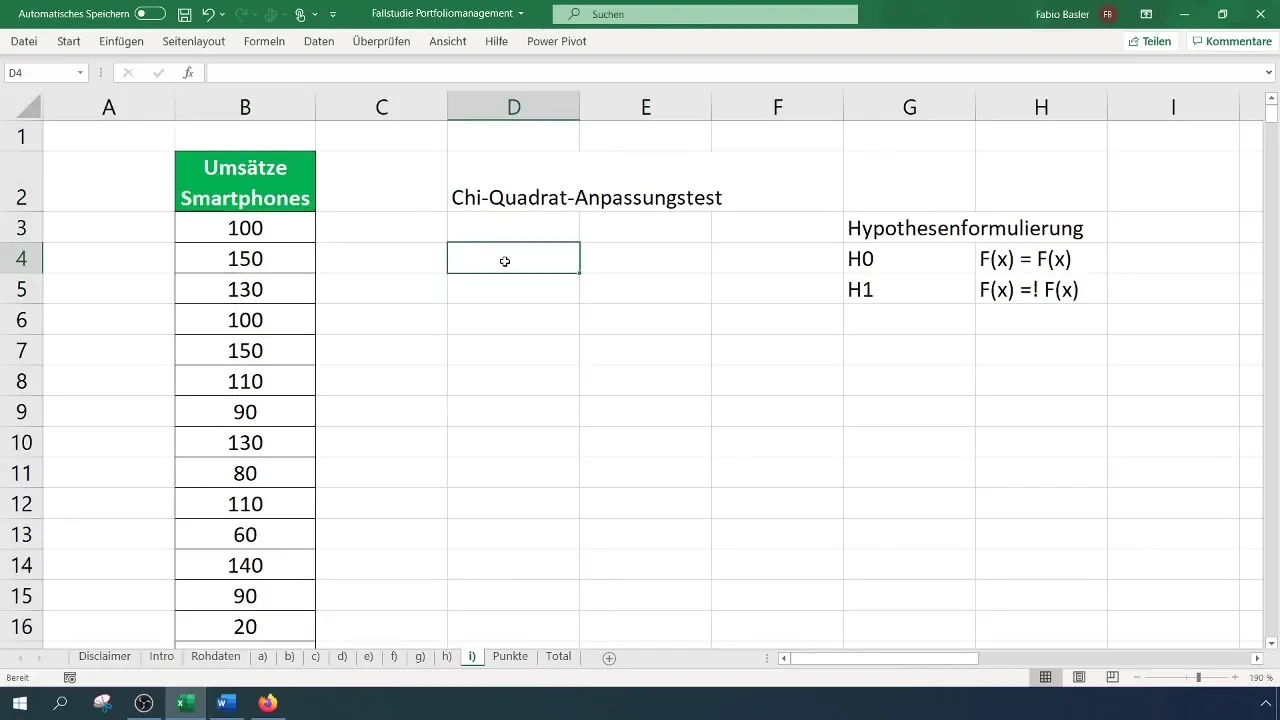
Крок 3: Створення класифікованої таблиці частот
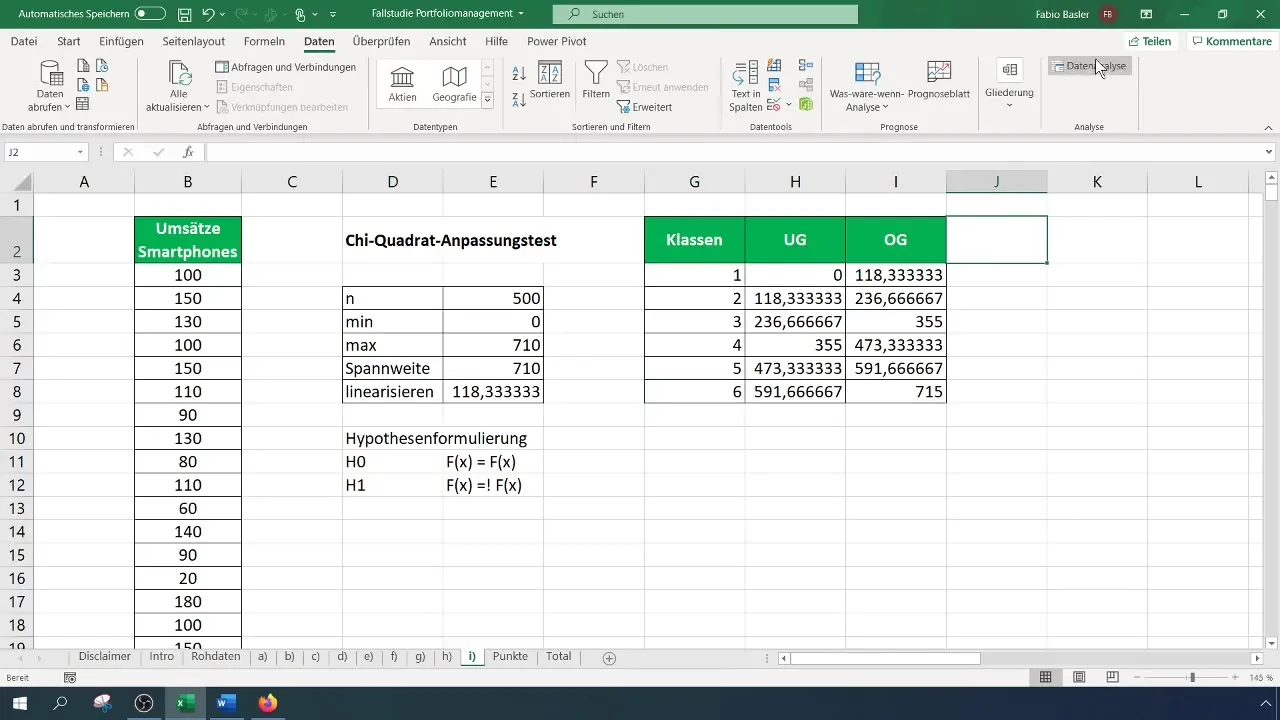
Для тесту χ² потрібна класифікована таблиця частот. Спочатку визначте кількість класів для своєї таблиці – у цьому випадку ми використовуємо шість класів. Розрахуйте ширину інтервалів та створіть таблицю відповідно.
Крок 4: Розрахунок частот
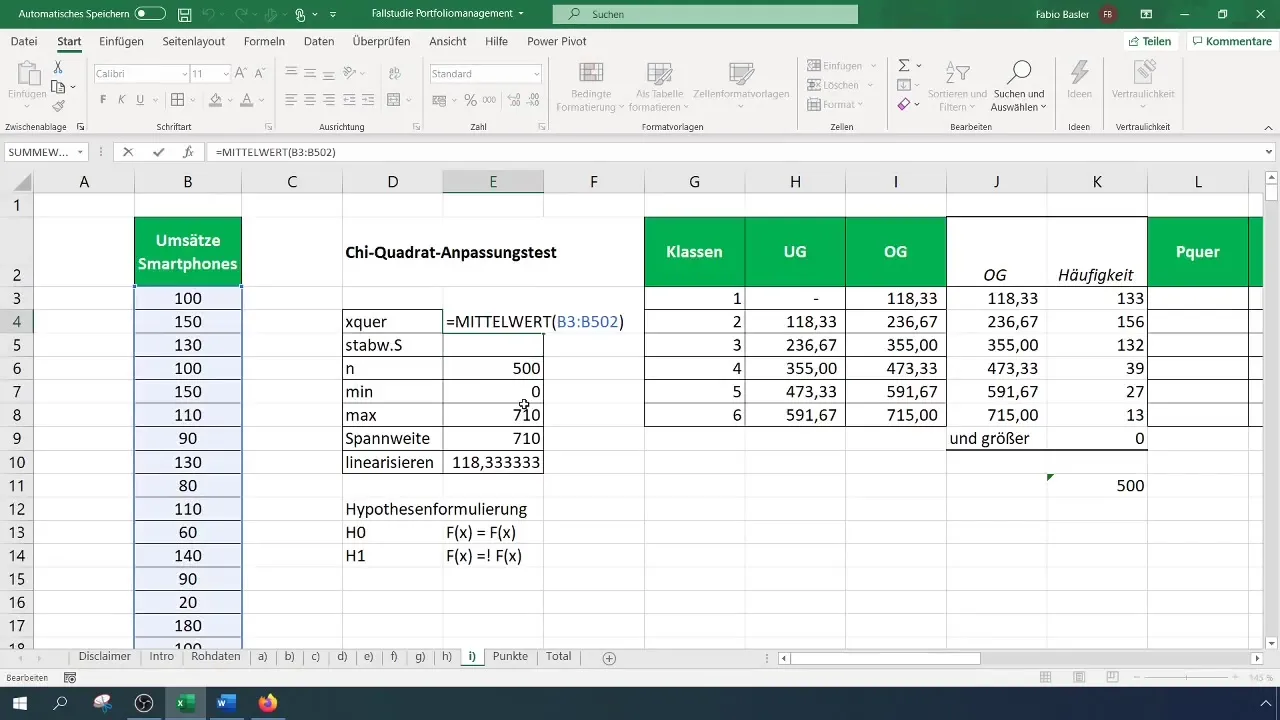
Тепер вам потрібно розрахувати спостережувані частоти для кожного класу. Перейдіть у меню вкладки "Аналіз даних" та виберіть "Гістограма". Оберіть діапазон вхідних даних та межі класів. Визначте діапазон вихідних даних для таблиці частот.
Крок 5: Розрахунок очікуваних частот
Для визначення очікуваних частот розрахуйте ймовірності для кожного класу на основі припущеного нормального розподілу. Для цього вам знадобиться середнє значення та стандартне відхилення ваших даних.
Крок 6: Розрахунок випробувальної величини
Розрахуйте випробувальну величину (χ²) за формулою:
[ χ^2 = ∑(O_i - E_i)^2 / E_i ]
де (O_i) - спостережувані, а (E_i) - очікувані частоти. Ви можете здійснити цей розрахунок в Excel, зберігши кожну компоненту в окремих клітинках.
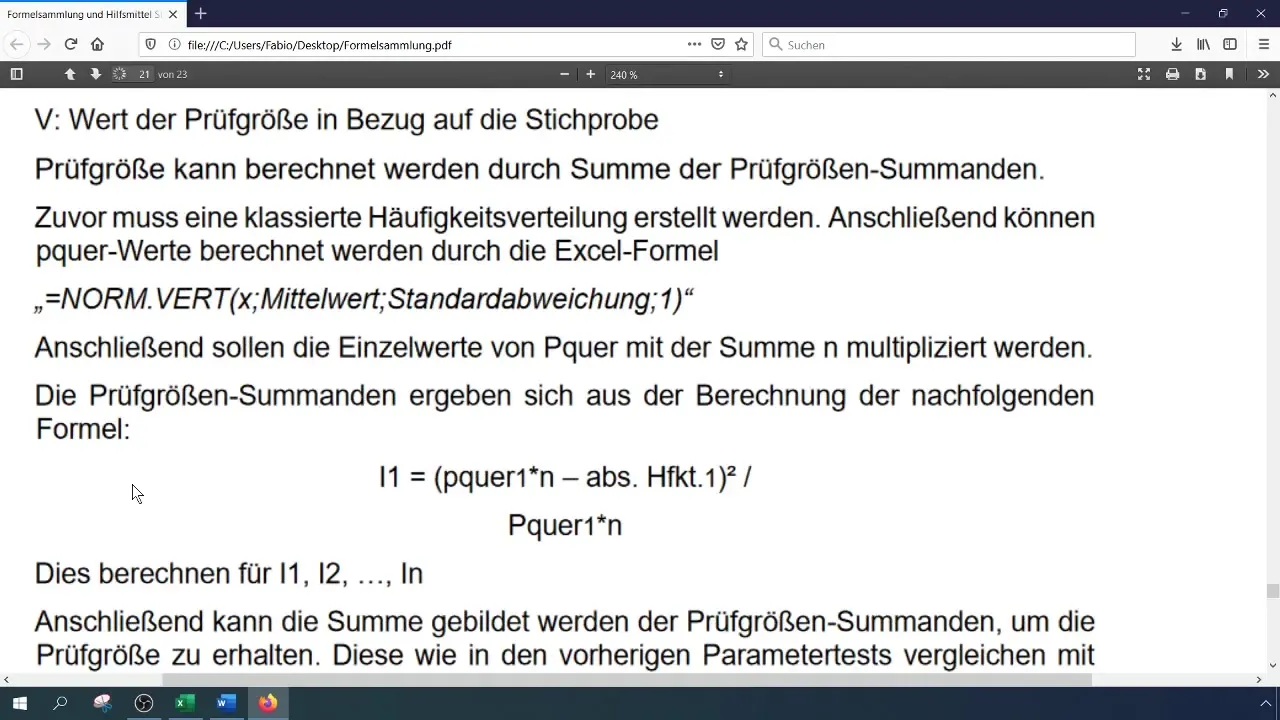
Крок 7: Розрахунок критичного значення
Для оцінки випробувальної величини вам потрібно розрахувати критичне значення (χ²) для вашого довірчого рівня та кількості ступенів свободи. Кількість ступенів свободи для тесту χ² дорівнює (k - 1), де (k) - кількість класів.
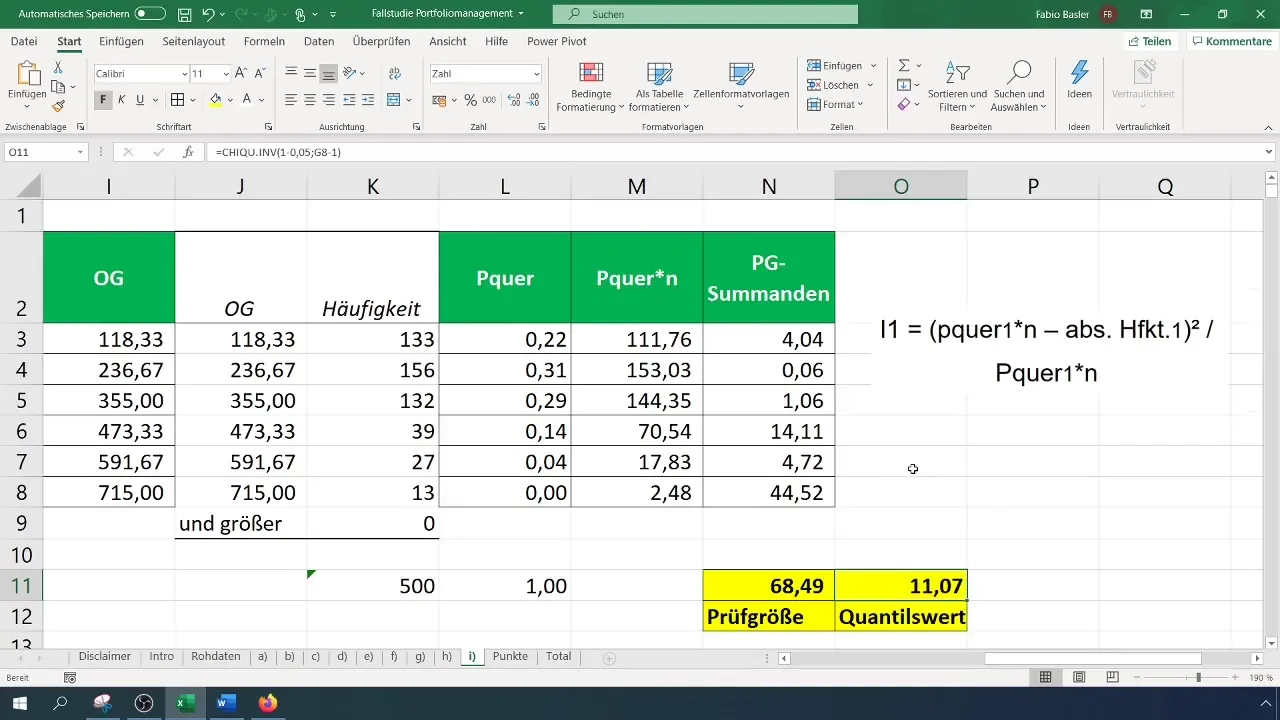
Крок 8: Перевірка гіпотез
Порівняйте розраховану випробувальну величину з критичним значенням. Якщо випробувальна величина більша за критичне значення, відхиліть нульову гіпотезу, що означає, що дані не мають нормального розподілу. В іншому випадку прийміть нульову гіпотезу.
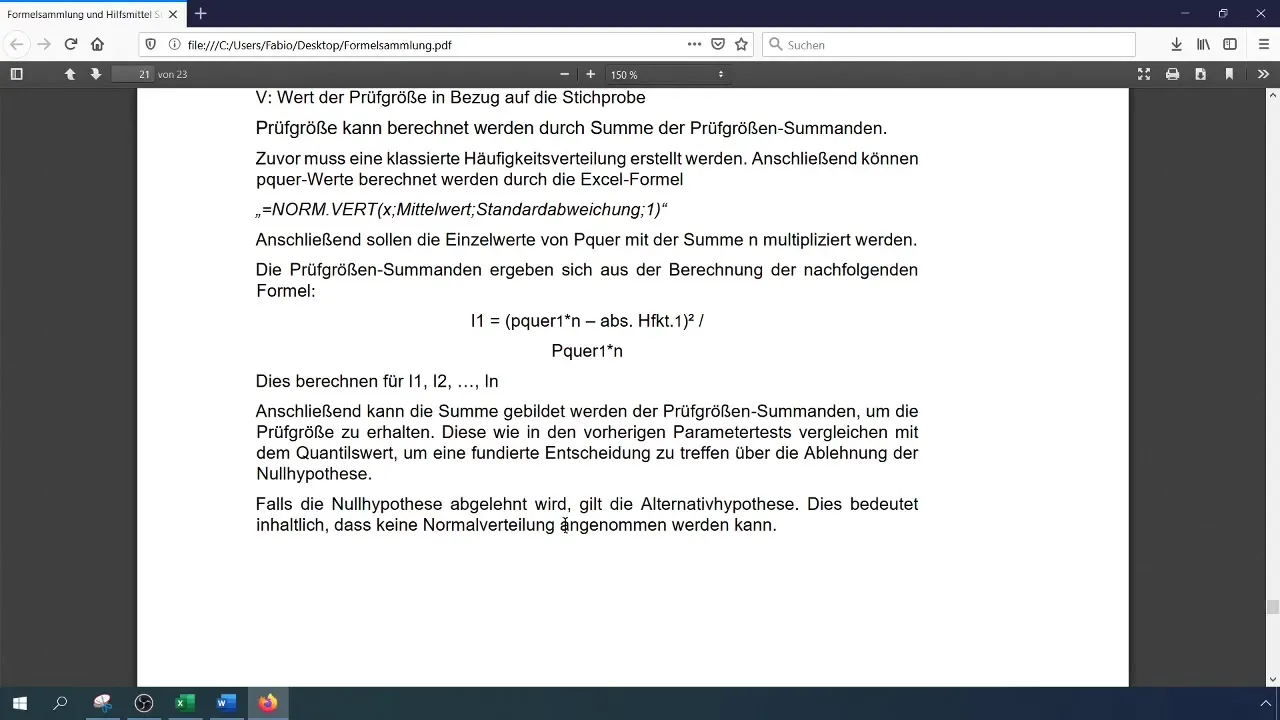
Крок 9: Підведення підсумків
Зафіксуйте свої результати та розширте їх графічними даними та гіпотезними тестами. Не забувайте перевірити свою гістограму, щоб візуально підтвердити, що розподіл не є нормальним.
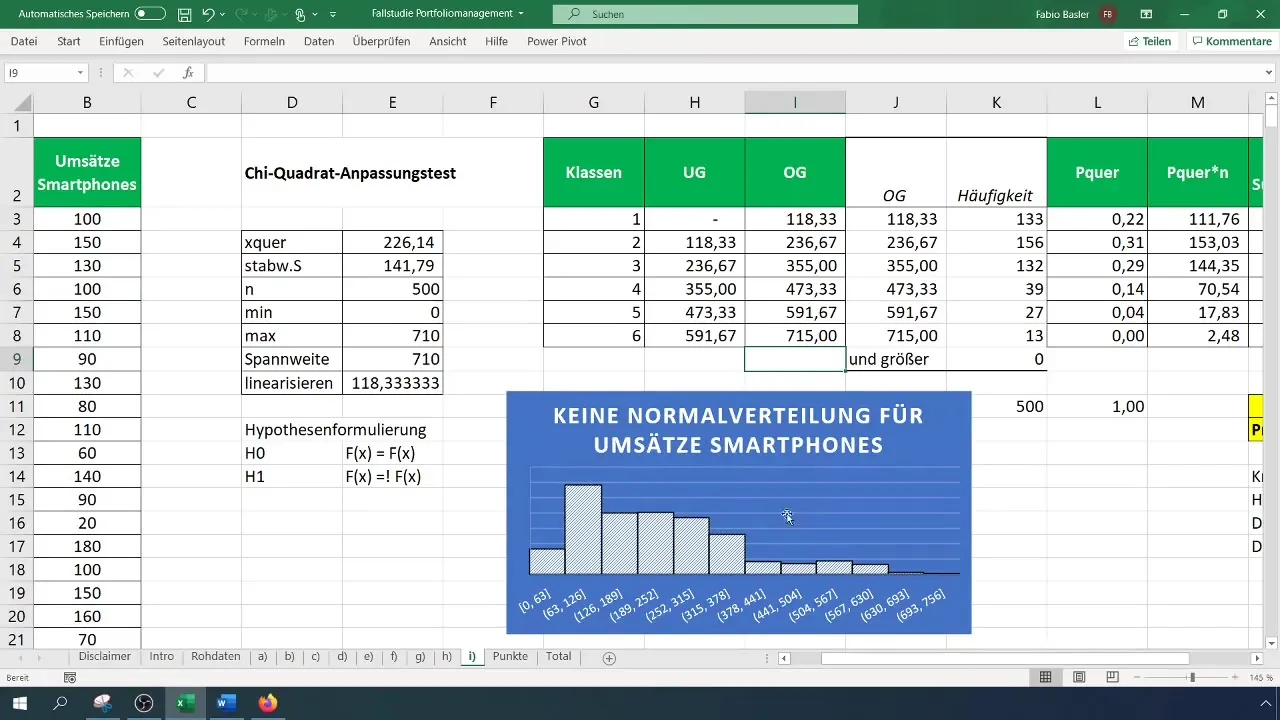
Підсумок
Протягом цього керівництва ви навчились, як проводити тест адаптації хі-квадрат в Excel, щоб проаналізувати нормальний розподіл доходів від смартфонів. Кроки включають створення таблиці частот, обчислення очікуваних частот, статистики тесту та, нарешті, порівняння з критичним значенням.
Часто задані питання
Що таке тест адаптації хі-квадрат?Тест адаптації хі-квадрат перевіряє, чи відповідає спостережена частотна розподіл гаусовському розподілу.
Скільки класів потрібно для таблиці частот?Зазвичай рекомендується мати принаймні від 5 до 10 класів для аналізу даних.
Що робити, якщо нульова гіпотеза відхиляється?Якщо ви відкидаєте нульову гіпотезу, це означає, що дані не мають нормального розподілу.
Як обчислити критичне значення хі-квадрат?Критичне значення вираховується на основі ступенів свободи та бажаного рівня значущості з таблиці розподілу хі-квадрат.


