Статистичні аналізи є невід’ємним інструментом у портфельному управлінні. Особливо потужним методом є регресійний аналіз, особливо коли йдеться про визначення впливу кількох незалежних змінних на залежну змінну. Хочеш дізнатися, як у програмі Excel побудувати та проаналізувати лінійний функціональний зв'язок за допомогою множинної регресії? Цей посібник надасть тобі чіткий огляд та детальну посібник по кроку.
Найважливіші висновки
- Регресійний аналіз допомагає кількісно оцінити вплив незалежних змінних на залежну змінну.
- Важливо оцінити якість і статистичну значимість регресійної моделі.
- Оцінюючи коефіцієнти, можна визначити, яка незалежна змінна має сильніший вплив на залежну змінну.
Посібник по кроку на регресійний аналіз в Excel
Підготовка даних
Перш ніж розпочати регресійний аналіз, потрібно підготувати дані. Залежна змінна (y) у цьому випадку - обіг ноутбуків, а незалежні змінні (x1 та x2) - кількість працівників та кількість акцій конкурентів. Спочатку введіть всі необхідні дані в Excel та структуруйте їх зручно.
Перевірка кореляції
Щоб отримати перші вказівки щодо можливих зв'язків між змінними, можна створити кореляційну матрицю. Ця матриця допоможе вам побачити, наскільки сильно різні змінні пов'язані між собою. Це можна зробити за допомогою функції "Аналіз даних" в Excel, вибравши потім кореляційну матрицю та включивши всі відповідні діапазони даних.
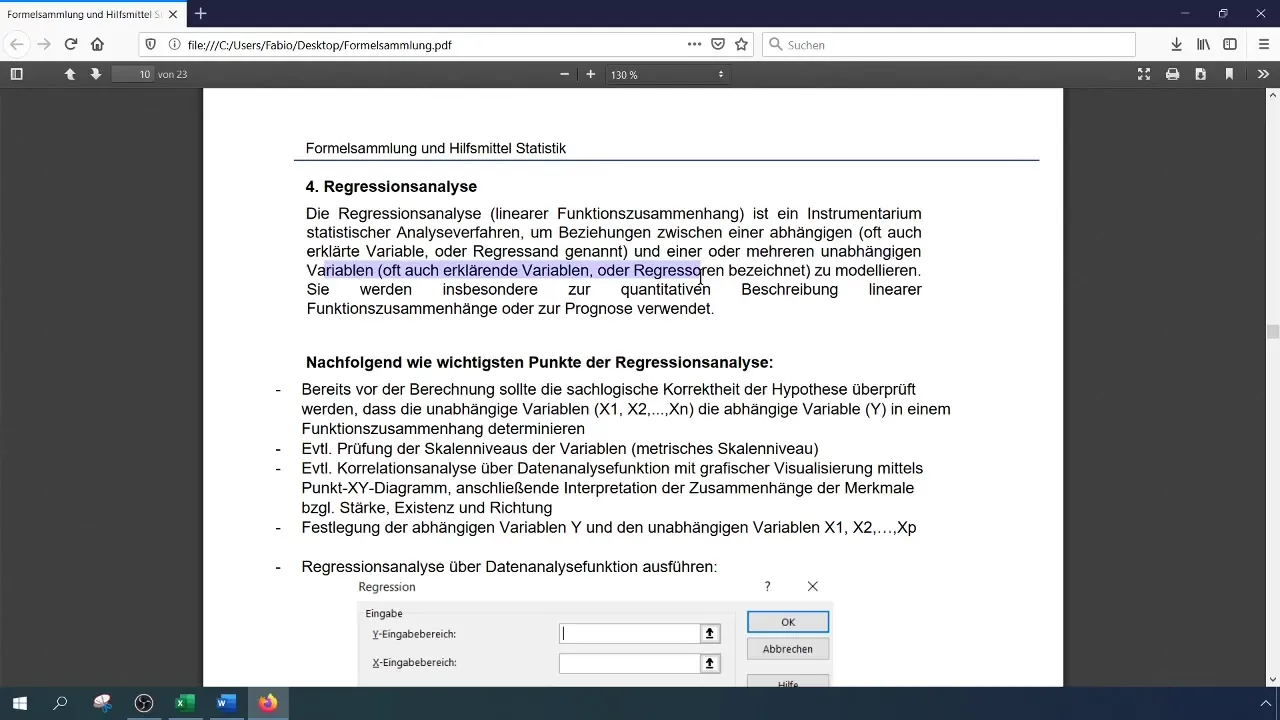
Проведення регресійного аналізу
Зараз ви готові виконати регресійний аналіз. Для цього знову виберіть функцію "Аналіз даних", потім виберіть "Регресія". Тут ви вказуєте діапазон для залежної змінної (обіг ноутбуків) та незалежних змінних (кількість працівників та акції конкурентів).
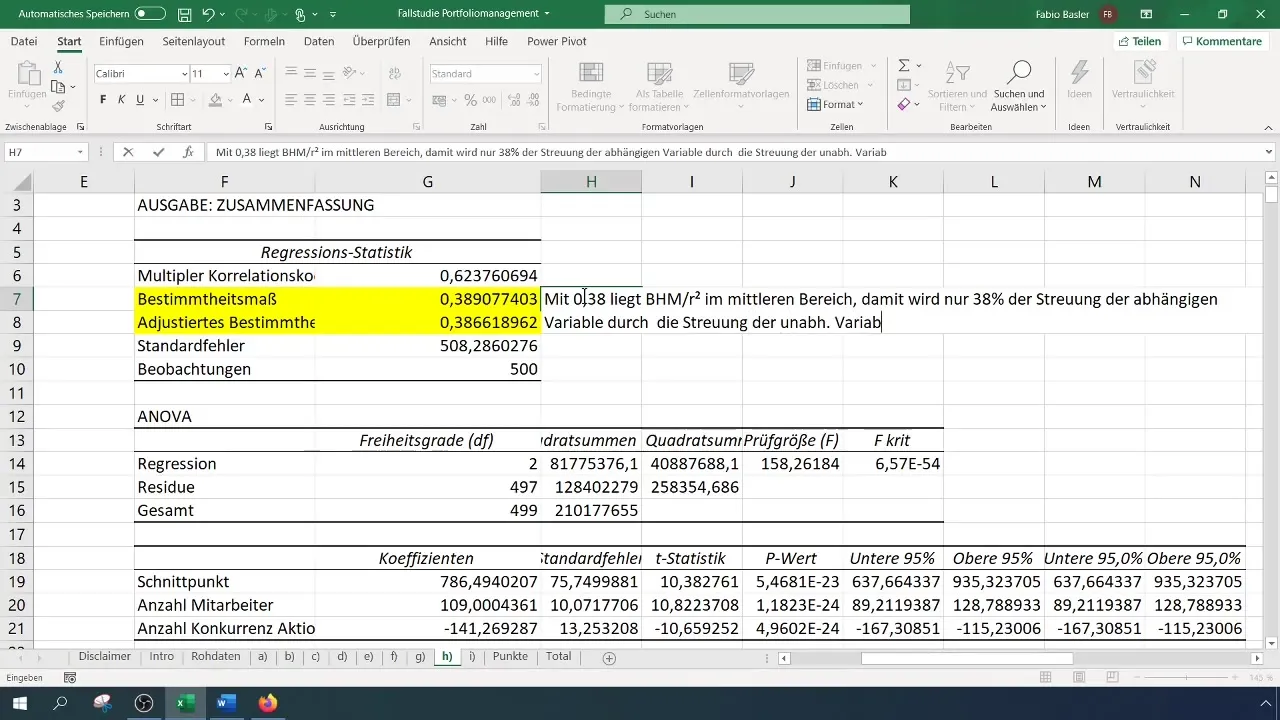
Інтерпретація результатів
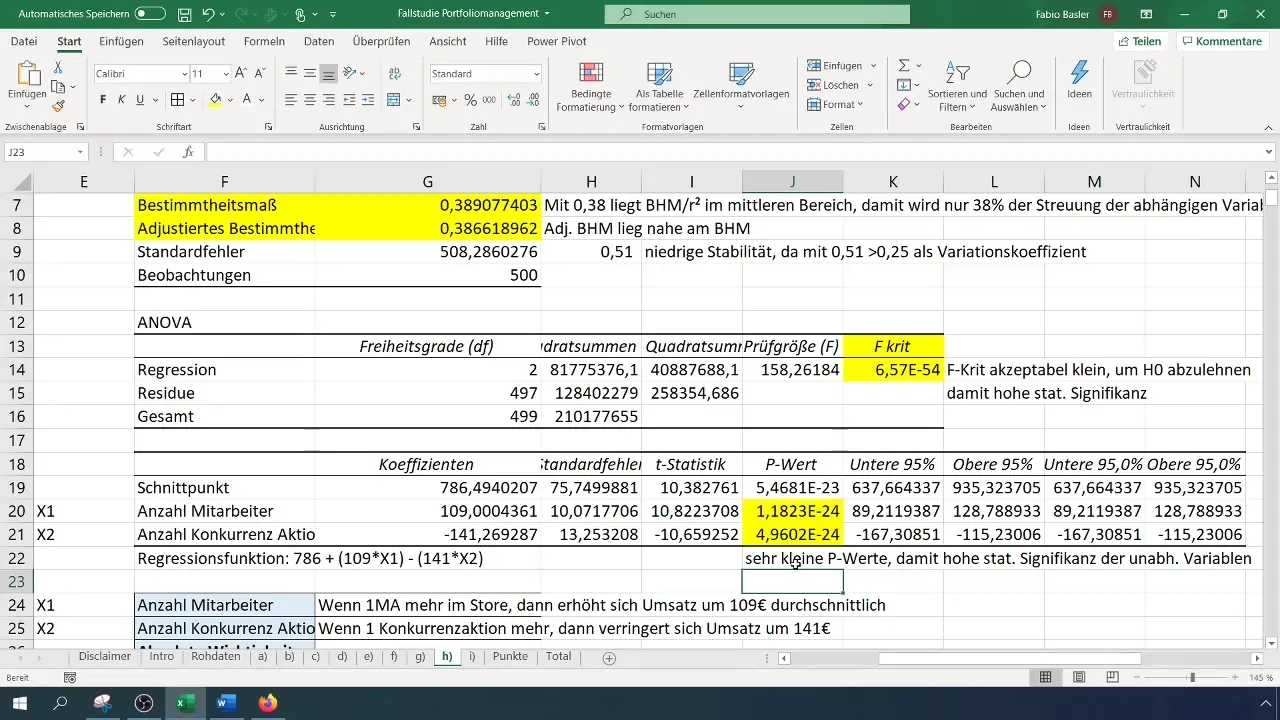
Після проведення регресійного аналізу ви отримаєте багато виведених даних і статистики. Перша важлива точка - це коефіцієнт детермінації (R²), який описує частку пояснення залежної змінної незалежними змінними. Значення R² рівне 0,38 вказує на те, що 38% змінливості в обороті можна пояснити цими двома незалежними змінними.
Під час аналізу варто звернути увагу на стабільність моделі. Тут ви можете використати стандартну помилку для визначення стабільності. Наприклад, якщо ви отримаєте стандартну помилку 0,51, це означає велику відносну коливання та низьку стабільність.
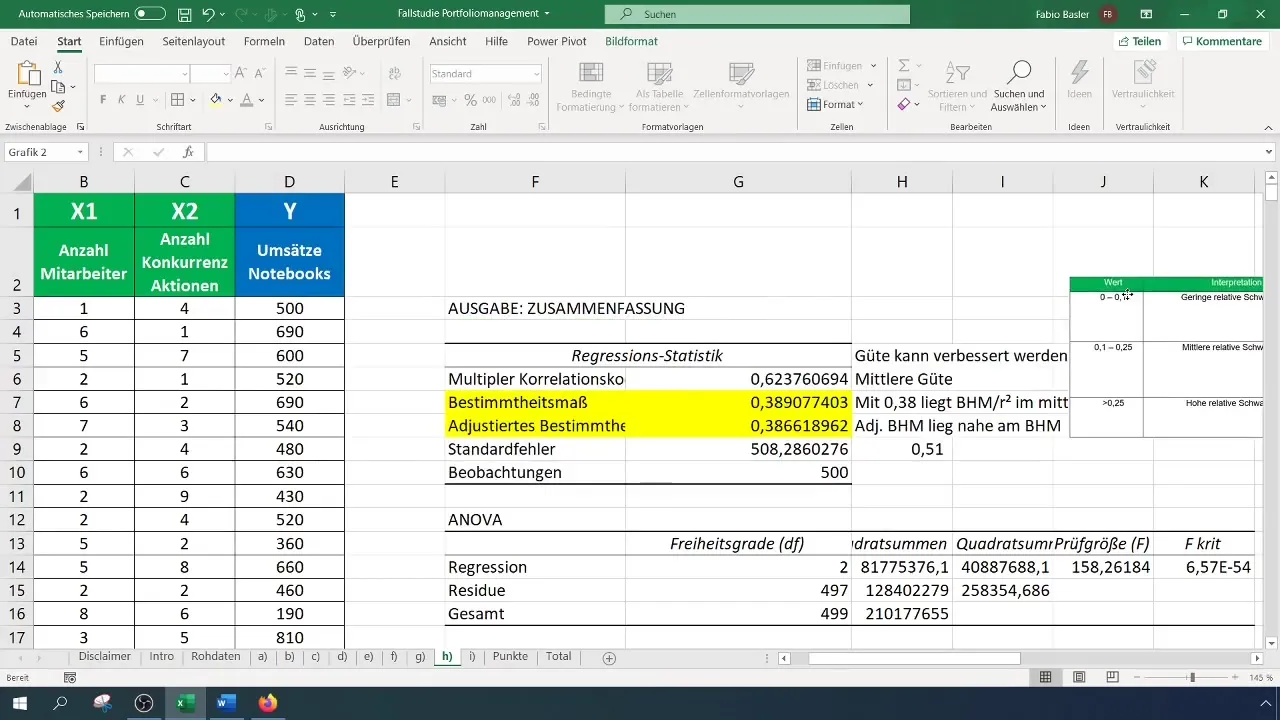
Оцінка сильних факторів впливу
Рішучим кроком є з'ясування, яка з незалежних змінних має сильніший вплив на залежну змінну. Це можна зробити за допомогою коефіцієнтів, які вказують абсолютне значення змінних. Так от, коефіцієнт x1 (кількість працівників) дорівнює 109, тоді як коефіцієнт x2 (кількість акцій конкурентів) дорівнює -141. Це вказує на те, що кожне збільшення кількості працівників збільшує оборот на 109 євро, тоді як кожне збільшення акцій конкурентів зменшує оборот на 141 євро.
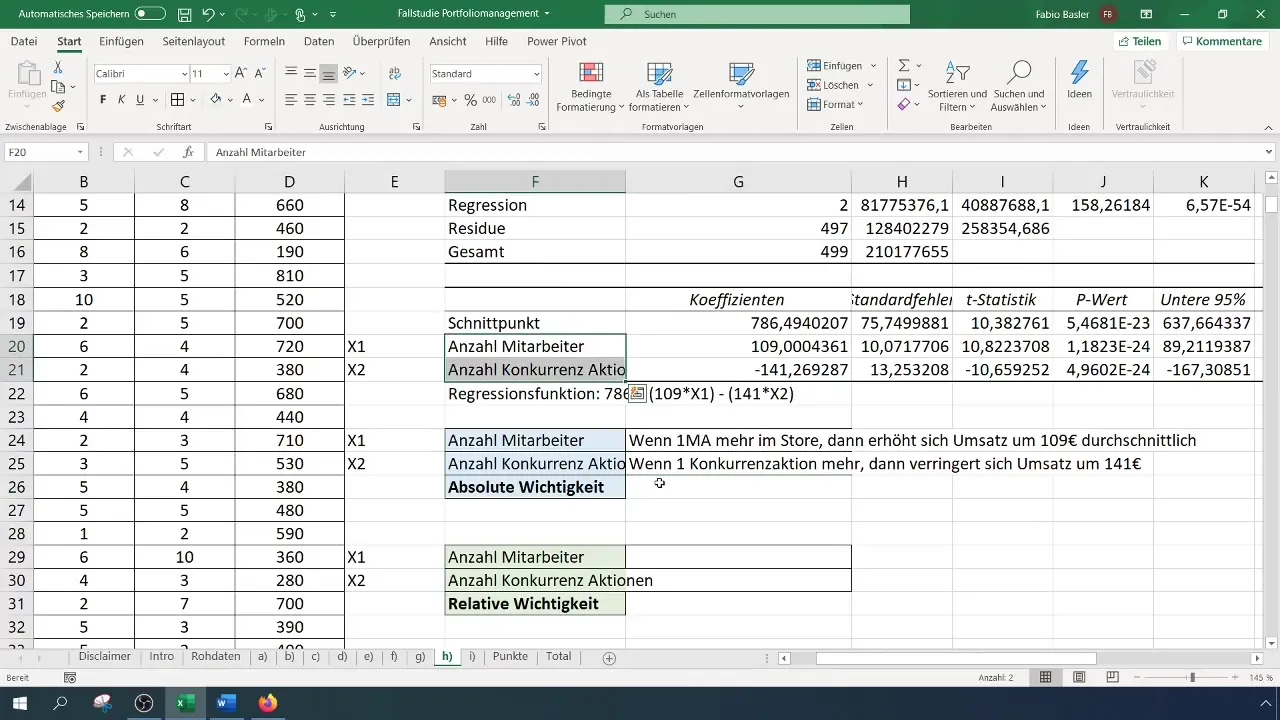
Оцінка статистичної значимості
Ще одним важливим аспектом регресійного аналізу є статистична значимість. Це можна відчитати з p-значень та F-тесту, які повинні мати дуже малі значення. Це показує, що незалежні змінні мають значний вплив на залежну змінну, що виправдовує використання моделі.
Підсумок
Регресійний аналіз в Excel дозволяє вам кількісно оцінити зв'язок між різними змінними. Завдяки цьому посібнику ви дізналися про кроки для виконання та інтерпретації множинної регресії. Пам'ятайте критично оцінювати якість і стабільність моделі, а також окремі фактори впливу для прийняття обґрунтованих рішень у портфельному управлінні.
Часто задовані питання
Які дані мені потрібні для регресійного аналізу?Вам потрібна залежна змінна (наприклад, оборот) і принаймні одна або кілька незалежних змінних (наприклад, кількість працівників, конкурентні акції).
Як інтерпретувати показник R²?Вище значення R² означає, що більша частина змінності залежної змінної пояснюється незалежними змінними.
Як перевірити статистичну значимість?Ви можете використовувати p-значення і F-тест; низькі значення вказують на високу значимість.
В чому різниця між R² та скоригованим R²?Скоригований R² враховує кількість незалежних змінних і надає більш реалістичну оцінку в моделях з декількома змінними.
Як оцінити силу факторів впливу?Це відбувається за допомогою розглядання коефіцієнтів незалежних змінних, що кількісно характеризують вплив кожної змінної на залежну змінну.


