Аналіз рангової кореляції має центральне значення в статистичному аналізі взаємозв'язків між змінними. Особливо, коли мова йде про порядкові масштабовані дані, рангова кореляція Спірмена є цінним методом для розпізнавання закономірностей і зв'язків. У цьому покроковому посібнику ви дізнаєтеся, як розрахувати рангову кореляцію Спірмена для опитування за допомогою Excel.
Основні висновки
- Рангова кореляція вимірює силу і напрямок монотонного зв'язку між двома порядковими змінними.
- Коефіцієнт рангової кореляції Спірмена особливо корисний, коли одна зі змінних є порядковою, а інша - метричною.
- Його можна розрахувати в Excel за допомогою простих формул і функцій.
Покрокова інструкція
Спочатку ми визначаємо змінні, які хочемо проаналізувати. В даному випадку це задоволеність клієнтів (порядкова шкала, значення 1-3) та кількість замовлень (метрична шкала).
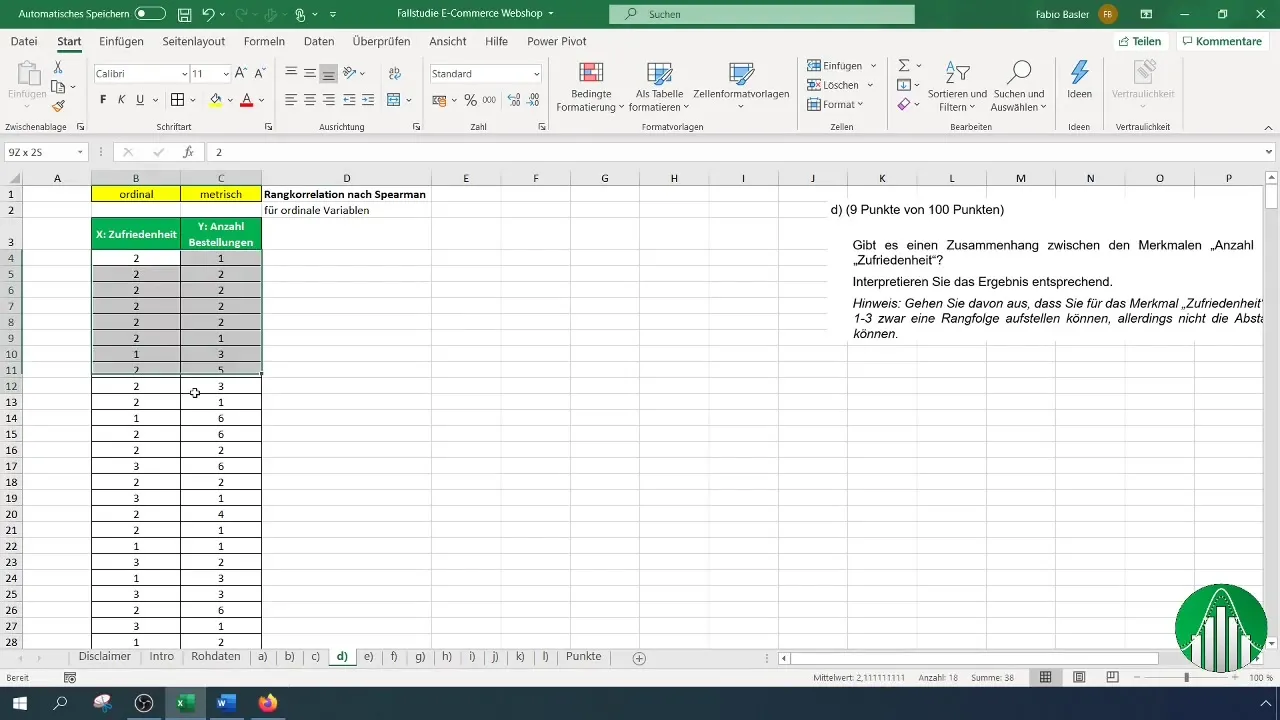
Щоб створити рейтинг за задоволеністю та кількістю замовлень, вам потрібна таблиця, що містить відповідні дані. Переконайтеся, що ви ввели ці дані в Excel.

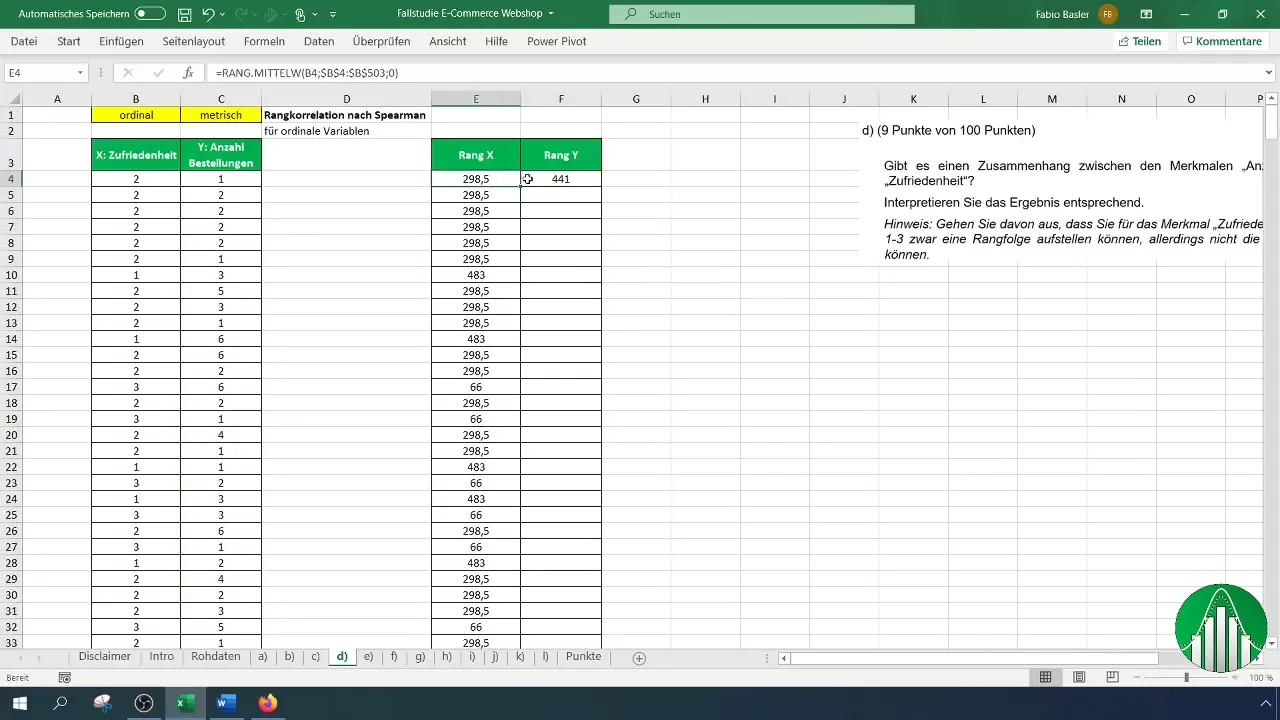
Після того, як ви ввели дані в Excel, давайте розглянемо розрахунок рангової кореляції за Спірменом. Для цього ми скористаємося функцією "Ранг.среднее" в Excel, яка повертає ранг числа в списку. Спочатку ми використовуємо формулу для задоволення:
Застосовуючи цю формулу, не забудьте вибрати стовпчик задоволеності і вказати весь діапазон від B4 до кінця вашого ряду даних, щоб правильно визначити ранги.
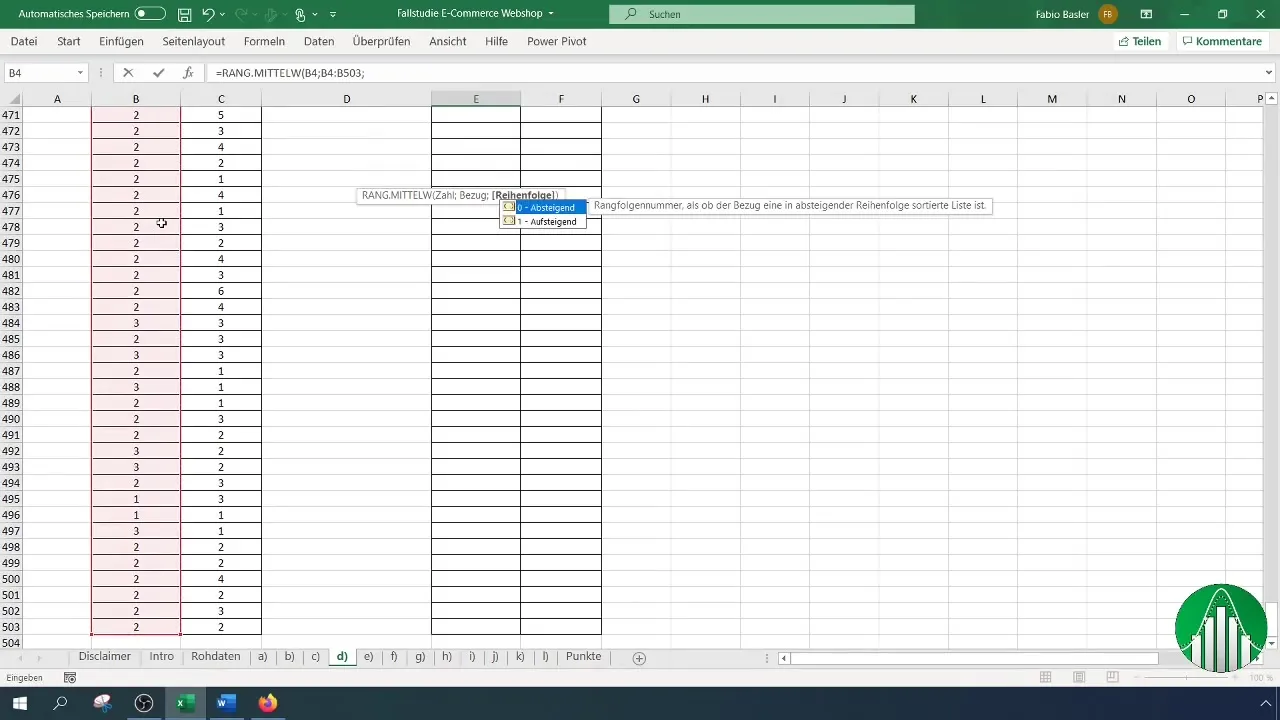
Вирішіть, чи хочете ви сортувати ранги за зростанням або за спаданням. Як правило, має сенс сортувати за зростанням. Зверніть увагу, що посилання на клітинки для рангів фіксуються за допомогою клавіші F4. Це важливо для того, щоб посилання не змінювалися під час копіювання.
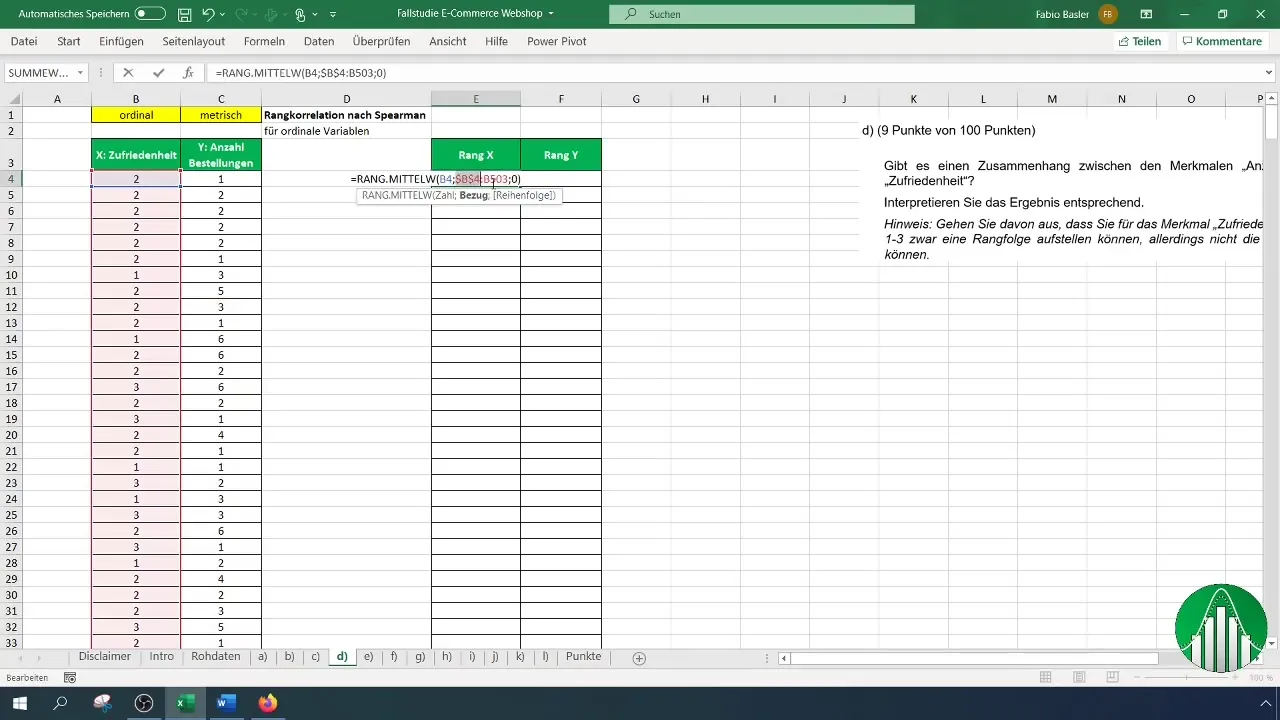
Після того, як ви встановили ранги для задоволеності, повторіть процес для кількості замовлень. Переконайтеся, що ви правильно застосували формулу і посилання.
Маючи обидва рейтинги (задоволеності та кількості замовлень), ви готові розрахувати коефіцієнт рангової кореляції Спірмена. Для цього використовуйте формулу "=КОРРЕЛ" для визначення зв'язку. Синтаксис наступний:
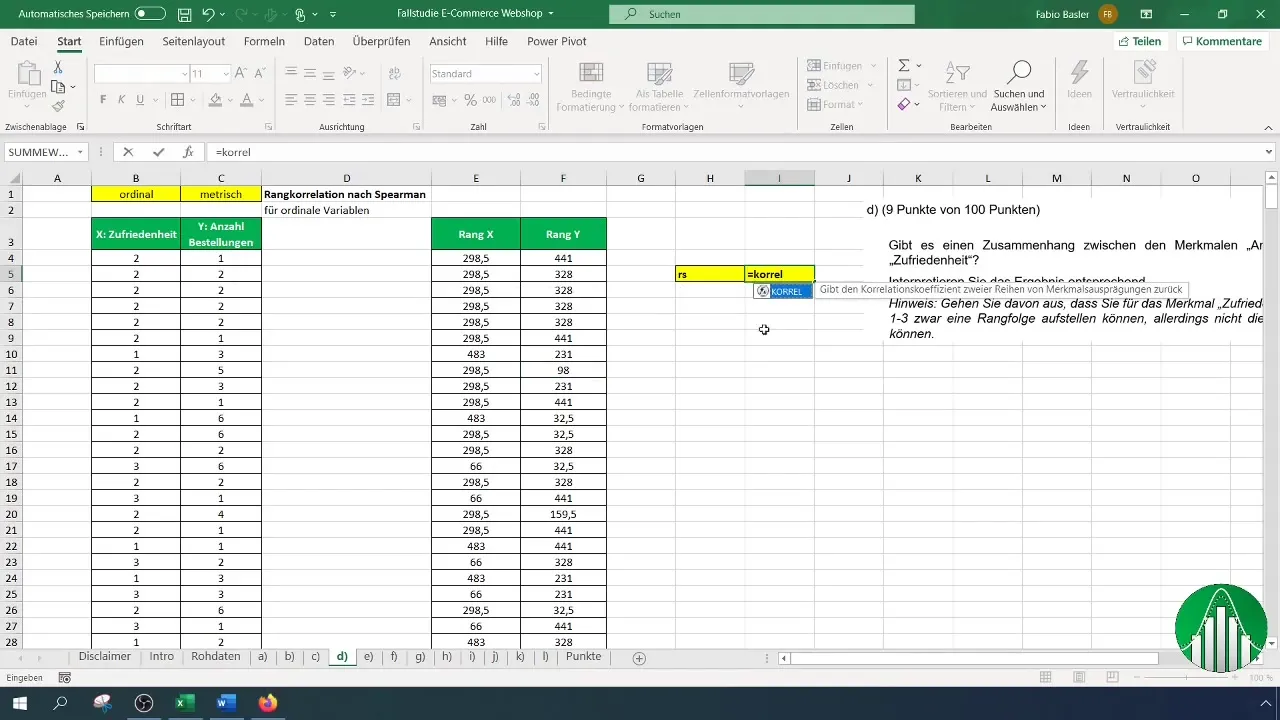
Введіть рейтинговий список задоволеності для першого посилання і рейтинговий список замовлень для другого. Тепер Excel автоматично розрахує коефіцієнт рангової кореляції Спірмена.

Який результат ви отримаєте? Значення 5,61% вказує на слабку позитивну кореляцію між задоволеністю і кількістю замовлень. Це означає, що між цими двома змінними навряд чи існує суттєвий зв'язок.
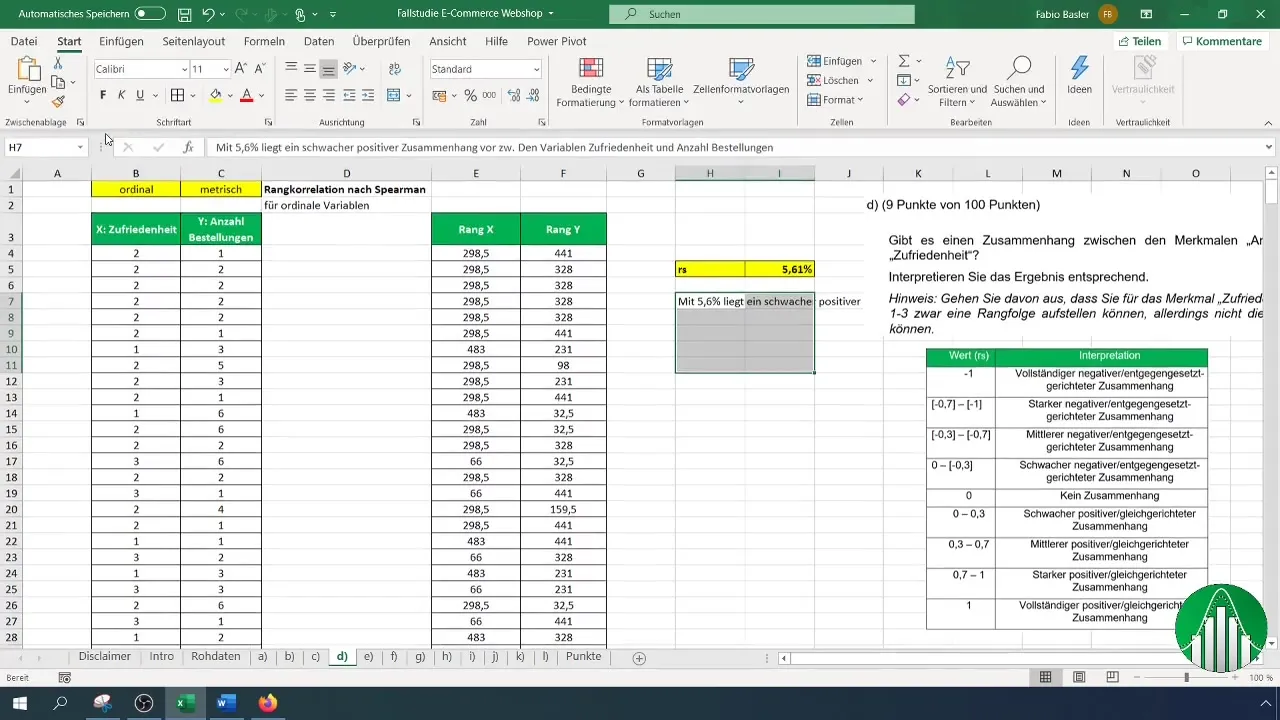
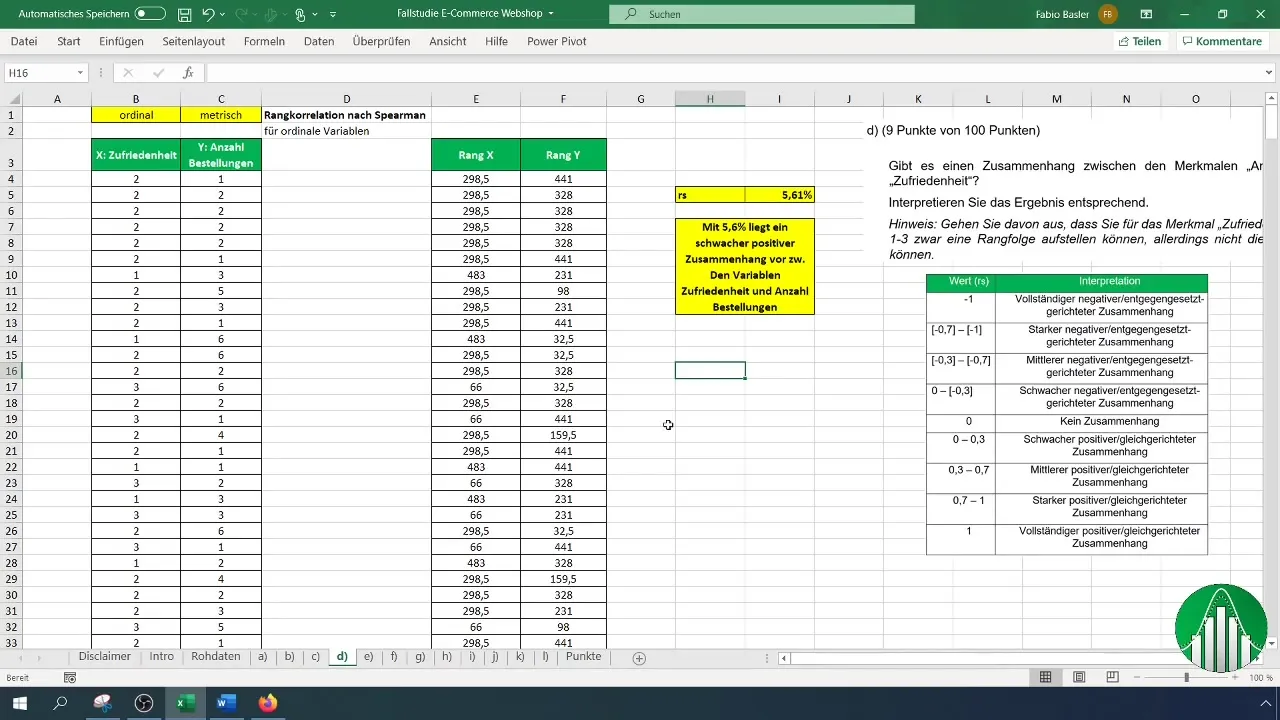
Для інтерпретації результатів використовуйте таблицю значень, що показує різні області рангової кореляції. Після інтерпретації ми підтверджуємо, що низький рівень кореляції означає, що змінні є відносно незалежними.
Підсумок
Виконання аналізу рангової кореляції Спірмена в Excel дозволяє отримати цінну інформацію про взаємозв'язки між порядковими та метричними змінними. Метод простий у використанні і дає чітке уявлення про будь-які кореляції.
Найпоширеніші запитання
Що таке коефіцієнт рангової кореляції Спірмена? Коефіцієнт рангової кореляції Спірмена вимірює силу і напрямок монотонного зв'язку між двома змінними.
Коли корисно використовувати коефіцієнт Спірмена? Він корисний, коли принаймні одна зі змінних є звичайним масштабуванням.
Як розрахувати коефіцієнт Спірмена в Excel?використовуйте функцію "ранг.среднее" для визначення рангів, а потім функцію "КОРРЕЛ" для розрахунку зв'язку.
Який діапазон значень коефіцієнта Спірмена? Коефіцієнт знаходиться в межах від -1 до 1. Значення, близькі до 1, вказують на сильну позитивну кореляцію, тоді як значення, близькі до -1, вказують на сильну негативну кореляцію.
Що може означати значення 5,61% для рангової кореляції? Значення 5,61% вказує на слабку позитивну кореляцію, що свідчить про те, що змінні є відносно незалежними.


